title: 12金币
date: 2023-05-16 11:42:26
tags: 数据结构与算法
-
git地址:https://github.com/944613709/HIT-Data-Structures-and-Algorithms
-
12金币
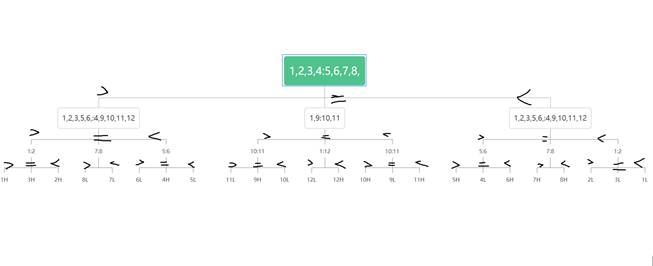
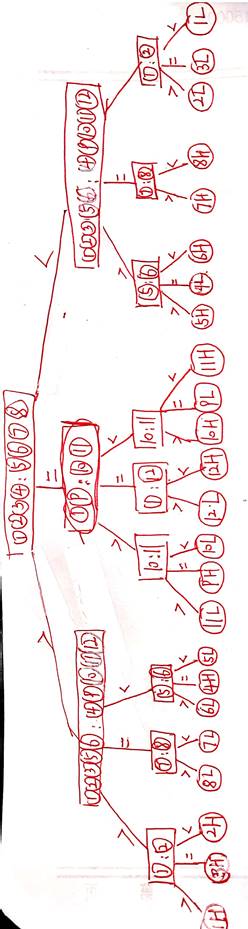
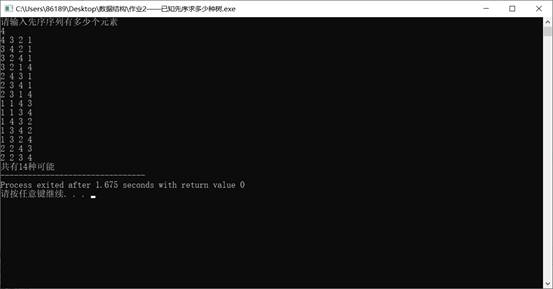
**问题:**给出12个硬币,其中一个是假硬币,用一个天平来确定三种重量的假币(其中假币可能比其他硬币轻或重)。问:至少称量多少次能够保证判断出:是否假币,而且如果有,确定假币是哪一颗,
算法思想:
首先将金币分成三份,然后取出前面两份进行比较,第一次比较之后能够缩小假币的范围以及能够确定某些一定是真币,第二次就可以缩小范围以及利用已经确定是真币的去进行比较,第二次比较之后能够进一步缩小范围,第三次再次利用小范围可能的假币和已知的真币的信息进行比较,从而确定假币
算法步骤:
\1. 分为三份A 1,2,3,4 B 5,6,7,8, C 9,10,11,12
(1) A=B -》A和B全真,假币在C
① 分为D 1,9 E 10,11
\1) D=E ——》可能情况:12L12H
a. 1>12 12L
b. 1<12 12H
\2) D>E ——》可能情况:9H11L10L
a. 10=11 9H
b. 10>11 11L
c. 10<11 10L
\3) D<E ——》可能情况:9L10H11H
a. 10=11 9L
b. 10>11 10H
c. 10<11 11H
(2) A>B——》 C全真
① 分为F 1,2,3,5,6 G 4,9,10,11,12
\1) F=G——》可能情况:8L7L
a. 7>8 8L
b. 7<8 7L
\2) F>G——》可能情况:3H1H2H
a. 1=2 3H
b. 1>2 1H
c. 1<2 2H
\3) F<G——》可能情况:4H6L5L
a. 5=6 4H
b. 5>6 6L
c. 5<6 5L
(3) A<B——》C全真
① 分为 H 1,2,3,5,6, I 4,9,10,11,12
\1) H=I——》可能情况:7H8H
a. 7>8 7H
b. 7<8 8H
\2) H>I——》可能情况:4L5H6H
a. 5=6 4L
b. 5>6 5H
c. 5<6 6H
\3) H<I——》可能情况:3L2L1L
a. 1=2 3L
b. 1>2 2L
c. 1<2 1L
判定树图