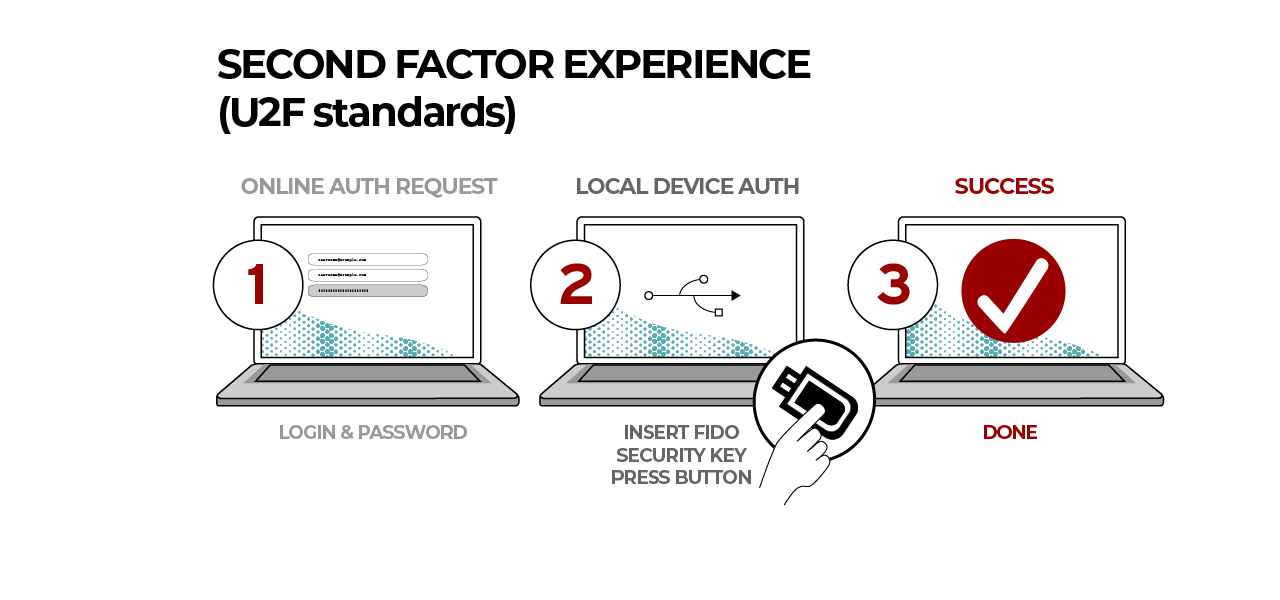
本篇要分享的内容是带头双向链表，以下为本片目录

一、链表的所有结构

二、带头双向链表

2.1尾部插入

2.2哨兵位的初始化

2.3头部插入

2.4 打印链表

2.5尾部删除

2.6头部删除

2.7查找结点

2.8任意位置插入

2.9任意位置删除

在刚开始接触链表的时候，我们所学仅仅所学的是单链表，相信大家用C语言学习单链表时也倍受二级指针的折磨。当然单链表只是链表结构内的一种，他的结构非常简单，但是理解并操作起来却非常困难；而我们今天要研究的是链表中结构最复杂，但是理解起来最简单的链表的结构。

一、链表的所有结构

在学习带头双向链表之前先了解一下链表的所有结构

1.单向或双向

2.带头或不带头

3.循环或不循环

还可以将以上的链表结构进行组合

最终链表有八种结构。

这里要说明的是带头和不带头的情况，这里的头意思就是哨兵位，哨兵位也就是作为链表的开头链接后面的数据，但是不存放任何数据，需要单独开辟一个结点来确定哨兵位，这就是带头不带头的意思。

二、带头双向链表

其实我们也没有必要一个一个的去了解那么多的链表结构，我们平时用到的最多的还是两个结构

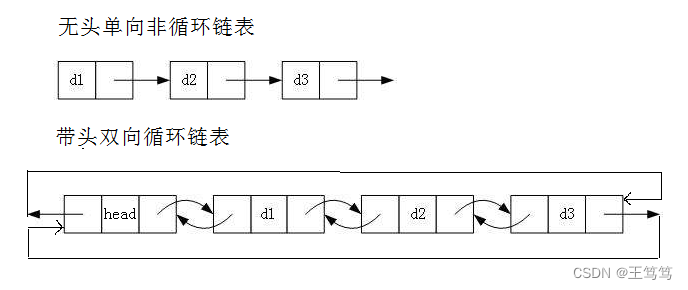
1. 无头单向非循环链表：结构简单，一般不会单独用来存数据。实际中更多是作为其他数据结
构的子结构，如哈希桶、图的邻接表等等。另外这种结构在笔试面试中出现很多。
2. 带头双向循环链表：结构最复杂，一般用在单独存储数据。实际中使用的链表数据结构，都
是带头双向循环链表。另外这个结构虽然结构复杂，但是使用代码实现以后会发现结构会带
来很多优势，实现反而简单了，后面我们代码实现了就知道了。

2.1尾部插入

和单链表相同，我们同样掌握带头循环链表的增删查改，但是带头循环链表的增删查改会比单链表容易许多。

首先定义一个结构体来存放前一个结点的位置和后一个结点的位置和数据；

typedef int LTDataType;
typedef struct ListNode
{
	struct ListNode* prev;
	struct ListNode* next;
	LTDataType Data;
}LTNode;

接下来画图给大家演示一下

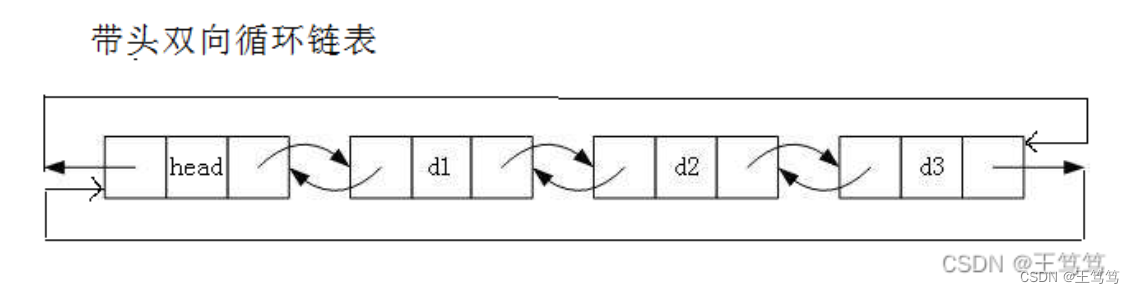
这里要插入的是newnode这个结点，我们可以直接操作phead的prev来实现尾插。

和单链表的尾插相同的，尾插就得先找尾，这个链表结构中的找尾，只需要通过phead的prev即可找到尾，比单链表中的找尾要方便许多。

插入newnode也非常简单，只需要改变四个指针的位置即可，以下是尾部插入的代码

void PushBack(LTNode* phead, LTDataType x)
{
	assert(phead);
	LTNode* tail = phead->prev;
	LTNode* newnode = BuyLTNode(x);
	tail->next = newnode;
	newnode->prev = tail;
	newnode->next = phead;
	phead->prev = newnode;
}

在对比一下以上两幅图和尾插的代码，首先写出一个开辟节点的代码用来开辟newnode（放在后面说）。

newnode已经开辟好，然后改变四个指针的方向；

先让哨兵位phead通过prev来找尾，令尾为tail；

让tail的next来指向新的结点newnode；

再让新结点newnode的prev链接上一个结点tail；

再让新节点newnode的next重新指向哨兵位；

最后让哨兵位phead的prev指向新节点newnode；这样newnode才能成为链表的尾结点；

这样就是一个完整的尾插；

兄弟萌，对比单链表的尾插，在逻辑上带头循环链表的尾插是要简单一些，一目了然。

2.2哨兵位的初始化

那为什么可以这么这么简单呢？

如下图

可以看到我们对哨兵位的初始化，如果链表为空时，phead的prev就指向自己，phead的next也可以指向自己，这就是对哨兵位的初始化

LTNode* LTInit()
{
	LTNode* phead = BuyLTNode(-1);
	phead->next = phead;
	phead->prev = phead;
	return phead;
}

2.3头部插入

既然都是插入我们不妨大胆猜测一下，他是否和尾插一样呢？

接下来继续画图分析：

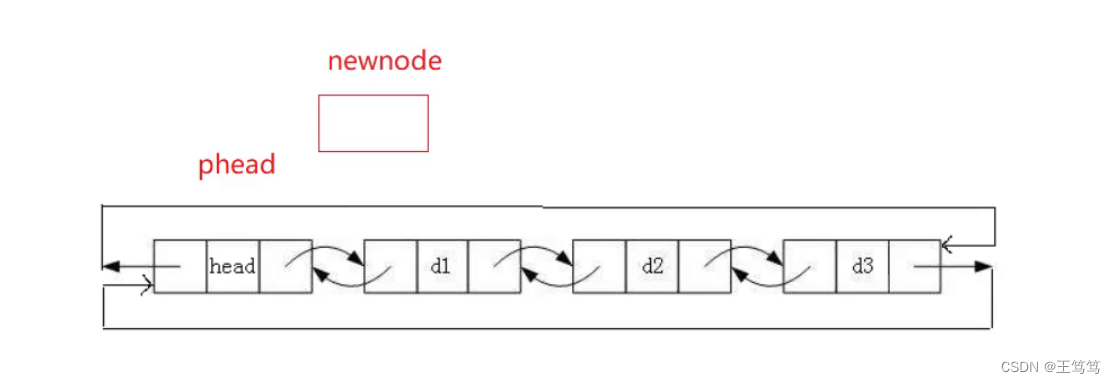头插要注意的是要插入到哨兵位之后，因为我们需要通过哨兵位来找到这个链表，所以要在哨兵位后面插入，也就是头插。

同样的上图先malloc了一个结点出来，那如何处理这个结点呢？

假设我们和尾插一样，先处理这个结点前面的指针

让phead的next指向newnode；

让newnode的prev指向phead；

再让newnode的next指向下一个结点；

这样做真的可以做到吗？

当然是不行的啦；

你有没有发现，如果我们先改变phead的next，令他指向newnode的话，它还可以找到newnode的下一个结点吗？显然是不行的，所以在头部插入时我们需要先改变newnode后面的结点，让newnode先和后面的结点链接起来，再让他和前面的结点进行连接，这样才是头插的正确用法。

下面是头插的代码

void PushFront(LTNode* phead, LTDataType x)
{
	assert(phead);
	LTNode* newnode= BuyLTNode(x);

	newnode->next = phead->next;
	phead->next->prev = newnode;
	phead->next = newnode;
	newnode->prev = phead;

}

可以对照上图仔细阅读一下代码，应该不难看懂；

2.4 打印链表

既然我们上面讨论过头插和尾插，我们不妨将其输出验证一下结果

void LTPrint(LTNode* phead)
{
	assert(phead);
	printf("sentinel bit<==>");
	LTNode* cur = phead->next;
	while (cur != phead)
	{
		printf("%d<==>", cur->Data);
		cur = cur->next;
	}
	printf("\n");
}

sentinel是哨兵位的意思，我们要通过哨兵位才能找到这些链表；

我们先定义一个新的结构体指针cur，让cur指向头节点的下一个结点，向后迭代，通过cur来遍历这个链表，简单来说就是从哨兵位后面的那个结点开始遍历，当这个结点知道下一个是哨兵位的时候结束了。

那结合上面的图示我们可以知道phead的next走到最后就会又回到phead的位置，所以我们不妨让cur=phead成为循环结束的标志，当cur!=phead 的时候就打印链表内容

我们应用上面的两个插入函数来验证

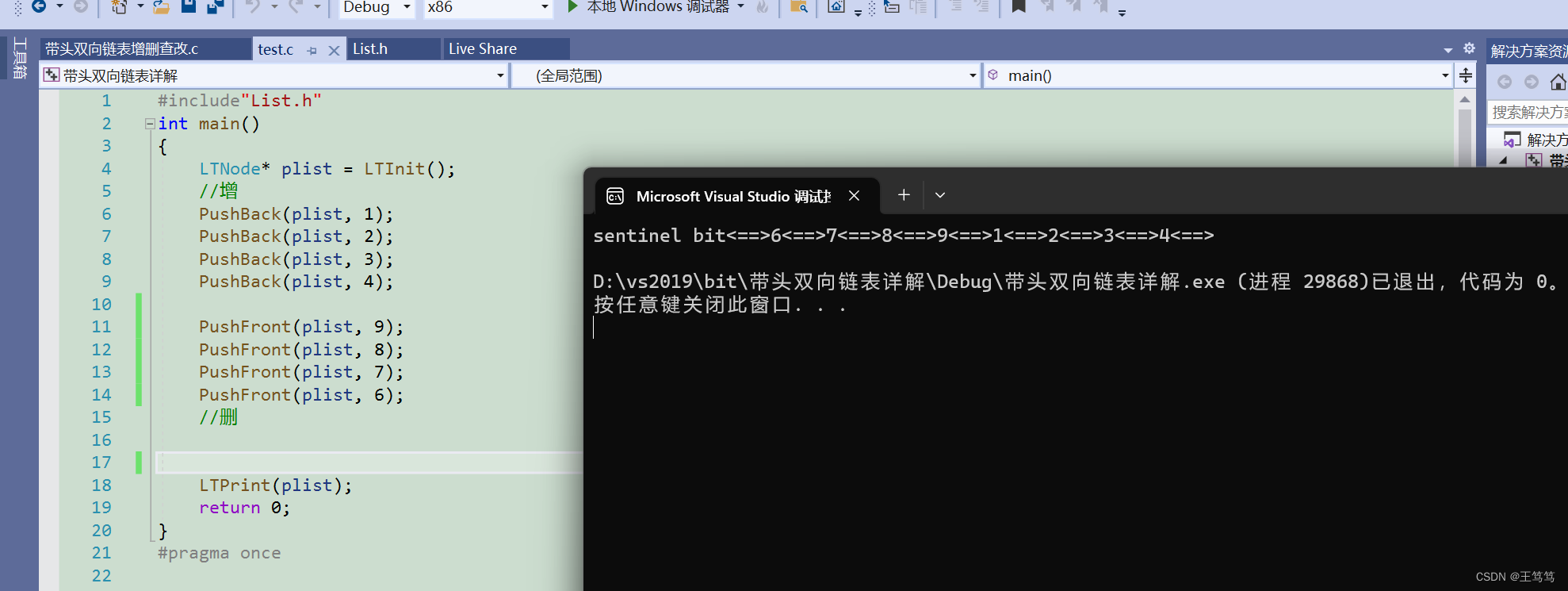
可以看到我们的头部插入和尾部插入，还有打印函数都非常的成功。

2.5尾部删除

我们不妨先看看单链表的尾部删除

可以看到步骤是相当的繁琐，因为不仅要找尾，还要判空，还要判断是否只有一个数据，非常非常的麻烦，可以说是集各种缺点于一身。

但是带头双向链表的尾部删除写起来非常爽

再继续画图来理解

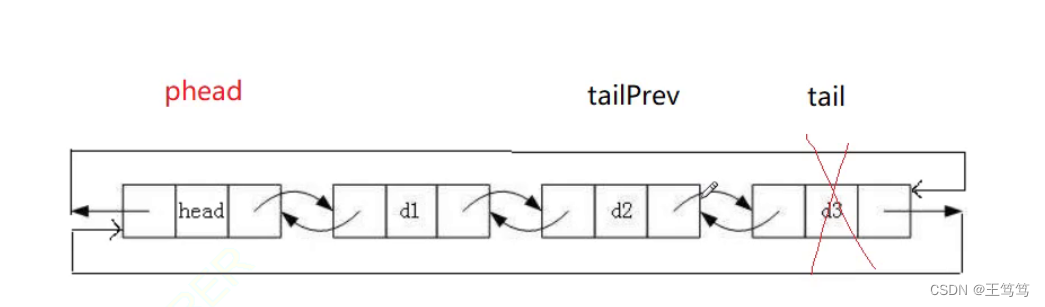
带头双向链表的尾删只要通过phead的prev就可以找到尾结点tail，并且找到尾结点tail后可以继续通过tail->prev来找到tail的前一个结点，我们将他成为tailPrev

然后将phead的prev指向tailPrev这个结点；

再将tailPrev这个结点的next指向phead哨兵位，这样就把tail孤立出去了，此时tailPrev就成为了新的尾结点

最后再将tail用free释放掉就就可以达到尾删的结果

以下是代码

void PopBack(LTNode* phead)
{
	assert(phead);
	assert(!LTEmpty(phead));
	LTNode* tail = phead->prev;
	LTNode* tailprev = tail->prev;
	free(tail);

	tailprev->next = phead;
	phead->prev = tailprev;
}

可以对照着上面的图和文字步骤仔细理解一下代码的内容，应该不难看懂。

2.6头部删除

既然是头部删除，那就继续要在哨兵位上动手脚，我们继续来画图理解

相信这个图也很清晰了，通过哨兵位phead找到下一个结点的next，也就是next的next，然后free掉next来达到删除的效果，再让原先next的next的prev来指向哨兵位，这样第二个结点就代替了第一个结点达到头部删除的效果，下面是代码

void PopFront(LTNode* phead)
{
	assert(phead);
	assert(!LTEmpty(phead));
	LTNode* first = phead->next;
	LTNode* second = first->next;

	phead->next = second;
	second->prev = phead;

	free(first);

}

我们不妨将phead->next定义为first，将next->next定义位second，这样代码的可读性就会大大提高，将代码对照以上文字描述和图片仔细理解，应该不难看懂。

当然在增强代码可读性方面还需要做的一点就是assert的断言；可以看到上面的代码中出现了

assert(!LTEmpty(phead));

这样一串代码中assert怎么断言一个函数呢？那这是什么意思呢？

我们用bool写一个函数

bool LTEmpty(LTNode* phead)
{
	assert(phead);
	return phead->next == phead;
}

意思就是说如果链表中没有元素了，phead的next还是等于phead的话就说明链表已经空了，这样做的好处就是可以提醒你链表中已经没有元素来让你删除了，从而达到暴力检查让编译器报错的效果。

我们在主函数中使用以下我们上面所写的删除函数

可以看到我们的尾部删除已经删掉了尾部插入的4，那我们再多次使用删除函数会怎样

可以看到再main函数中直插入了四个数据，但是却使用了五次删除函数，运行时就会报错，而报错的内容就是我们刚刚写的布尔函数，它可以大大加强代码的可读性。

2.7查找结点

查找结点再带头双向循环列表中也不困难，同样的是要对链表进行遍历查找。我们要查找的是结点，所以定义函数类型的时候一定是结构体指针类型，找到了就返回他的结点，找不到就返回空，这就是大体思路

LTNode* LTFind(LTNode* phead, LTDataType x)
{
	assert(phead);
	LTNode* cur = phead->next;
	while (cur != phead)
	{
		if (cur->Data == x)
		{
			return cur;
		}
		cur = cur->next;
	}
	return NULL;

}

这里就需要传两个参数了，一个是链表的头节点以便于我们找到链表并遍历查找，另一个就是我们想要找的数x。

当然也需要重新定一个结构体指针来遍历数组，并且和打印函数的循环条件相同，当检测到下一个结点时哨兵位phead的时候就停止循环了，因为下一个结点是phead的时候已经遍历完整个链表了。

这时就要操作结构体中的数据Data了，如果遍历时结点中的数据Data等于我们传入的参数x，那么就烦回这个结点，如果没有找到就返回空。

其实查找函数可以和其他的函数嵌套使用，因为查找函数返回的是结构体指针类型，而其它函数的参数也是结构体指针类型，我们可以将其和插入函数和删除函数一起使用。

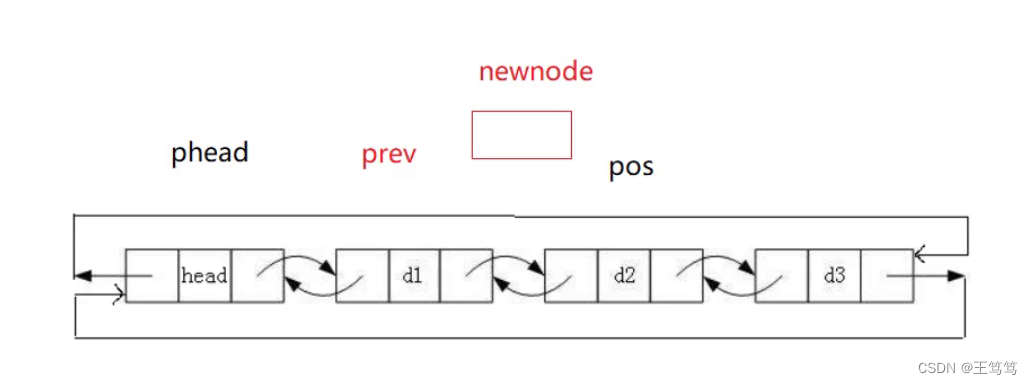
2.8任意位置插入

和其他的插入方法一样的只需要改变指针的指向的内容即可。

以下是图例

void LTInsert(LTNode* pos, LTDataType x)
{
	assert(pos);

	LTNode* prev = pos->prev;
	LTNode* newnode = BuyLTNode(x);

	prev->next = newnode;
	newnode->prev = prev;

	newnode->next = pos;
	pos->prev = newnode;
}

中间插入就不需要再使用phead了，因为phead是哨兵位，而中间插入需要的是其他的结点，也就是通过刚刚讨论过的查找函数所查找出来的结点，你就会发现，查找函数和其他函数就这样连接在一起了。

首先定义一个结构体指针prev来存放查找出来的那个结点的前面一个结点；

然后开辟一个新的结点newnode；

然后就和尾插一模一样的方法改变指针指向的内容即可。

也可以在main函数中使用验证一下

这里的意思就是通过查找函数找到3的位置，并且再3的前面插入30，验证正确；

2.9任意位置删除

同样的也需要通过查找函数来确定删除的位置，以下是图例

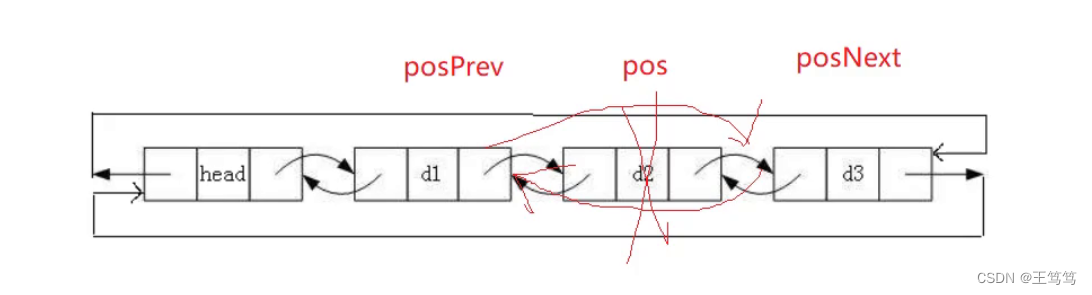
仔细研究完头部删除和尾部删除的内容应该不难看懂。

首先要找到pos前面的一个结点和后面的一个结点，然后直接将前一个结点的next指向pos的下一个结点；

将pos的下一个结点的prev指向pos的上一个结点；

最后再free掉pos这个位置即可完成删除操作；

以下是任意位置删除的代码

void LTErase(LTNode* pos)
{
	assert(pos);
	LTNode* posPrev = pos->prev;
	LTNode* posNext = pos->next;

	posPrev->next = posNext;
	posNext->prev = posPrev;
	free(pos);
	;
}

继续再mian函数中使用

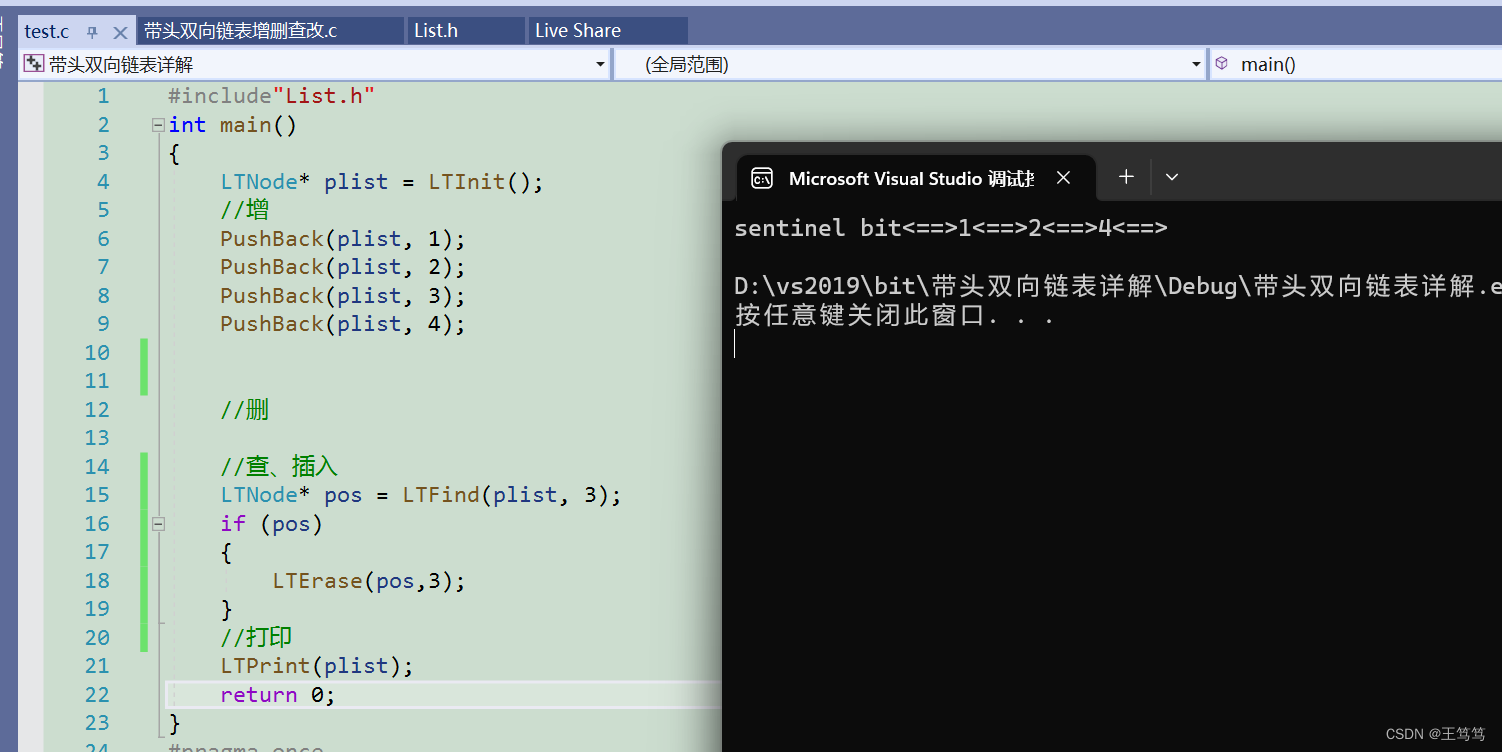可以看到3就被删除掉了。