1. 简介

• n8n是一款强大的工作流程自动化工具，可以自定义想要使用的功能和应用程序。n8n基于节点能够将任何工具连接在一起，轻松部署不同类型的任务。
• n8n虽然在国内知名度没那么高，但是老外确实非常喜欢这个工具。我们简单搜索一下就可以发现
• 知乎上基本上没有人讨论这个话题，就算仅有的几个回答也是好多年之前的，不知道的人还以为是一个小众软件呢
• 

B站上面更是直接搜索不到

• 

• 但是当你打开它的GitHub页面，发现上面的star达到了30K，这是非常恐怖的一个数字
• 

2. 安装

2.1. 使用npx进行安装

npx n8n

这个方法可能有坑就不做过多介绍了

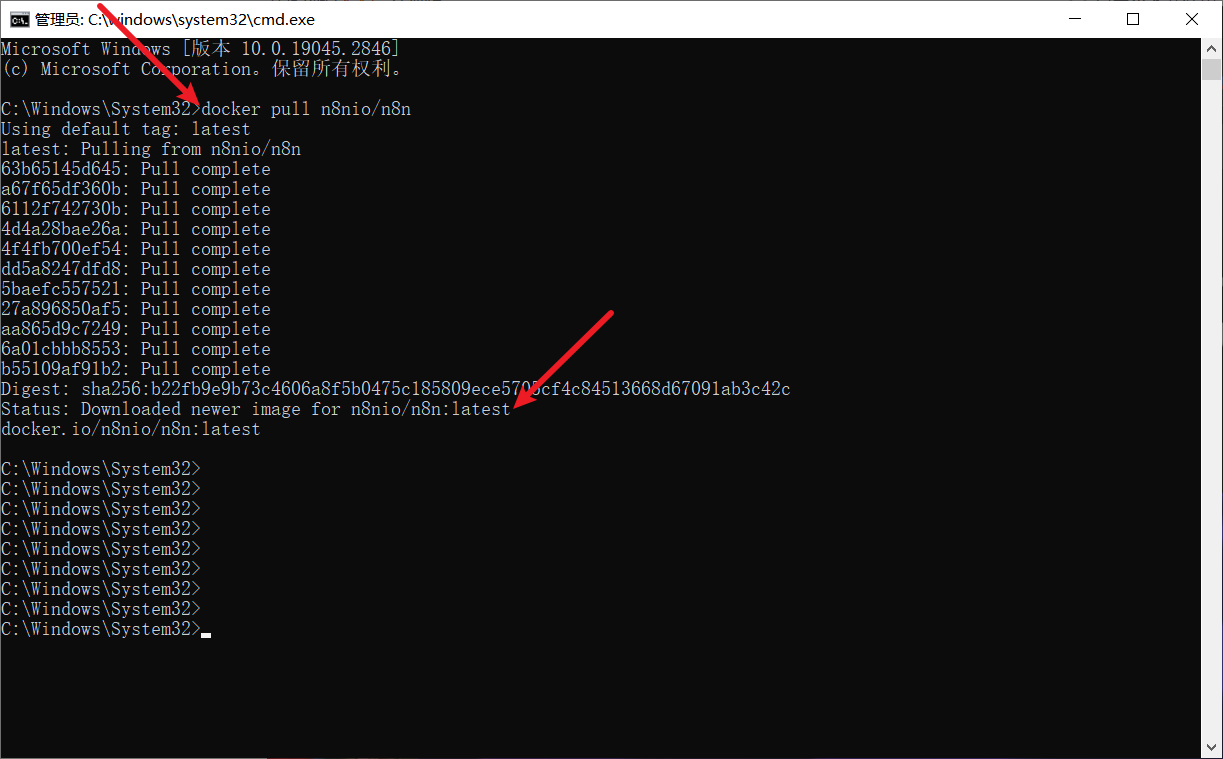
2.2. 使用docker进行安装

• 在docker中搜索n8nio/n8n
• Docker
• 
• 

• 使用下面的代码进行安装
• docker pull n8nio/n8n
• 

2.3. 设置端口（可选）

• 默认的端口使用的是5678，但是如果和某些软件的端口有所冲突，可以对其进行修改
  

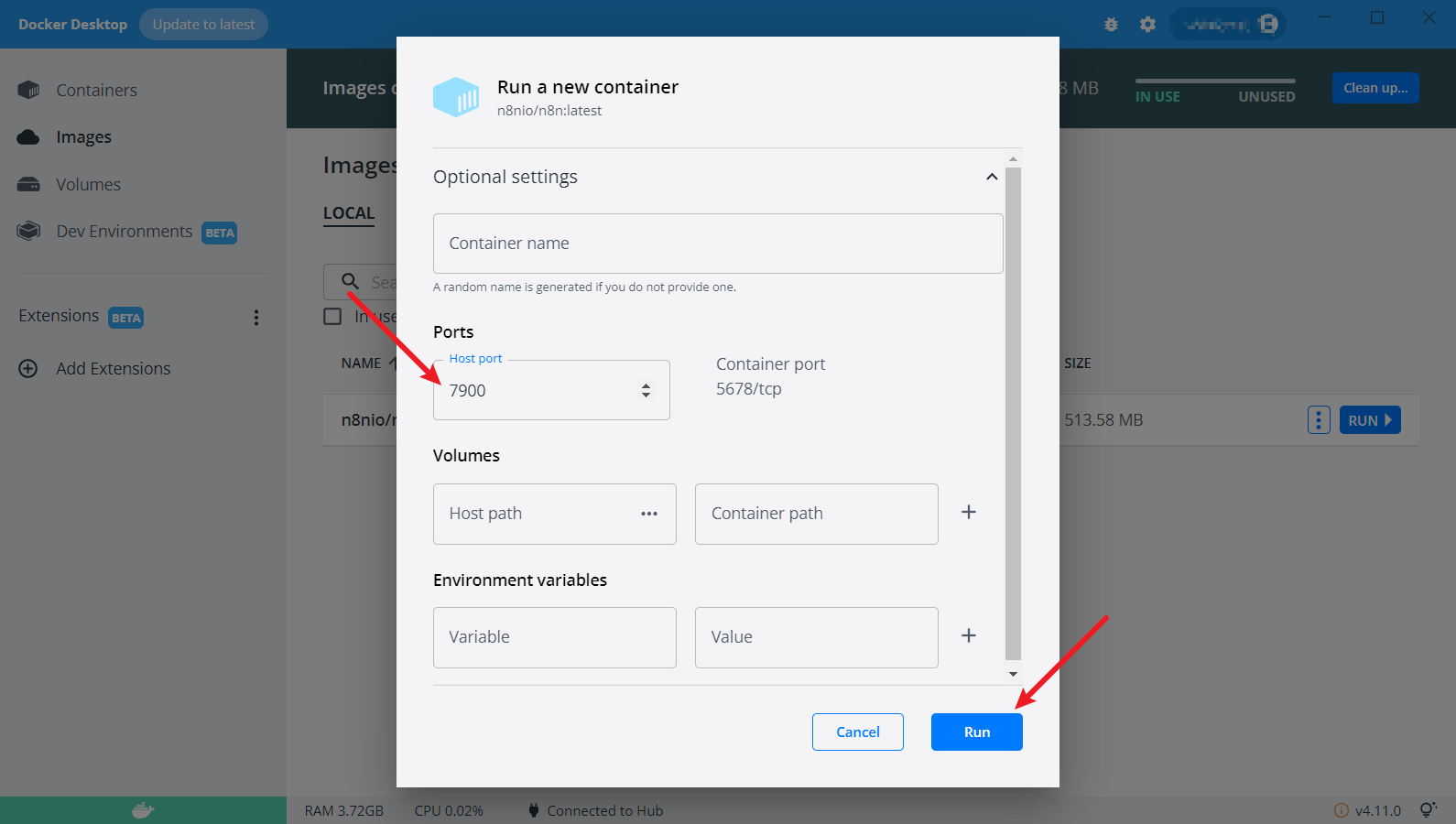
• 修改完端口之后打开下面的网址，可以查看到n8n对应的工作页面
  默认的5678端口

• 127.0.0.1:5678/
  修改后的端口

• 127.0.0.1:7900/

http://127.0.0.1:7900/

3. 登录

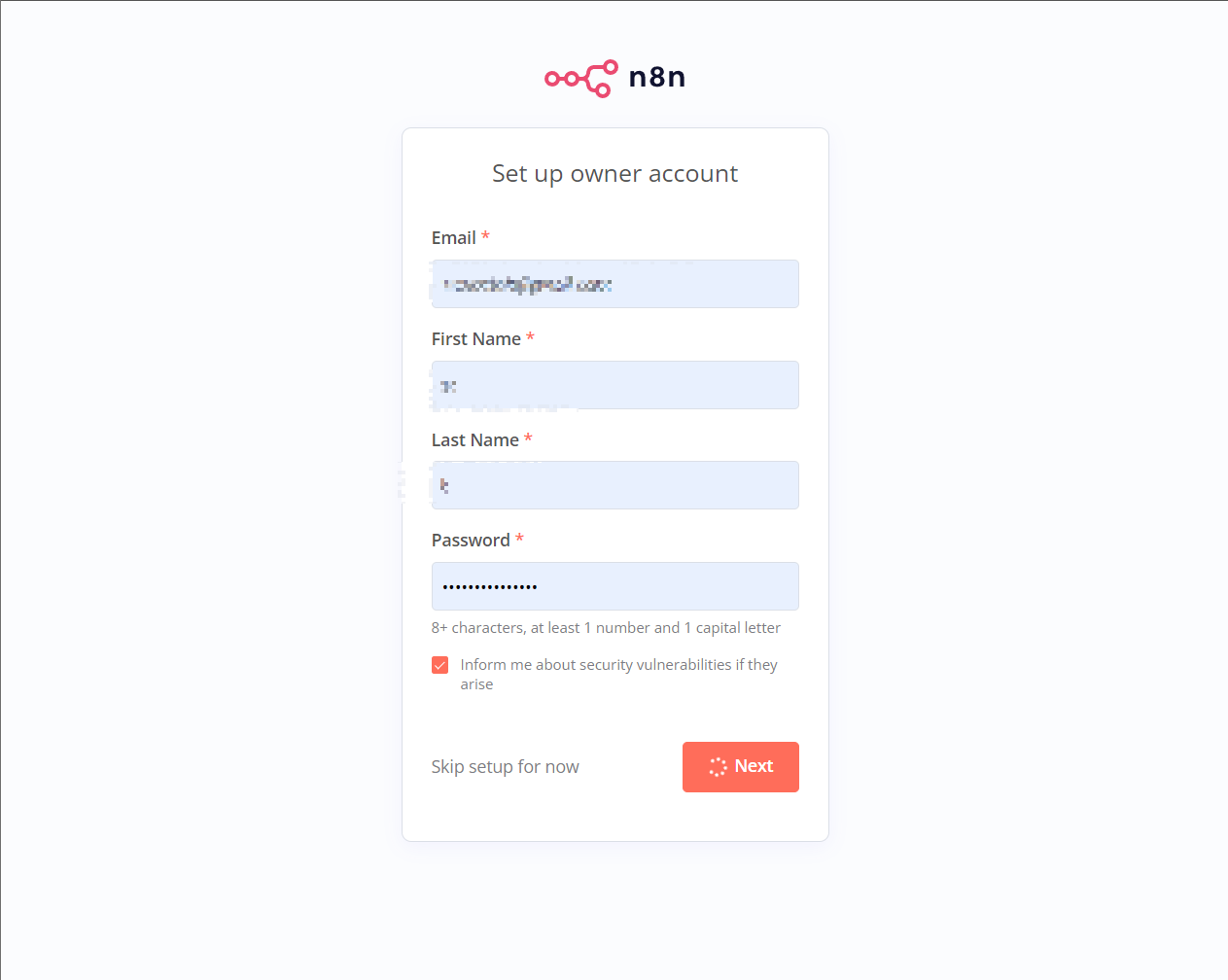
• 第一次打开的时候需要注册对应的账号，也可以先跳过去之后再登录
  

• 我这里会避免后续功能被限制，所以直接注册了一个账号进行了登录
  

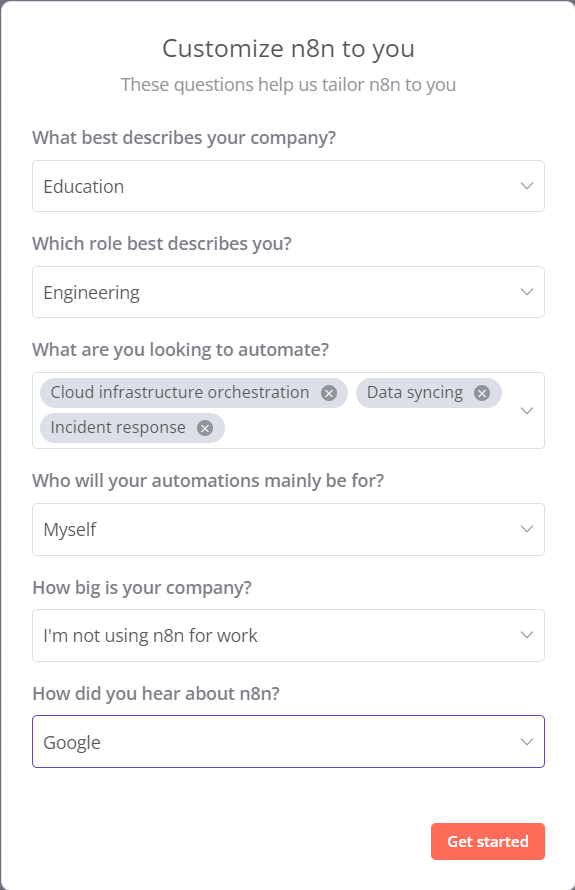
• 之后再随便填一下，自己使用n8n的目的
  

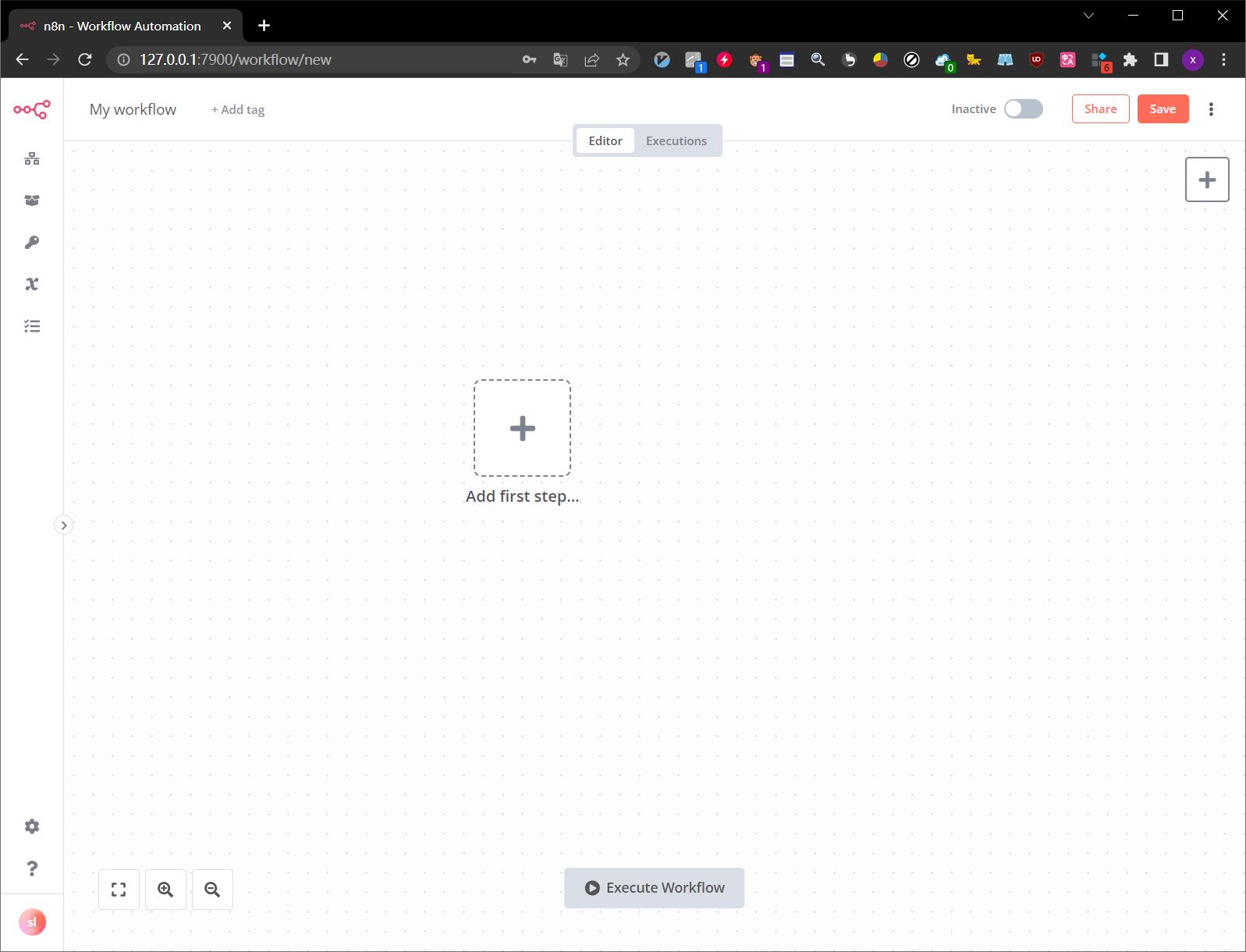
• 就可以最终进入到n8n的工作界面了
  如下所示，需要什么样的工作流就拖对应的模块进行组合即可
  

4. 搜索工作流

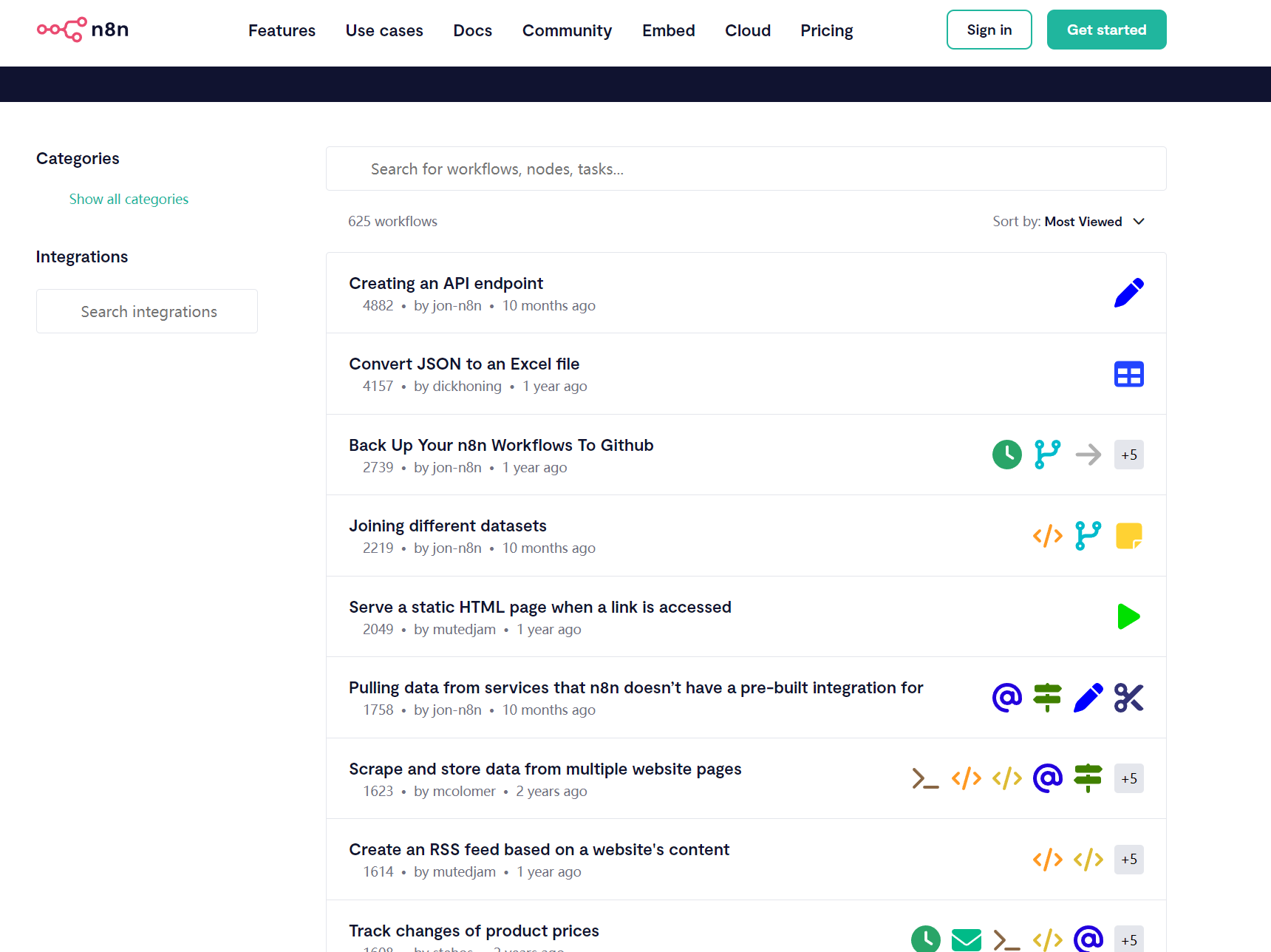
• 在官网的工作流市场中，我们可以到找到大量现成的n8n工作流。当然了，这些主要是面向国外人的工作流的。在国内很多我们都用不了
• n8n workflow templates
•