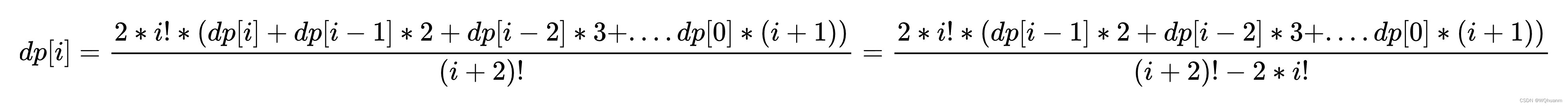题目

严老师和宋老板去勘测武威市区的道路网，每一条路都需要勘测，且需要两人合作.武威市区可以近似地看成六横六纵组成的道路网，自西向东依次为学府路、民勤路、西关路、中关路、富民路、滨河路；自北向南依次为雷海路、宣武路、祁连大道、商业街、南关路、古浪街，任意两个相邻的路口之间的间距均可以认为是500米。
初始时，严老师和宋老板在民勤路与商业街相交的十字路口，最终仍然需要回到这个位置，则他俩至少需要走多少千米?并设计一条路线。

解析

题目对应的图。
在这里插入图片描述
本题是找欧拉回路。路径可以重复走，节点可以重复访问。
由于本题的权是相同的，都是 $500 m$ ，因此本题节点虽然多，但是难度降低很多。

求解过程

统计图中点度数

$v_{11}$ 的度数为 $2$ 。
$v_{12}$ 的度数为 $3$ 。
$v_{13}$ 的度数为 $3$ 。
$v_{14}$ 的度数为 $3$ 。
$v_{15}$ 的度数为 $3$ 。
$v_{16}$ 的度数为 $2$ 。
$v_{21}$ 的度数为 $3$ 。
$v_{22}$ 的度数为 $4$ 。
$v_{23}$ 的度数为 $4$ 。
$v_{24}$ 的度数为 $4$ 。
$v_{25}$ 的度数为 $4$ 。
$v_{26}$ 的度数为 $3$ 。
$v_{31}$ 的度数为 $3$ 。
$v_{32}$ 的度数为 $4$ 。
$v_{33}$ 的度数为 $4$ 。
$v_{34}$ 的度数为 $4$ 。
$v_{35}$ 的度数为 $4$ 。
$v_{36}$ 的度数为 $3$ 。
$v_{41}$ 的度数为 $3$ 。
$v_{42}$ 的度数为 $4$ 。
$v_{43}$ 的度数为 $4$ 。
$v_{44}$ 的度数为 $4$ 。
$v_{45}$ 的度数为 $4$ 。
$v_{46}$ 的度数为 $3$ 。
$v_{51}$ 的度数为 $3$ 。
$v_{52}$ 的度数为 $4$ 。
$v_{53}$ 的度数为 $4$ 。
$v_{54}$ 的度数为 $4$ 。
$v_{55}$ 的度数为 $4$ 。
$v_{56}$ 的度数为 $3$ 。
$v_{61}$ 的度数为 $2$ 。
$v_{62}$ 的度数为 $3$ 。
$v_{63}$ 的度数为 $3$ 。
$v_{64}$ 的度数为 $3$ 。
$v_{65}$ 的度数为 $3$ 。
$v_{66}$ 的度数为 $2$ 。

配对

图中，奇点有： $v_{12},v_{13},v_{14},v_{15},v_{21},v_{26},v_{31},\\v_{36},v_{41},v_{46},v_{51},v_{56},v_{62},v_{63},v_{64},v_{65}$ ，合计 $16$ 个。
把他们配对，枚举所有配对，找到代价最小的配对。
由于本题的权值相同，因此，最小配对为 $v_{12},v_{13}),(v_{14},v_{15})(v_{21},v_{31}),(v_{26},v_{36}),\\(v_{41},v_{51}),(v_{46},v_{56}),(v_{62},v_{63}),(v_{64},v_{65})$ 。

添加重边，去掉奇点

如下图所示，红色为添加的边。
在这里插入图片描述
这样，新图中没有奇点，是一个欧拉图。
注意，将原来图中节点编号按照顺序进行修改，主要是为了计算机编程方便。

答案

最短路径

最短距离 $(60 + 8) * 500 = 34, 000 m$ ，其中 $60$ 为原有路径， $8$ 为构造欧拉图增加的路径。

方案

$10\to 4\to 3\to 2\to 1\to 7\to 8\to 2\to 3\to 9\to 8\to 14\to\\ 13\to 7\to 13\to 19\to 20\to 14\to 15\to 9\to 10\to 11\to 5\to\\ 4\to 5\to 6\to 12\to 11\to 17\to 16\to 15\to 21\to 20\to 26\to\\ 25\to 19\to 25\to 31\to 32\to 26\to 27\to 21\to 22\to 23\to\\ 17\to 18\to 12\to 18\to 24\to 23\to 29\to 28\to 27\to 33\to 32\to\\ 33\to 34\to 35\to 29\to 30\to 24\to 30\to 36\to 35\to 34\to\\ 28\to 22\to 16\to 10$
注意：答案不唯一。

C++代码

#include<bits/stdc++.h>
using namespace std;

const int N=1e3+10;
int edge[N][N];
//为了方便优先访问编号小的节点，这里使用邻接矩阵来存边
//如果使用vector来存图，那还需要对每个节点连接的边进行排序
int ans[N*N];
int p=0;//ans指针 
int degree[N];//用于储存每个点的度，以求起点
int n;//节点数量 

void dfs(int now) {
    for (int i=1;i<=n;i++){//顺序寻找可访问的边，优先找编号小的节点
        if (edge[now][i]){//若这条边尚未访问过
            edge[now][i]--;//已访问过的边要删去，防止重复访问
            edge[i][now]--;//有向图的话请删去这一行
            dfs(i);
        }
    }
    ans[++p]=now;//将访问的节点储存进答案数组
    //由于递归的特性，这里储存的是逆序过程
}

int main() {
    ios::sync_with_stdio(false);
    int m;//边的个数
    cin>>n>>m;
    for(int i=1;i<=m;i++) {
        int a,b;
        cin>>a>>b>>c;
        edge[a][b]++;
        edge[b][a]++;//有向图的话删去这行
        degree[a]++;
		degree[b]++;//两个点的度都+1
    }
    int start;//起点 
    cin>>start;
    dfs(start);//dfs寻找欧拉路
    cout<<(p-1)*500<<"\n";//计算总代价 
    for(int i=p;i>=1;i--) {
        cout<<ans[i]<<" ";//输出给定的欧拉路
	}
    cout<<"\n";
    return 0; 
}

对应的测试数据如下。