创建面对象

QgsPolygon() #创建一个空的面
使用setExteriorRing设置多边形的外轮廓
使用addInteriorRing添加内部轮廓(洞)
QgsPolygon(exterior: QgsLineString, rings:Iterable[QgsLineString] = []) #使用外轮廓和内部的环
QgsPolygon(QgsPolygon) #复制一个多边形

def create_polygon_object():
    # 创建一条线
    line1 = QgsLineString([QgsPoint(0, 0), QgsPoint(1, 0), QgsPoint(1, 1), QgsPoint(0, 1)])
    showgeoms([line1], 'line1')

    # 使用setExterorRing
    polygon1 = QgsPolygon()
    polygon1.setExteriorRing(QgsLineString(line1))
    showgeoms([polygon1], 'polygon1')

    # 复制polygon
    polygon2 = QgsPolygon(polygon1)
    inring = QgsLineString([0.4, 0.6, 0.6, 0.4], [0.7, 0.7, 0.2, 0.2])
    polygon2.addInteriorRing(inring)  # 添加内部空洞
    showgeoms([polygon2], 'polygon2')
    return polygon2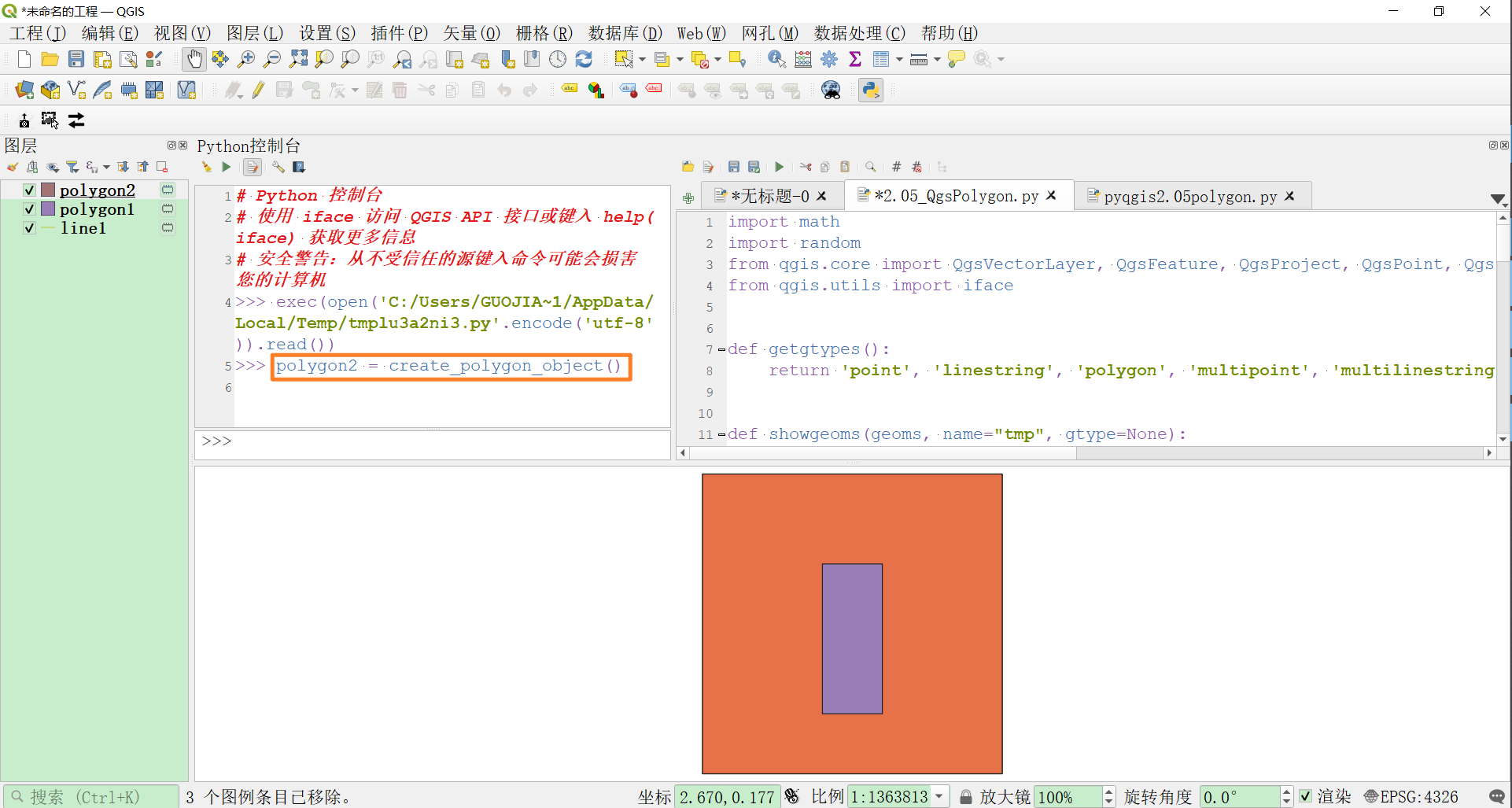

面对象的访问

访问外轮廓:
|3. exteriorRing() # 得到多边形的外轮廓
<QgsLineString: LineString (0 0，1 0, 1 1, 0 1, 0 0)>
访问内轮廓:
l3.numInteriorRings(） # 得到内轮廓的数量
l3.interiorRing(0) # 第1个内部轮廓，要小于numInteriorRings的数量

def access_surface_object(polygon2):
    polygon3 = polygon2.clone()  # 拷贝
    # 访问多边形的内外轮廓
    print(polygon3.exteriorRing())  # 外轮廓
    ering = polygon3.exteriorRing()
    showgeoms([ering], 'ering')

    print('内轮廓数量', polygon3.numInteriorRings())  # 内部轮廓的数量
    print(polygon3.interiorRing(0))  # 第1个内部轮廓，要小于numInteriorRings的数量
    inring = polygon3.interiorRing(0)
    showgeoms([inring], 'inring')

面对象的修改

moveVertex(QgsVertexld position, const QgsPoint &newPos) # 移动节点
insertVertex(QgsVertexld position, const QgsPoint &vertex) # 插入节点
deleteVertex(QgsVertexld position) # 删除节点

QgsVertexld类:表示要操作的节点。与线对象可以根据线的结点顺序进行定位不同，面有外轮廓，还可能有一个或多个内轮廓，这样定位某个点就比较复杂。因此构造了一个QgsVertexld类。

QgsVertexld是用于识别几何对象内唯一顶点的实用类。

QgsVertexId (int_ part=-1, int_ _ring=-1, int_ _vertex=-1, VertexType_type= SegmentVertex)

三个参数： _part 部分，_ ring 环，_ vertex 节点顺序

def QgsVertexld_1(polygon2):
    polygon2 = polygon2.clone()  # 拷贝
    # vertexid  part,  ring, vertex
    polygon2.partCount()  # 部分的数量
    polygon2.ringCount()  # 环的数量
    polygon2.nCoordinates()  # 整个对象的节点总数

    idx1 = QgsVertexId(3, 2, 1)
    print(idx1.isValid())
    print(idx1.isValid(polygon2))

    idx2 = QgsVertexId(0, 0, 1)
    print(idx2.isValid())
    print(idx2.isValid(polygon2))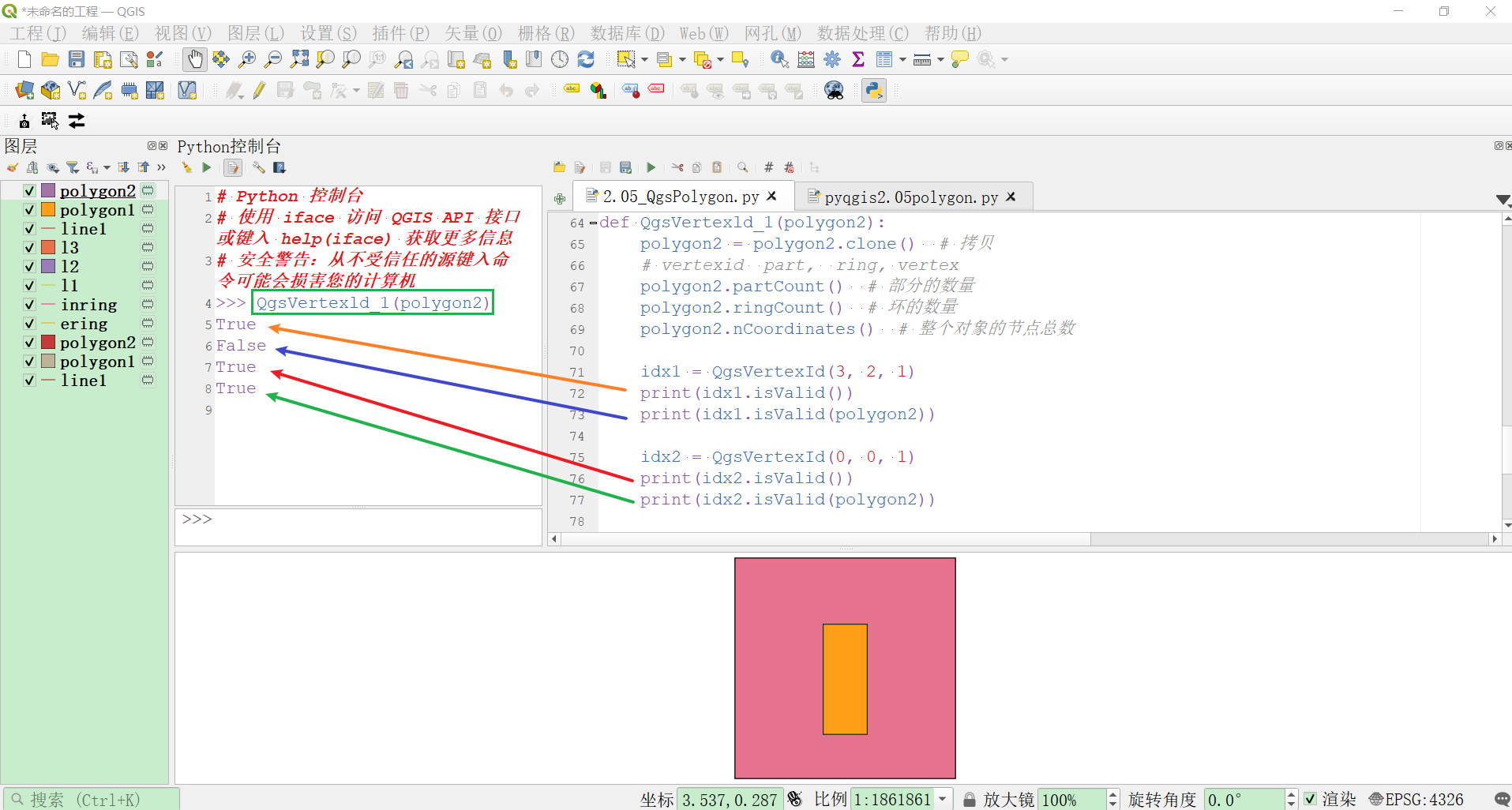

移动节点

def move_node(polygon2):
    idx2 = QgsVertexId(0, 0, 1)
    polygon2.moveVertex(idx2, QgsPoint(1, -0.5))  # 移动节点


移动前	移动后

插入节点

def insert_node(polygon2):  #插入节点
    idx2=QgsVertexId(0,0,1)
    polygon2.insertVertex(idx2,QgsPoint(0.5,-0.5))
    idx3=QgsVertexId(0,1,1)
    polygon2.insertVertex(idx3,QgsPoint(0.5,0.9))


插入节点前	插入节点后

删除节点

def delete_node(polygon2):#删除节点
    idx2=QgsVertexId(0,0,1)
    polygon2.deleteVertex(idx2)
    idx3=QgsVertexId(0,1,1)
    polygon2.deleteVertex(idx3)


删除节点前	删除节点后

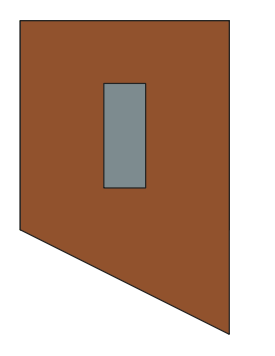
例子：生成经纬网

def generate_grid():
    polys = []
    for lon in range(0, 360, 10):
        for lat in range(-90, 90, 10):
            bottomleft = QgsPoint(lon, lat)
            bottomright = QgsPoint(lon + 10, lat)
            topright = QgsPoint(lon + 10, lat + 10)
            topleft = QgsPoint(lon, lat + 10)
            tl = QgsLineString([bottomleft, bottomright, topright, topleft])
            polys.append(QgsPolygon(tl))
    showgeoms(polys, 'grid')