每日一算-选择排序算法

news2024/11/24 1:55:20

大家好，我是易安！

今天我们开始每日一算的篇章，今天带来的是选择算法。

选择排序是一种简单而高效的排序算法，它通过从列表的未排序部分中重复选择最小（或最大）元素并将其移动到列表的已排序部分来工作。该算法反复从列表的未排序部分中选择最小（或最大）的元素，并将其与未排序部分的第一个元素交换。对列表中剩余的未排序部分重复此过程，直到整个列表排序完毕。选择排序的一种变体称为“双向选择排序”，它通过在最小元素和最大元素之间交替遍历元素列表，这种方式在某些情况下可以更快。

选择排序算法

该算法在给定数组中维护两个子数组。

已经排序的子数组。

剩余的子数组未排序。

在选择排序的每次迭代中，从未排序的子数组中选取最小元素（考虑升序）并将其移动到已排序子数组的开头。

每次迭代后，已排序的子数组大小增加一，未排序的子数组大小减少一。

在 N（数组的大小）次迭代之后，我们将得到一个排序的数组。

选择排序流程图：

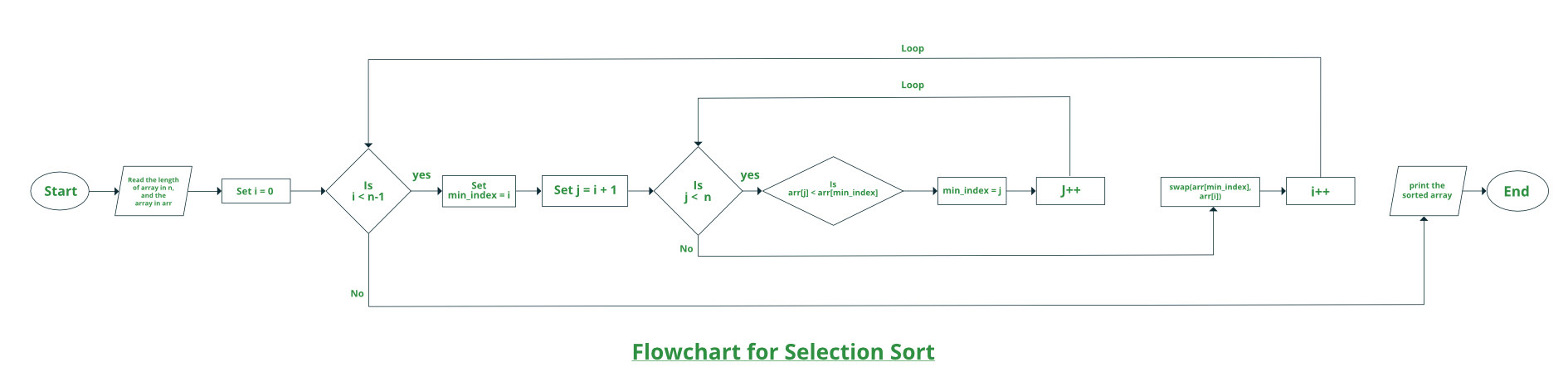
选择排序原理？

让我们以下面的数组为例：arr[] = {64, 25, 12, 22, 11}

第一步：

对于排序数组中的第一个位置，整个数组从索引 0 到 4 依次遍历。 当前存放64的第一个位置，遍历整个数组后显然 11是最低值。

64 25 12 22 11

因此，将 64 替换为11。经过一次迭代后，恰好是数组中最小值的 11 往往会出现在排序列表的第一个位置。

11 25 12 22 64

第二步：

对于存在 25 的第二个位置，再次按顺序遍历数组的其余部分。

11 25 12 22 64

遍历后发现 12是数组中倒数第二的值，应该出现在数组的第二位，因此交换这些值。

11 12 25 22 64

第三步：

现在，对于第三位，再次出现 25 的地方遍历数组的其余部分并找到数组中第三小的值。

11 12 25 22 64

遍历时， 22是第三小的值，它应该出现在数组的第三位，因此将 22与第三位的元素交换。

11 12 22 25 64

第四步：

同样，对于第四个位置，遍历数组的其余部分，找到数组中第四小的元素

由于 25是第四低的值，因此它将排在第四位。

11 12 22 25 64

第五步：

最后，数组中存在的最大值自动放置在数组的最后一个位置

结果数组是排序后的数组。

11 12 22 25 64

实战演练

请按照以下步骤实现代码：

将最小值 ( min_idx ) 初始化为位置 0。
遍历数组，找到数组中的最小元素。
在遍历时，如果找到任何小于 min_idx 的元素，则交换两个值。
然后，递增 min_idx以指向下一个元素。
重复直到数组被排序。

下面是上述方法的实现：

java版本

import java.io.*;
public class SelectionSort
{
 void sort(int arr[])
 {
  int n = arr.length;

  // 逐步移动未排序数组的边界
  for (int i = 0; i < n-1; i++)
  {
   //查找未排序数组中的最小元素
   int min_idx = i;
   for (int j = i+1; j < n; j++)
    if (arr[j] < arr[min_idx])
     min_idx = j;

   // 将找到的最小元素与第一个元素进行交换
   int temp = arr[min_idx];
   arr[min_idx] = arr[i];
   arr[i] = temp;
  }
 }

 // 打印排序后的数组结果
 void printArray(int arr[])
 {
  int n = arr.length;
  for (int i=0; i<n; ++i)
   System.out.print(arr[i]+" ");
  System.out.println();
 }


 public static void main(String args[])
 {
  SelectionSort ob = new SelectionSort();
  int arr[] = {64,25,12,22,11};
  ob.sort(arr);
  System.out.println("Sorted array");
  ob.printArray(arr);
 }
}