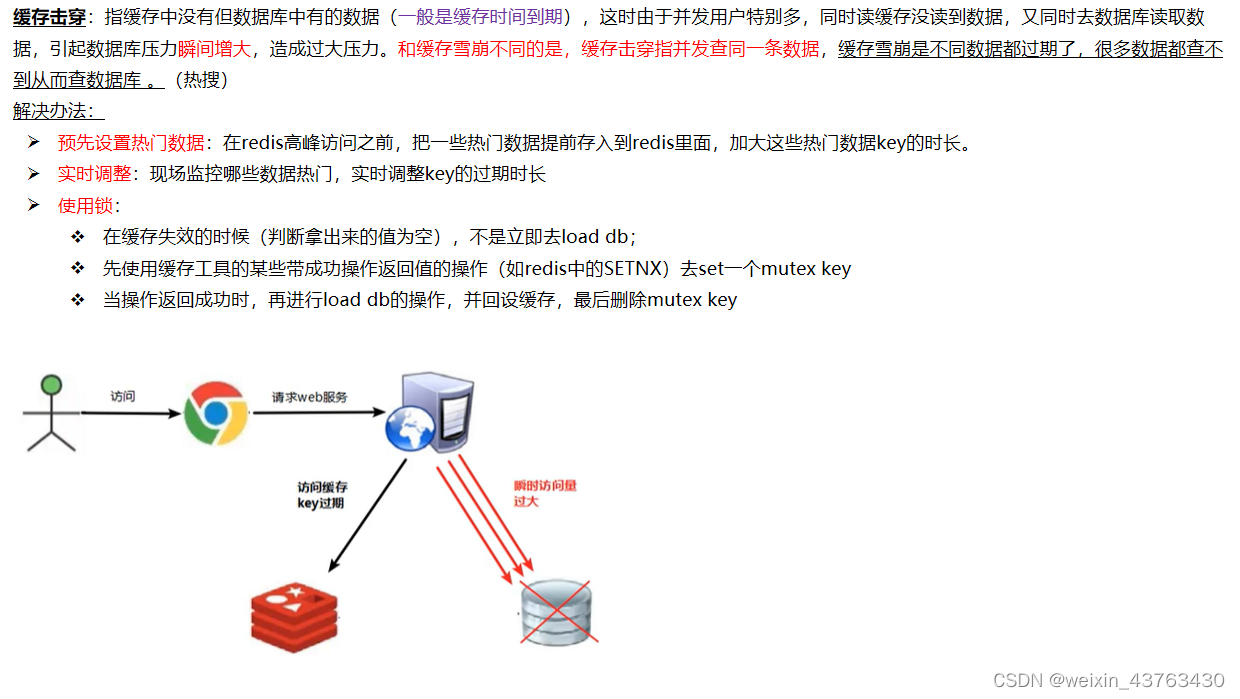
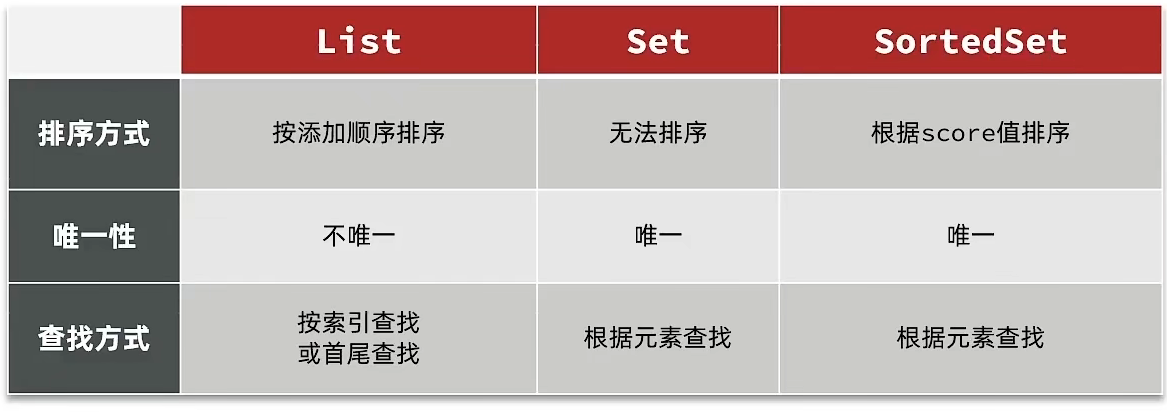
一、简介

梯度下降法（Gradient descent）或最速下降法（steepest descent）是求解无约束最优化问题的一种常用方法。

假设fx)在R上具有一阶连续偏导数的函数。要求解的无约束最优化问题是。其本质是一个迭代的方法，选择初始值x0，然后不断的迭代更新x0，进行目标函数的极小值，直到收敛结束。

二、案例分析

f(x,y)=(x^2+y^2)/2,迭代出最小值。、

步骤

1、设定出初始值x0 y0,步长L，以及收敛精度e

2、求函数f(x)的偏导数dx df

3、计算a=f(x0,y0),

x0=x0-L*dx(x,y);

y0=y0-L*dy(x,y)

b=f(x0,y0),

更新x0 y0

4、判断是否收敛 abs(a-b)>e ?返回3 开始循环：结束返回x0 y0

matlab代码：

% fun ：函数原型
% dx fun 的偏x导数
% dy fun 的偏y导数
% x0 y0初始值
% e 精度
% l 迭代步长 

% 
function [newX,newY,num_iterator,point] = Gradient_Descent(fun,dfunx,dfuny,x0,y0,e,l)
   value_a=feval(fun,x0,y0);
   % 开始计算第一次迭代
   % x_iterator=x-l*dx
   dx=feval(dfunx,x0,y0);
   newX=x0-l*dx;
   % 同理可以计算出新的y 
   dy=feval(dfuny,x0,y0);
   newY=y0-l*dy;
    % 开始计算第二次的值
    num_iterator=1;
    value_b=feval(fun,newX,newY);
    point(num_iterator,:) = [newX,newY,value_a];
    
    while(abs(value_a-value_b)>e)
       value_a=feval(fun,newY,newY);
      % x_iterator=x-l*dx
      dx=feval(dfunx,newX,newY);
      newX=newX-l*dx;
     % 同理可以计算出新的y 
      dy=feval(dfuny,newX,newY);
      newY=newY-l*dy;
      num_iterator=num_iterator+1;
      value_b=feval(fun,newX,newY);
      point(num_iterator,:) = [newX,newY,value_b];
    end
end

mian 函数：

% 目标函数为 z=f(x,y)=(x^2+y^2)/2
close all;
clear all;
clc
fun = inline('(x^2+y^2)/2','x','y');  % 函数(x^2+y^2)/2'
dfunx = inline('x','x','y');          %对x的导数
dfuny = inline('y','x','y');          %对y的导数
x0 = 3;               % 初始位置
y0 = 3;
Epsilon1 = 0.00000000001;   % 精度
Lambda1 = 0.01;        % 步长/更新率%求解
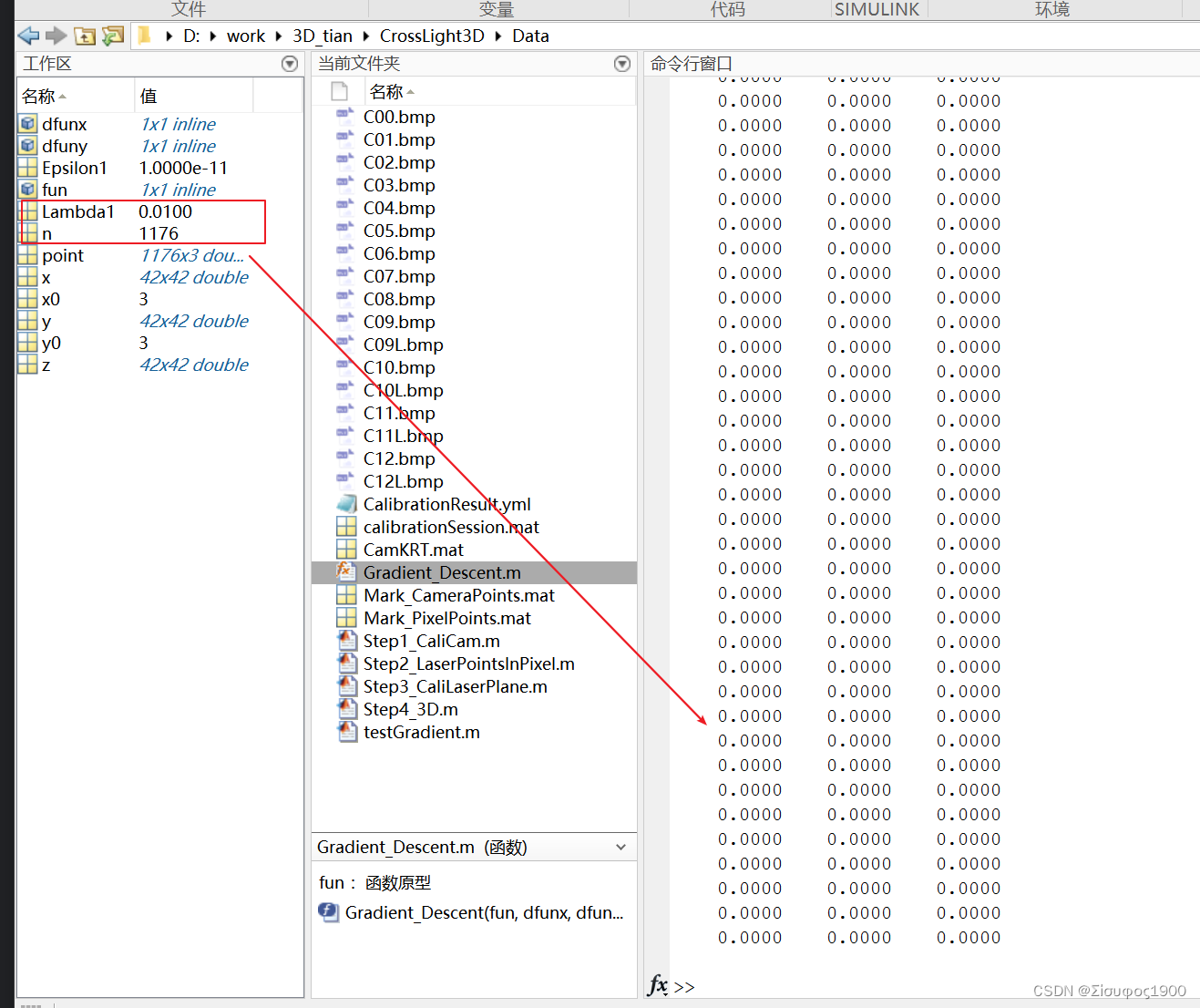
[x,y,n,point] = Gradient_Descent(fun,dfunx,dfuny,x0,y0,Epsilon1,Lambda1)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% figure 画图
x = -0.1:0.1:4;
y = x;
[x,y] = meshgrid(x,y);
z = (x.^2+y.^2)/2;
surf(x,y,z)    %绘制三维表面图形
xlabel('X');ylabel('Y');zlabel('z')% hold on
% plot3(point(:,1),point(:,2),point(:,3),'linewidth',1,'color','black')
hold on
scatter3(point(:,1),point(:,2),point(:,3),'r','*');