最长递增子序列

LeetCode 300. 最长递增子序列

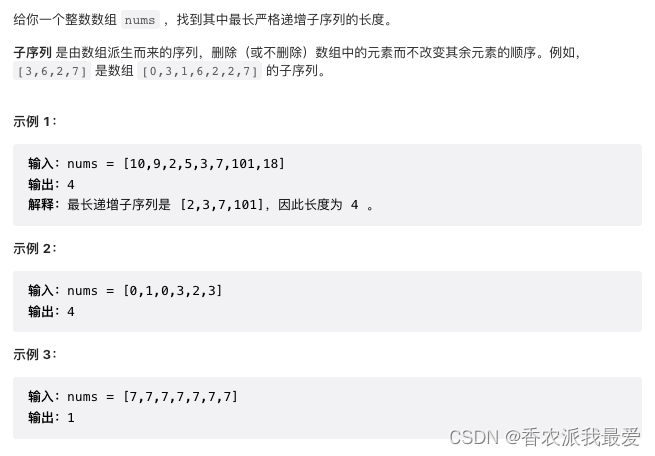
在这里插入图片描述

解题思路

dp[i]表示以nums[i]这个数结尾的最长递增子序列的长度。
我们已经知道了dp[0…4]的所有结果，我们如何通过这些已知结果推出dp[5]呢?
nums[5]前面有哪些元素小于nums[5]？这个好算，用 for 循环比较一波就能把这些元素找出来。

for (int i = 0; i < nums.length; i++) {
    for (int j = 0; j < i; j++) {
        // 寻找 nums[0..j-1] 中比 nums[i] 小的元素
        if (nums[i] > nums[j]) {
            // 把 nums[i] 接在后面，即可形成长度为 dp[j] + 1，
            // 且以 nums[i] 为结尾的递增子序列
            dp[i] = Math.max(dp[i], dp[j] + 1);
        }
    }
}

代码实现

class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);
        for(int i = 0;i < nums.length;i++){
            for(int j = 0;j < i;j++){
                if(nums[i] > nums[j]){
                    dp[i] = Math.max(dp[i], dp[j]+1);
                }
            }
        }
        int res = 0;
        for(int i = 0; i < dp.length;i++){
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

LeetCode 354. 俄罗斯套娃信封问题

在这里插入图片描述

解题思路

这道题目其实是最长递增子序列的一个变种，因为每次合法的嵌套是大的套小的，相当于在二维平面中找一个最长递增的子序列，其长度就是最多能嵌套的信封个数。
先对宽度w进行升序排序，如果遇到w相同的情况，则按照高度h降序排序；之后把所有的h作为一个数组，在这个数组上计算 LIS 的长度就是答案。

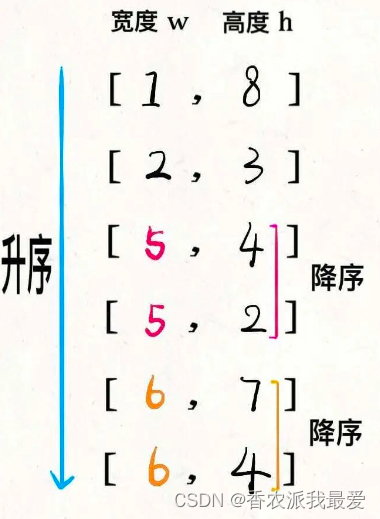
在这里插入图片描述
对宽度w从小到大排序，确保了w这个维度可以互相嵌套，所以我们只需要专注高度h这个维度能够互相嵌套即可。

其次，两个w相同的信封不能相互包含，所以对于宽度w相同的信封，对高度h进行降序排序，保证 LIS 中不存在多个w相同的信封。

代码实现

class Solution {
    public int maxEnvelopes(int[][] envelopes) {

        Arrays.sort(envelopes, new Comparator<int[]>(){
            public int compare(int[] a, int[] b){
                return a[0] == b[0]?b[1]-a[1]:a[0]-b[0];
            }
        });

        int[] nums = new int[envelopes.length];
        for(int i = 0;i < envelopes.length;i++){
            nums[i] = envelopes[i][1];
        }
        return lengthOfLIS(nums);
    }

    public int lengthOfLIS(int[] nums){
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);
        for(int i = 0;i < nums.length;i++){
            for(int j = 0;j < i;j++){
                if(nums[i]>nums[j]){
                    dp[i] = Math.max(dp[i], dp[j]+1);
                }
            }
        }
        int res = 0;
        for(int i = 0; i < nums.length;i++){
            res = Math.max(dp[i], res);
        }
        return res;
    }
}