目录
1.算法描述
2.matlab算法仿真效果
3.MATLAB核心程序
4.完整MATLAB
1.算法描述
人工势场法原理是:首先构建一个人工虚拟势场,该势场由两部分组成,一部分是目标点对移动机器人产生的引力场,方向由机器人指向目标点,另一部分是障碍物对移动机器人产生的斥力场,方向为由障碍物指向机器人。运行空间的总势场为斥力场和引力场共同叠加作用,从而通过引力和斥力的合力来控制移动机器人的移动。
物理学的势(potential),也称做“位”,是一种能量概念。在保守场里,把一个单位质点(如重力场中的单位质量,静电场中的单位正电荷)从场中的某一点A移到参考点,场力所作的功是一个定值。也就是说,在保守场中,单位质点在A点与参考点的势能之差是一定的,人们把这个势能差定义为保守场中A点的“势”。
人工势场法路径规划是由Khatib提出的一种虚拟力法(Oussama Khatib,Real-Time Obstacle Avoidance for Manipulators and Mobile Robots. Proc of The 1985 IEEE.)。它的基本思想是将机器人在周围环境中的运动,设计成一种抽象的人造引力场中的运动,目标点对移动机器人产生“引力”,障碍物对移动机器人产生“斥力”,最后通过求合力来控制移动机器人的运动。应用势场法规划出来的路径一般是比较平滑并且安全,但是这种方法存在局部最优点问题。
人工势场就像构建了一个吸铁石,包括引力场和斥力场。黑色为障碍物,箭头为智能体要运动的方向,目标点为“Goal”。智能体按照箭头的方向到达“Goal”,目标点像有着“吸引力”一样吸引着智能体靠近。而在障碍物附近,智能体逆着箭头的方向,好像对智能体产生“排斥力”。智能体前进的方向就是这两种力的合力的方向。


当然仅仅只有引力势场是不够的,我们还需要让机器人懂得避开地图中的障碍物,这时斥力势场便有用武之地了,斥力势场的会构建一个距离障碍物越近,斥力越大的特殊势场。 这个过程其实非常好理解,引力势场负责吸引机器人从起点朝着终点运动,斥力势场负责规避地图中的障碍。 通常我们会用下面这个函数来构建斥力势场:
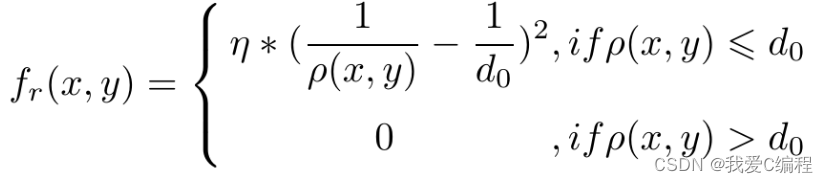
人工势场法路径规划是由Khatib提出的一种虚拟力法(Oussama Khatib,Real-Time Obstacle Avoidance for Manipulators and Mobile Robots. Proc of The 1985 IEEE.)。它的基本思想是将机器人在周围环境中的运动,设计成一种抽象的人造引力场中的运动,目标点对移动机器人产生“引力”,障碍物对移动机器人产生“斥力”,最后通过求合力来控制移动机器人的运动。应用势场法规划出来的路径一般是比较平滑并且安全,但是这种方法存在局部最优点问题。
人工势场法是一种经典的机器人路径规划算法。该算法将目标和障碍物分别看做对机器人有引力和斥力的物体,机器人沿引力与斥力的合力来进行运动。
(a) 当物体离目标点比较远时,引力将变的特别大,相对较小的斥力在甚至可以忽略的情况下,物体路径上可能会碰到障碍物
(b)当目标点附近有障碍物时,斥力将非常大,引力相对较小,物体很难到达目标点
(c)在某个点,引力和斥力刚好大小相等,方向想反,则物体容易陷入局部最优解或震荡
人工势场法(Artificial Potential Field)简称 APF,属于局部路径规划中常使用的一种方法。将传统力学中“场”的概念引入该方法,假设让智能体在这种虚拟力场下进行运动。如何设计引力场影响着该算法的性能,同时存在容易陷入局部极小点的局限性。
2.matlab算法仿真效果
matlab2017b仿真结果如下:
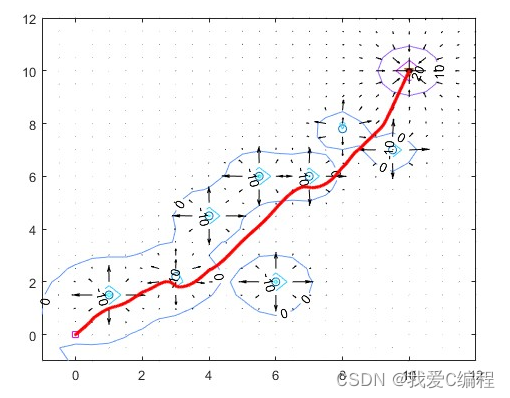
3.MATLAB核心程序
%
Xo=[0 0];%
k=20;%
K=0;%
m=5;%
Po=2;%0
n=8;%
a=0.5;
l=0.05;%
J=500;%
%Po
%end
%
Xsum=[10 10;1 1.5;3 2.2;4 4.5;7 6;6 2;5.5 6;8 7.8;9.5 7];%(n+1)*2[10 10]
Xj=Xo;%j=1Xj
[x,y]=meshgrid(-1:0.5:12,-1:0.5:12);
z=0.5*k./(sqrt((x-10).^2+(y-10).^2+0.09))-0.5*m*(1./(sqrt((x-1).^2+(y-1.5).^2+0.09))-1/3.5).^2-0.5*m*(1./(sqrt((x-3).^2+(y-2.2).^2+0.09))-1/3.5).^2 ...
-0.5*m*(1./(sqrt((x-4).^2+(y-4.5).^2+0.09))-1/3).^2-0.5*m*(1./(sqrt((x-7).^2+(y-6).^2+0.09))-1/3).^2-0.5*m*(1./(sqrt((x-6).^2+(y-2).^2+0.09))-1/3.5).^2 ...
-0.5*m*(1./(sqrt((x-5.5).^2+(y-6).^2+0.09))-1/4).^2-0.5*m*(1./(sqrt((x-8).^2+(y-7.8).^2+0.09))-1/3).^2-0.5*m*(1./(sqrt((x-9.5).^2+(y-7).^2+0.09))-1/3).^2;
% contour(x,y,z,[-50:20:1000]);
[C,h]=contour(x,y,z,[-80:10:300]);
set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)
colormap cool
[px,py]=gradient(z);%x,y
quiver(x,y,px,py,'k') %
p=sqrt(px.^2+py.^2);
%%
t=1;
M(t)=getframe;
t=t+1;
%*********************************
for j=1:J%
Goal(j,1)=Xj(1);%Goal
Goal(j,2)=Xj(2);
%
Theta=compute_angle(Xj,Xsum,n);%ThetaX
%
Angle=Theta(1);%Theta1
angle_at=Theta(1);%angle_at
[Fatx,Faty]=compute_Attract(Xj,Xsum,k,Angle,0,Po,n);%x,y
for i=1:n
angle_re(i)=Theta(i+1);%nn
end
%
[Frerxx,Freryy,Fataxx,Fatayy]=compute_repulsion(Xj,Xsum,m,angle_at,angle_re,n,Po,a);%x,y
%j
Fsumyj=Faty+Freryy+Fatayy;%y
Fsumxj=Fatx+Frerxx+Fataxx;%x
Position_angle(j)=atan(Fsumyj/Fsumxj);%x
%
Xnext(1)=Xj(1)+l*cos(Position_angle(j));
Xnext(2)=Xj(2)+l*sin(Position_angle(j));
%
Xj=Xnext;
X=Goal(:,1);
Y=Goal(:,2);
plot(X,Y,'.r');
M(t)=getframe;t=t+1;
%
if ((Xj(1)-Xsum(1,1))>0)&((Xj(2)-Xsum(1,2))>0)%
K=j;%
break;
%j
end%if
end%
A794.完整MATLAB
V





![使用[阿里问题定位神器]Arthas入门](https://img-blog.csdnimg.cn/img_convert/becf2d23ceb129eb2635d714998be106.png)