目录
- ServerBootstrap.bind()
- initAndRegister()
- init()
- register()
- doBind0()
ServerBootstrap.bind()
在第一篇的HelloWorld中通过ServerBootstrap.bind()方法绑定端口号并最终启动Netty的服务,服务端的bind过程如下:
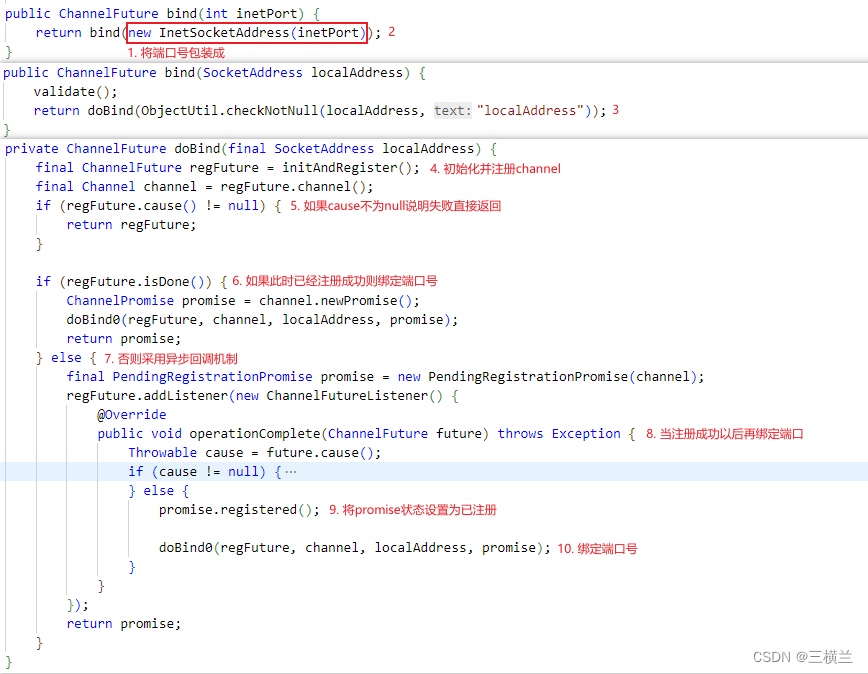
上面的代码主要分成两部分,第一部分是初始化与注册,第二部分为channel绑定端口号,一般来说会采用异步回调的机制。接下来我们具体分析这两部分的源码。
initAndRegister()
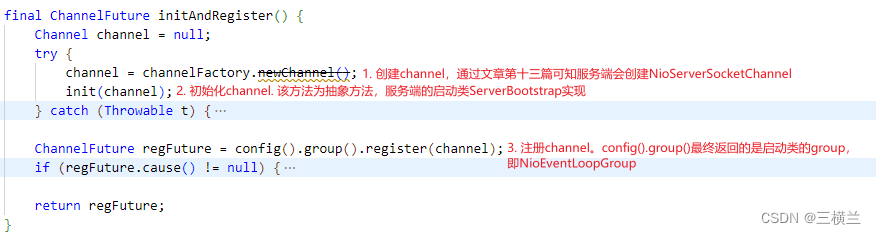
第一步创建channel的过程前面的文章已经分析过,第二步的init()为抽象方法,服务端会在ServerBootstrap中实现,第三步的注册过程会在NioEventLoopGroup中实现。
init()
初始化的过程主要是把在HelloWorld中设置的属性值填充,然后向pipeline中添加初始化handler,当channel注册成功后执行一些初始化的工作。
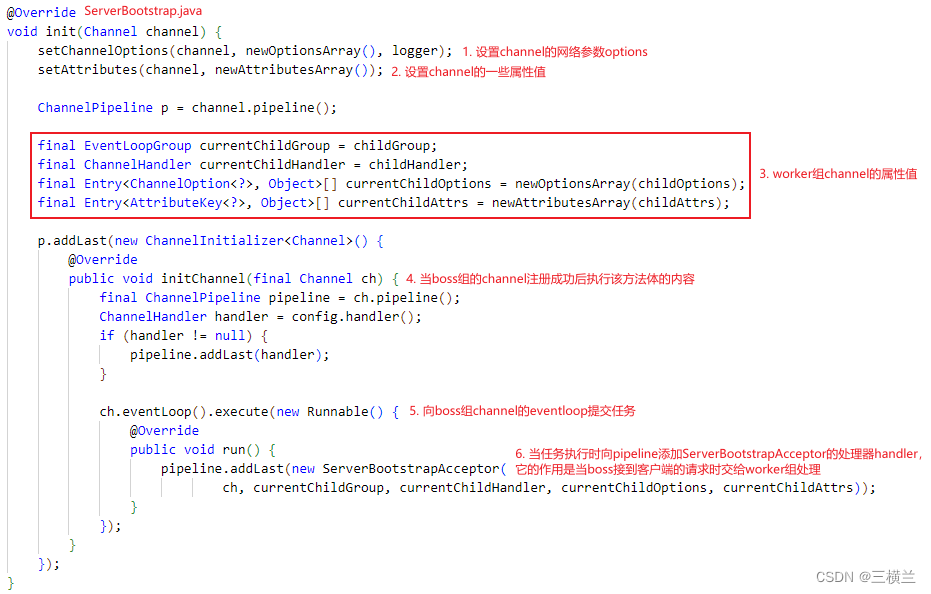
register()
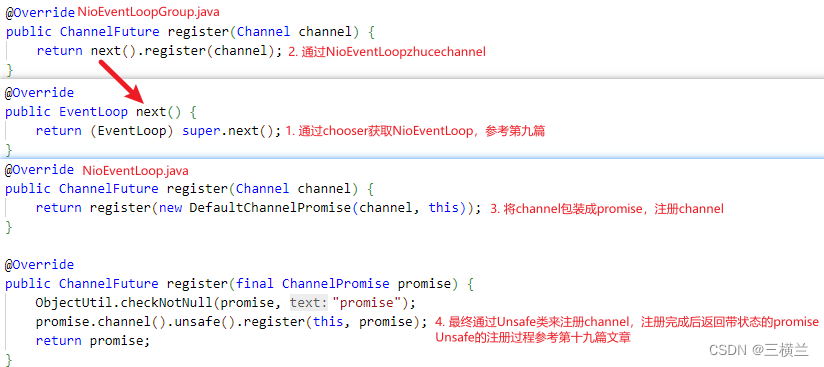
注册成功后会执行init()方法中向pipeline添加的ChannelInitializer的initChannel方法,即向NioEventLopp提交一个任务,该任务是向pipeline添加ServerBootstrapAcceptor。
doBind0()
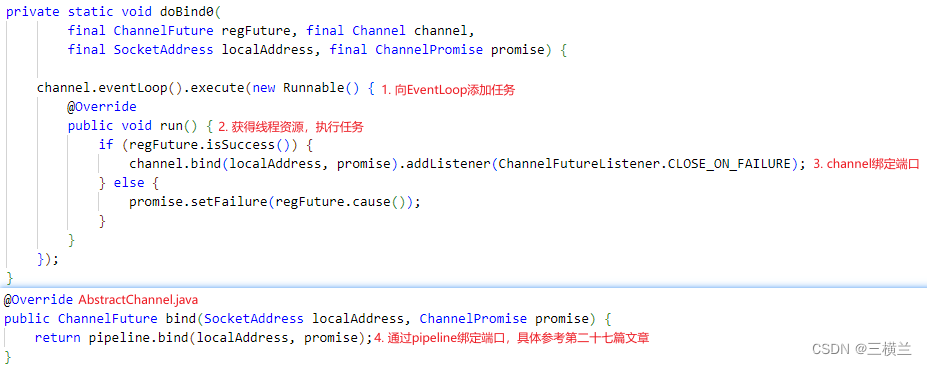
通过ServerBootstrap的bind()方法可知Netty很多工作都是异步执行的,在分析的时候需要多打断点或者log的形式分析,最后总结一下整个bind()的过程。
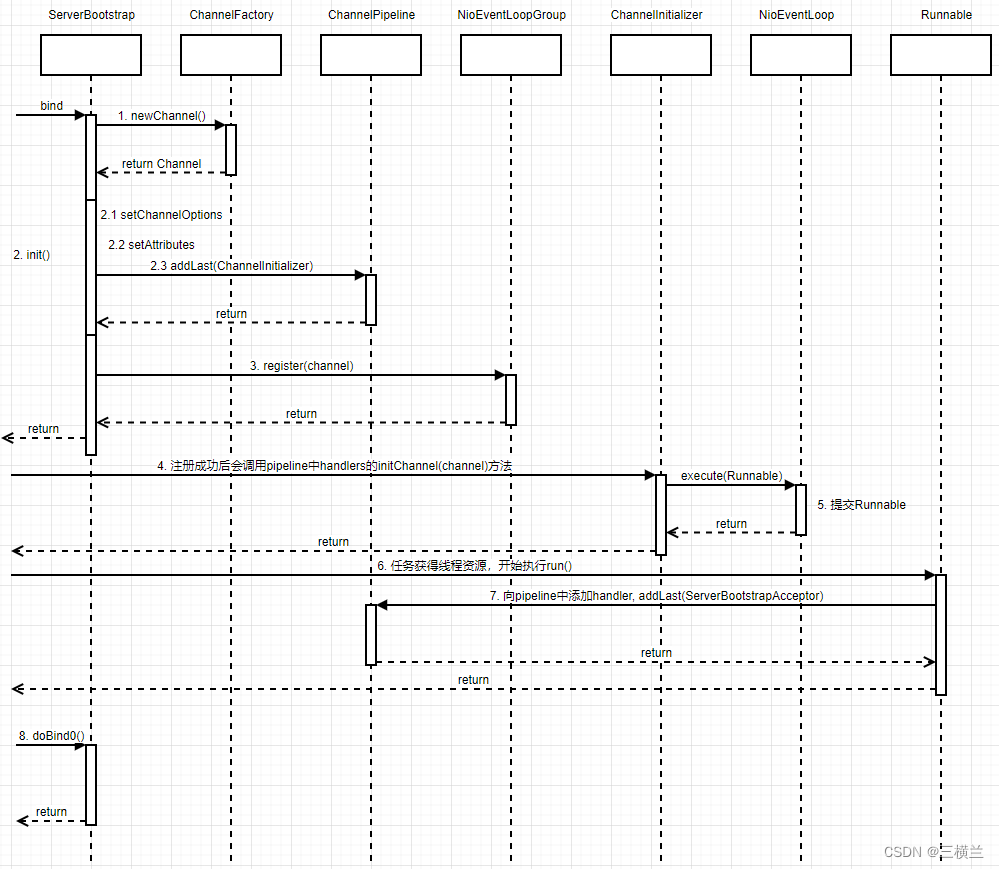
至此,**ServerBootstrap.bind()**的分析到此结束,感谢阅读。



![[Linux] 动态 / 静态库的生成与使用](https://img-blog.csdnimg.cn/59a5f24d2c13419fa62422456f5b64b3.png)