一、选择排序

思想：每趟在待排序元素中选取关键字最小的元素加入有序子列

不稳定性

空间复杂度：O(1)

时间复杂度：

void swap(int &a,int &b){
    int temp=a;
    a=b;
    b=temp;
}
void SelectSort(int A[],int n){
    for(int i=0;i<n-1;i++){                //一共进行n-1趟
        int min=i;                         //记录最小元素位置
        for(int j=i+1;j<n;j++)             //在[i...n-1]中选择最小的元素
            if(A[j]<A[min])    mig=j;      //更新最小元素值
        if(min=!=j)    swap(A[i],A[min]);  //封装的swap()函数，交换2个值
    }
}

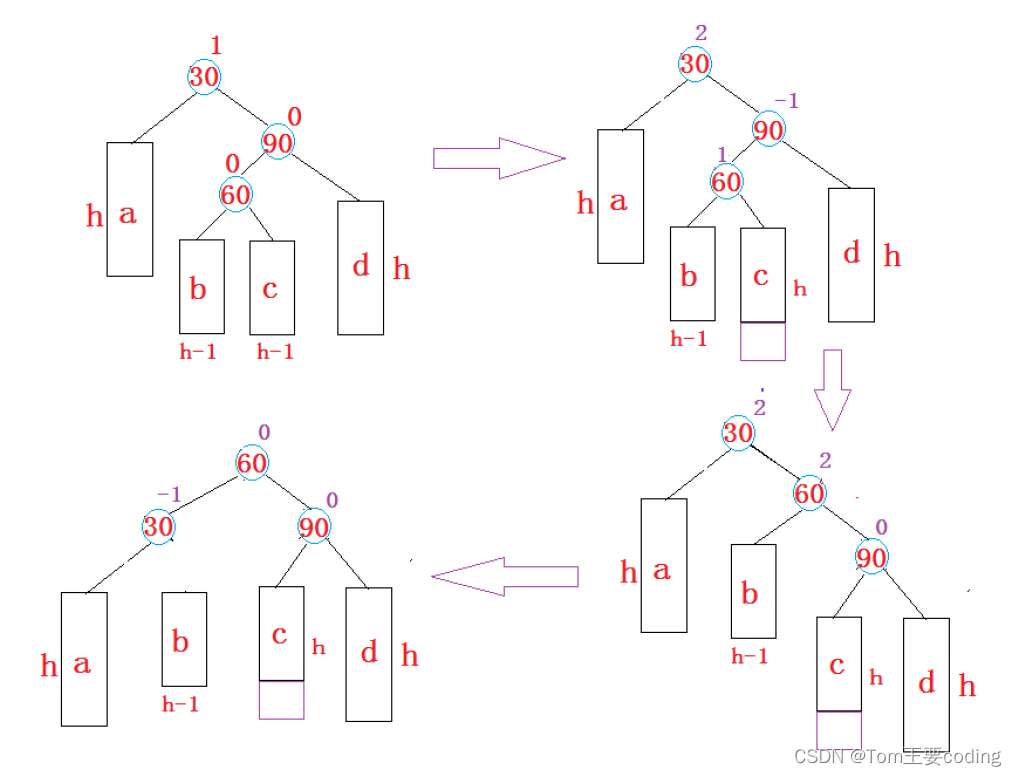
二、堆排序

二叉树的顺序存储，大根堆->{根>左右}，小根堆->{根<左右}

//建立大根堆
void BuildMaxHeap(int A[],int len){
    for(int i=len/2;i>0;i++)                //从后往前调整所有非终端叶结点
        HeadAdjust(A,i,len);
}
//已k为根的子树调整为大根堆
void HeadAdjust(int A[],int k,int    len){
    A[0]=A[k];                              //A[0]暂存子树的根结点
    for(int i=2*k;i<=len;i*=2){             //沿key较大的子结点向下筛选
        if(i<len&&A[i]<A[i+1])
            i++;                            //取key较大的子结点的下标
        if(A[0]>=A[i])                      //筛选结束
            break;
        else{
            A[k]=A[i];                      //将A[i]调整到双亲结点上
            k=i;                            //修改k值，以便继续向下筛选
        }
    }
    A[k]=A[0];                              //被筛选结点的值放入最终位置
}

排序

获取根第一个，又删除根后恢复大堆根，又取根，一直循环取完为止

//堆排序完成逻辑
void HeapSort(int A[],int len){
    BuildMaxHeap(A,len);        //初建大根堆
    for(int i=len;i>1;i--){     //n-1趟的交换和建堆过程
        swap(A[i],A[1]);        //堆顶元素和堆底元素交换
        HeapAdjust(A,1,i-1)     //把剩余的待排序元素整理成堆
    }
}

效率分析

关键字对比不超过4n，建堆时间O(n),排序时间

时间复杂度：

不稳定性

空间复杂度：O(1)

时间复杂度：

三、归并排序

思想：把两个或多个已经有序的序列合并成一个

2个数组值小的放入下方数组，小的和下面数组都后移一位

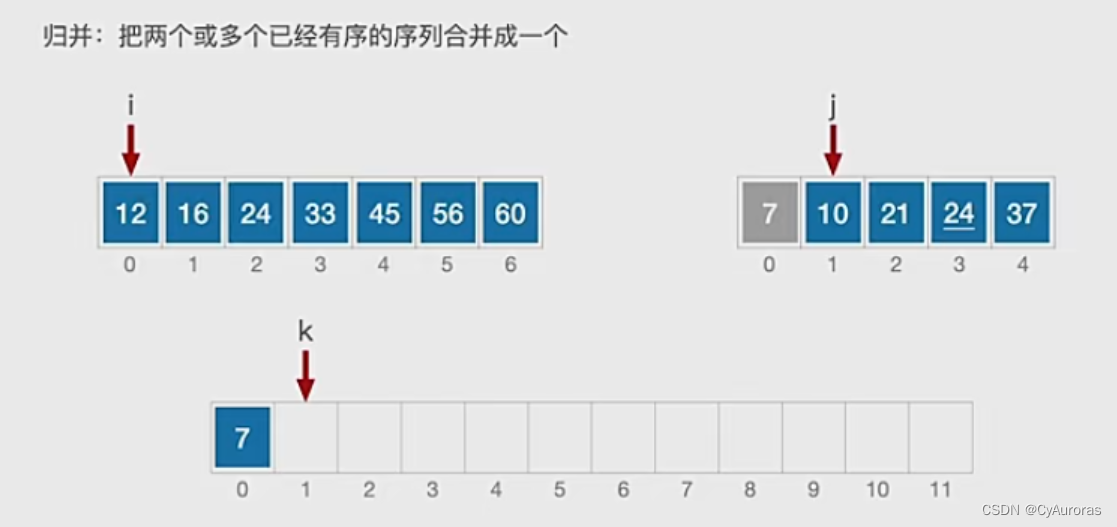
二路归并：两个有序序列合二为一最少对比2-1次

四路归并：四个有序序列合二为一最少对比 4-1次

m路归并：m个有序序列合二为一最少对比 m-1次

排序

int *B=(int *)malloc(n*sizeof(int));

//A[low...mid]和A[mid+1...high]各自有序，将两个部分归并
void Merge(int A[],int low,int mid,int high){
    int i,j,k;
    for(k=low;k<=high;k++)
        B[k]=A[k];                            //将A中所有元素复制到B
    for(i=low,j=mid+1,k=i;i<=mid&&j<=high;k++){
        if(B[i]<=B[j])
            A[k]=B[i++];                      //将较小值复制到A
        else
            A[k]=B[j++];
    }
    while(i<=mid)    A[k++]=B[i++];
    while(j<=high)    A[k++]=B[j++];
}

void MergeSort(int A[],int low,int high){
    if(low<high){
        int mid=(low+high)/2;        //从中间划分
        MergeSort(A,low,mid);        //对左半部分归并排序
        MergeSort(A,mid+1,high);     //对右半部分归并排序
        Merge(A,low,mid,high);       //归并
    }
}

分析

保证稳定性

空间复杂度：

时间复杂度：

四、基数排序

数值有个位、十位、百位..等等，第一趟以个位开始进行分配到[0~9]的队列中，结束后收集起来

后面以十位进行分配收集，百位后收集.....

//基数排序的链式存储
typedef struct LinkNode{
    int data;
    struct LinkNode *next;
}LinkNode,*LinkList;
typedef struct{                //链式队列
    LinkNode *front,*rear;
}LinkQueue;

保证稳定性

空间复杂度：