目录
一、实验内容
二、完成情况
三、数据分析
1.问题描述
2.编程思路
3.程序代码
4.程序运行结果
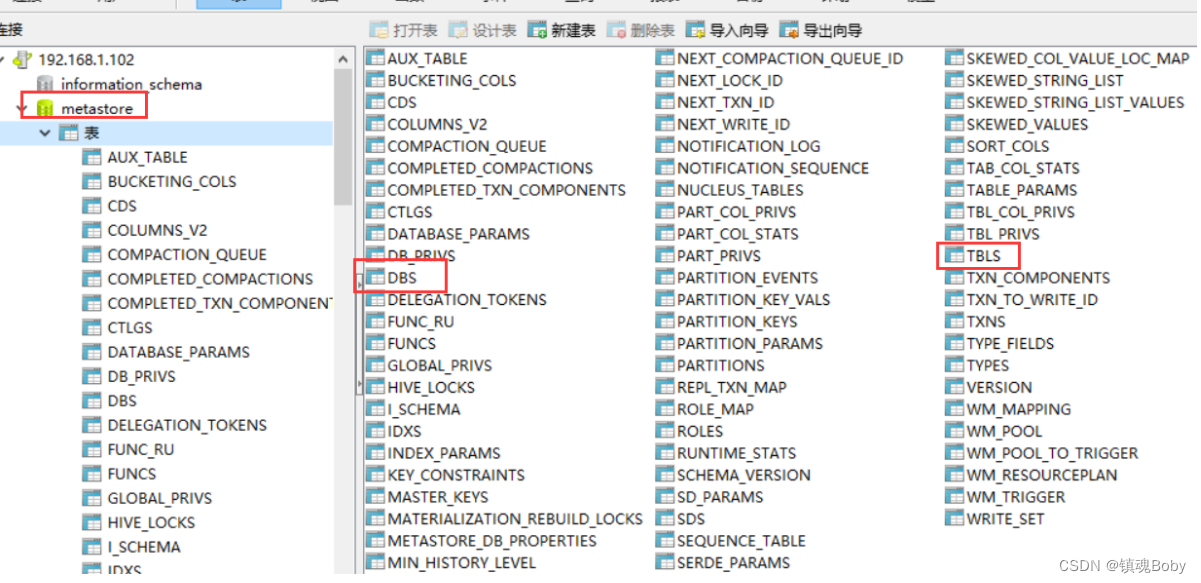
(1)2014年-2019年AQI时间序列折线图
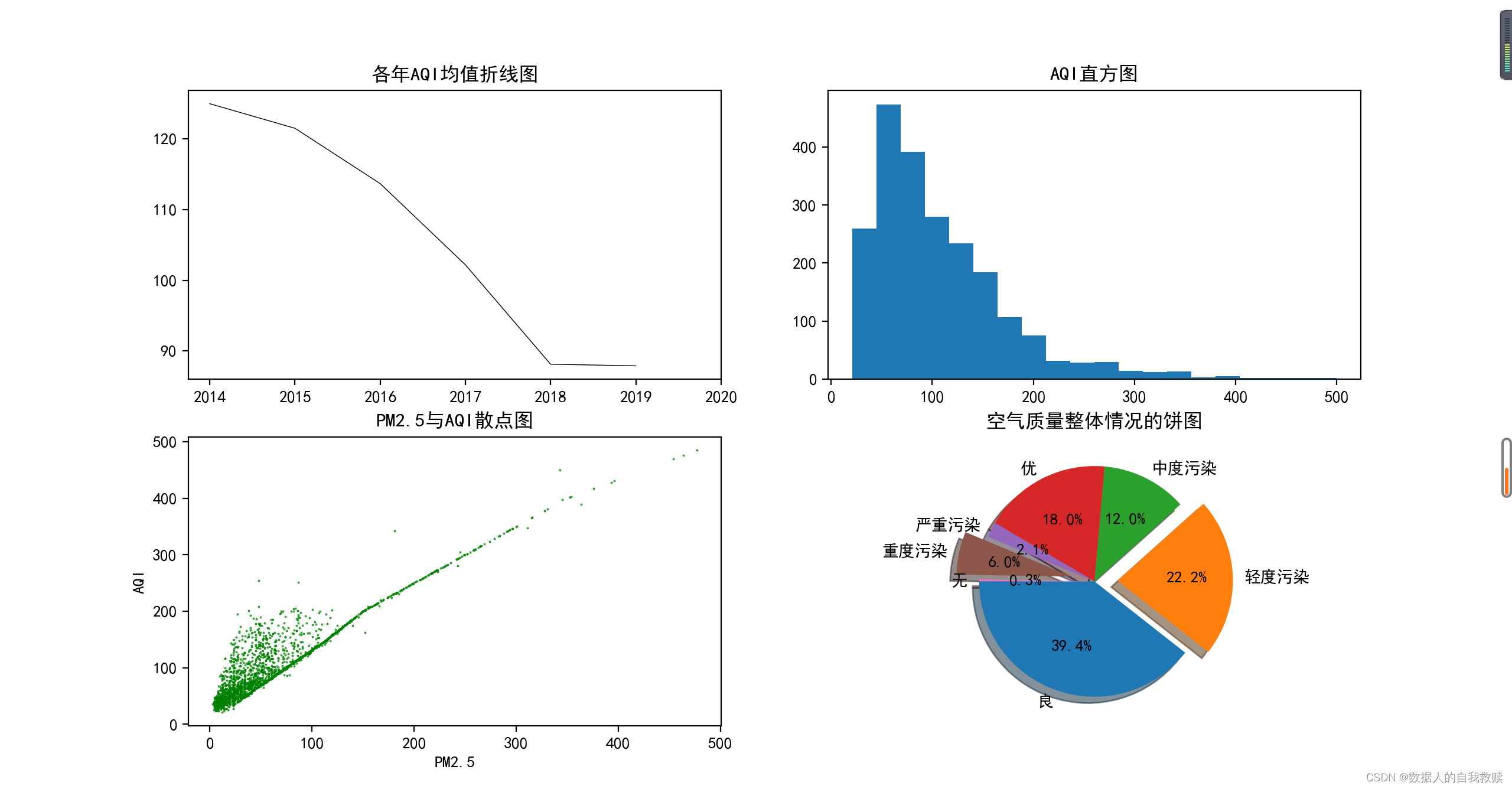
(2)各年AQI折线图、AQI直方图、PM2.5与AQI散点图、空气质量整体情况的饼图
(3)六种空气成分与AQI的散点图
5.结果分析
一、实验内容
对《北京市空气质量》数据进行数据分析。其中包括数据的导入、预处理、可视化。
二、完成情况
1.完成了《北京市空气质量的数据分析》
2.敲试了听课ppt上的代码,由于内容较多,放于实验报告最后的【附录】部分
三、数据分析
1.问题描述
根据《北京市空气质量》的excel数据对今年北京市空气质量进行分析
2.编程思路
(1)首先导入数据,利用pandas库进行导入
(2)其次进行数据预处理,主要针对异常值,找到后用NAN替代
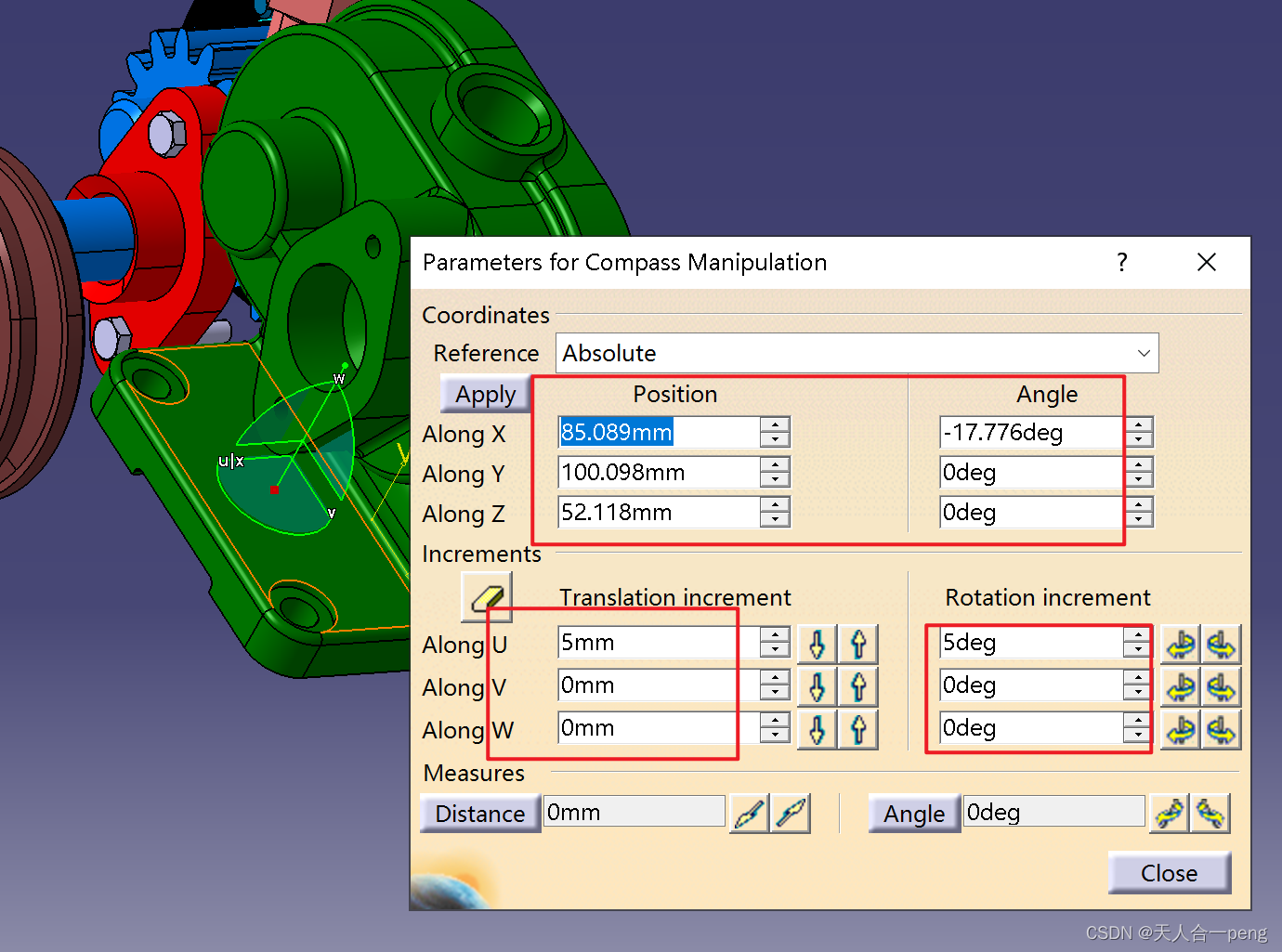
(3)绘制2014年-2019年AQI时间序列折线图,从空气质量指数的折线图直观地看2014年-2019年北京市空气质量的变化
(4)绘制各年AQI折线图,观看2014-2019年AQI均值的变动情况;绘制AQI直方图,看2014年-2019年AQI的分布;绘制PM2.5与AQI的散点图,分析PM2.5对AQI的影响;绘制质量等级的饼图,观看各个等级所占的比例
(5)在原有代码的基础上又编写了绘制六种空气成分与AQI的散点图,分析各个成分对AQI的影响
3.程序代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt#matplotlib的Pyplot子模块,指定别名为plt
#%matplotlib inline
#将matplotlib的图表直接嵌入到Notebook之中,或者使用指定的界面库显示图表,它有一个参数指定matplotlib图表的显示方式。inline表示将图表嵌入到Notebook中。
#Python提供了许多魔法命令,使得在IPython环境中的操作更加得心应手。魔法命令都以%或者%%开头,以%开头的成为行命令,%%开头的称为单元命令。行命令只对命令所在的行有效,而单元命令则必须出现在单元的第一行,对整个单元的代码进行处理。
#执行%magic可以查看关于各个命令的说明,而在命令之后添加?可以查看该命令的详细说明。
plt.rcParams['font.sans-serif']=['SimHei'] #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
data=pd.read_excel('D:\个人成长\学业\课程\python\实验\题目\北京市空气质量数据.xlsx') #要注意路径
#指定立即显式所绘图形,且通过参数设置解决图形中文显示乱码问题
data.isnull()
data=data.replace(0,np.NaN)
plt.figure(figsize=(10,5))
#利用函数plt.figure说明图形的一般特征,如这里指宽10高5
plt.plot(data['AQI'],color='black',linestyle='-',linewidth=0.5)
#利用函数plt.plot绘制序列折线图,同时指定折线颜色、线性、线宽等
plt.axhline(y=data['AQI'].mean(),color='red', linestyle='-',linewidth=0.5,label='AQI总平均值')
#在参数y指定位置上画一条平行于横坐标的直线,并给定直线图例文字
#plt.axvline在参数x指定位置上画一条平行于纵坐标的直线,并给定直线图例文字
data['年']=data['日期'].apply(lambda x:x.year)
AQI_mean=data['AQI'].groupby(data['年']).mean().values
#分组计算各年AQI的平均值
year=['2014年','2015年','2016年','2017年','2018年','2019年']
col=['red','blue','green','yellow','purple','brown']
for i in range(6):
plt.axhline(y=AQI_mean[i],color=col[i], linestyle='--',linewidth=0.5,label=year[i])
#利用for循环绘制多条平行于横坐标的直线,表征各年AQI平均值
plt.title('2014年至2019年AQI时间序列折线图')
plt.xlabel('年份')
plt.ylabel('AQI')
#指定图的标题,横纵坐标的坐标标签
plt.xlim(xmax=len(data), xmin=1)
plt.ylim(ymax=data['AQI'].max(),ymin=1)
#指定横纵坐标的取值范围
plt.yticks([data['AQI'].mean()],['AQI平均值'])
plt.xticks([1,365,365*2,365*3,365*4,365*5],['2014','2015','2016','2017','2018','2019'])
#在指定坐标刻度位置上给出刻度标签
plt.legend(loc='best')
#利用legend在指定位置(best表示最优位置)显式图例
plt.text(x=list(data['AQI']).index(data['AQI'].max()),y=data['AQI'].max()-20,s='空气质量最差日',color='red')
#利用text在指定的行列位置上显式指示文字
plt.show()
#表示此次绘图结束
import warnings
#导入warning模块,并指定忽略代码运行过程中的警告信息
warnings.filterwarnings(action = 'ignore')
plt.figure(figsize=(10,5))
plt.subplot(2,2,1)
#将绘图区域分成2行2列4个单元,且下一副图将在第2个单元显示
plt.plot(AQI_mean,color='black',linestyle='-',linewidth=0.5)
plt.title('各年AQI均值折线图')
plt.xticks([0,1,2,3,4,5,6],['2014','2015','2016','2017','2018','2019','2020'])
plt.subplot(2,2,2)
plt.hist(data['AQI'],bins=20)
#绘制AQI的直方图,图中包含20个柱形条,即将数据分成20组
plt.title('AQI直方图')
plt.subplot(2,2,3)
plt.scatter(data['PM2.5'],data['AQI'],s=0.5,c='green',marker='.')
#利用scatter绘制PM2.5和AQI的散点图,并指定点的大小、颜色和形状
plt.title('PM2.5与AQI散点图')
plt.xlabel('PM2.5')
plt.ylabel('AQI')
plt.subplot(2,2,4)
tmp=pd.value_counts(data['质量等级'],sort=False)
#等同:tmp=data['质量等级'].value_counts()
share=tmp/sum(tmp)
labels=tmp.index
explode = [0, 0.2, 0, 0, 0,0.2,0]
plt.pie(share, explode = explode,labels = labels, autopct = '%3.1f%%',startangle = 180, shadow = True)
#利用pie绘制饼图
plt.title('空气质量整体情况的饼图')
plt.show()
fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(10,5))
#说明绘图区域的宽和高,并指定将绘图区域分成2行2列4个单元。结果将赋值给fig和axes对象。
#可通过fig对整个图的特征进行设置,axes对应各个单元格对象
axes[0,0].plot(AQI_mean,color='black',linestyle='-',linewidth=0.5)
axes[0,0].set_title('各年AQI均值折线图')
axes[0,0].set_xticks([0,1,2,3,4,5,6])
axes[0,0].set_xticklabels(['2014','2015','2016','2017','2018','2019','2020'])
axes[0,1].hist(data['AQI'],bins=20)
axes[0,1].set_title('AQI直方图')
axes[1,0].scatter(data['PM2.5'],data['AQI'],s=0.5,c='green',marker='.')
axes[1,0].set_title('PM2.5与AQI散点图')
axes[1,0].set_xlabel('PM2.5')
axes[1,0].set_ylabel('AQI')
axes[1,1].pie(share, explode = explode,labels = labels, autopct = '%3.1f%%',startangle = 180, shadow = True)
axes[1,1].set_title('空气质量整体情况的饼图')
#通过图形单元索引的方式指定绘制单元,例如:axes[0,0]表示第1行第1列的单元格
#图标题、坐标轴标签、坐标轴刻度
fig.subplots_adjust(hspace=0.5)
fig.subplots_adjust(wspace=0.5)
#调节各图形单元行或列之间的距离
plt.show()
fig,axes=plt.subplots(nrows=2,ncols=3,figsize=(10,5))
#说明绘图区域的宽和高,并指定将绘图区域分成2行2列4个单元。结果将赋值给fig和axes对象。
#可通过fig对整个图的特征进行设置,axes对应各个单元格对象
axes[0,0].scatter(data['PM2.5'],data['AQI'],s=0.5,c='green',marker='.')
axes[0,0].set_title('PM2.5与AQI散点图')
axes[0,0].set_xlabel('PM2.5')
axes[0,0].set_ylabel('AQI')
axes[0,1].scatter(data['PM10'],data['AQI'],s=0.5,c='green',marker='.')
axes[0,1].set_title('PM10与AQI散点图')
axes[0,1].set_xlabel('PM10')
axes[0,1].set_ylabel('AQI')
axes[0,2].scatter(data['SO2'],data['AQI'],s=0.5,c='green',marker='.')
axes[0,2].set_title('SO2与AQI散点图')
axes[0,2].set_xlabel('SO2')
axes[0,2].set_ylabel('AQI')
axes[1,0].scatter(data['CO'],data['AQI'],s=0.5,c='green',marker='.')
axes[1,0].set_title('CO与AQI散点图')
axes[1,0].set_xlabel('CO')
axes[1,0].set_ylabel('AQI')
axes[1,1].scatter(data['NO2'],data['AQI'],s=0.5,c='green',marker='.')
axes[1,1].set_title('NO2与AQI散点图')
axes[1,1].set_xlabel('NO2')
axes[1,1].set_ylabel('AQI')
axes[1,2].scatter(data['O3'],data['AQI'],s=0.5,c='green',marker='.')
axes[1,2].set_title('O3与AQI散点图')
axes[1,2].set_xlabel('O3')
axes[1,2].set_ylabel('AQI')
#通过图形单元索引的方式指定绘制单元,例如:axes[0,0]表示第1行第1列的单元格
#图标题、坐标轴标签、坐标轴刻度
fig.subplots_adjust(hspace=0.5)
fig.subplots_adjust(wspace=0.5)
#调节各图形单元行或列之间的距离
plt.show()4.程序运行结果
(1)2014年-2019年AQI时间序列折线图

(2)各年AQI折线图、AQI直方图、PM2.5与AQI散点图、空气质量整体情况的饼图
 (3)六种空气成分与AQI的散点图
(3)六种空气成分与AQI的散点图
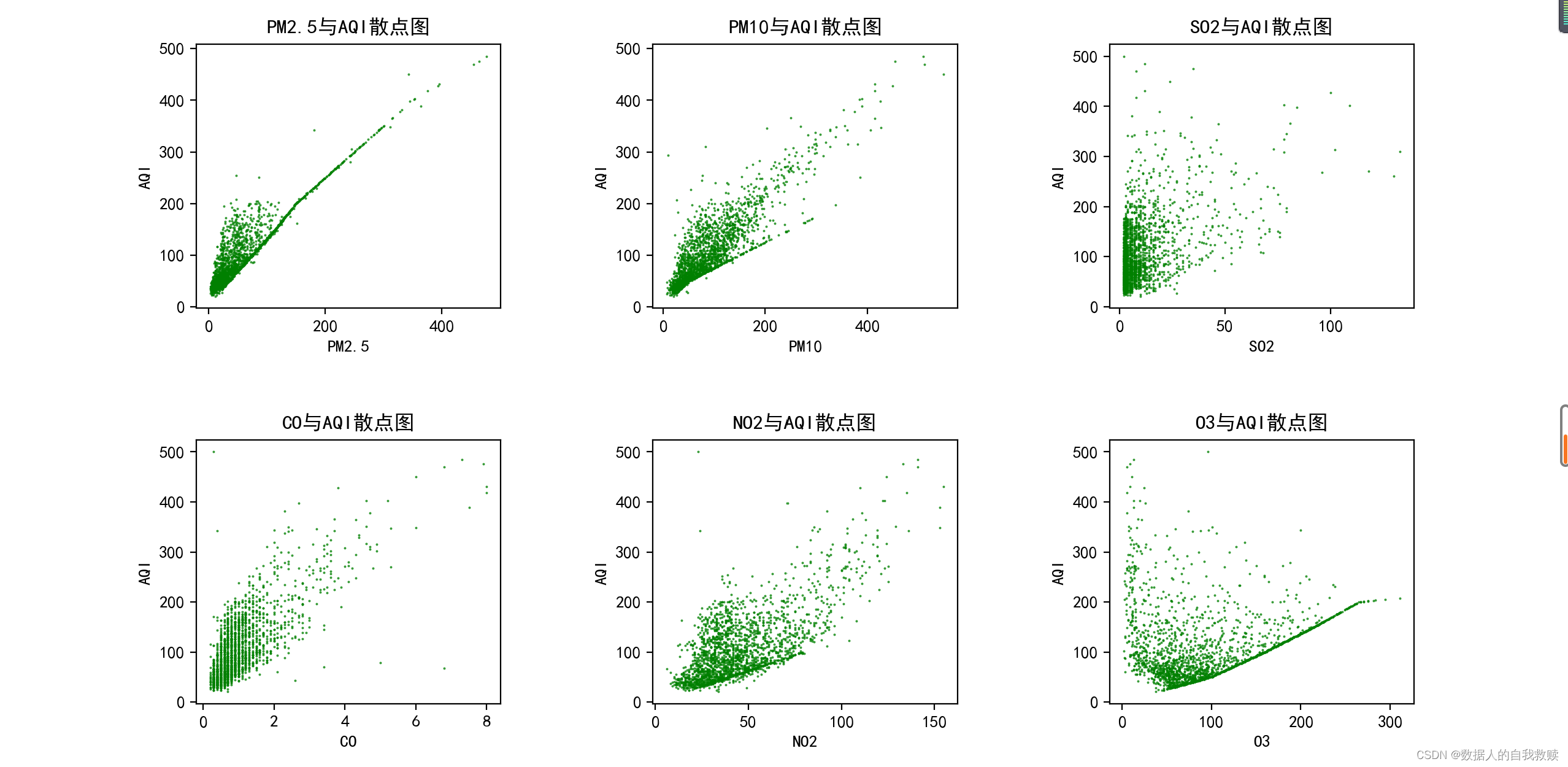
5.结果分析
从2014年-2019时间折线图可知,AQI有周期性变动,但总体上看AQI逐年降低,即北京市空气质量在逐年改善,这从各年AQI均值折现也可以看出;从直方图可以看出,AQI集中在60~70附近,即良附近,即近年北京市空气质量大多为良,这一点从空气质量等级的饼图可以得到验证;从AQI与空气成分的散点图可以看出,AQI与PM2.5、PM10、CO有较强的正相关关系,另外三个成分相关关系弱一些。
综上所述,北京市空气质量在逐年改善,但仍需进一步努力;多植树造林,增加绿化面积对改善空气成分有帮助,进而可以改善空气质量。