系列分享：

OCPC系列 - OCPC介绍扫盲贴来啦_高阳很捷迅的博客-CSDN博客

OCPC系列 - PID算法（理解PID算法）-比例控制算法、积分控制算法、微分控制算法_高阳很捷迅的博客-CSDN博客

---

名词解释

先简单介绍下以下名称解释，方便下面阅读。

名称	含义	备注
ecpm(effective cost per mille)	预估千次展现收益
ectr (effective Click-Through-Rate)	预估点击率
ecvr （effective conversion Rate）	预估转化率
given_CPA ( given Cost Per Action)	cpa价格	广告主cpa出价
real_CPA (real Cost Per Action)	cpa实际价格	代表实际投放出来的转化成本，他等于花费除以转化个数
Bidcpc ( bid cpc)	cpc出价
OCPC（Optimized Cost Per Click）	以目标转化为优化方式的点击出价

1. 业务介绍

广告行业的排序，基本都是依据ecpm排序

ecpm（预估千次收益）=

eCTR（预估点击率）*eCVR（预估转化率）*CPA（转化成本）* k (调控因子) * 1000

1.1 广告行业的广告投放流程

召回：

在一定的时间与资源限制下，从所有可能的候选集中选出一个合适大小的候选子集，实现某种指标的最大化

主要解决两个子问题：

• • 子问题1：广告与当前流量匹配；
  • 子问题2：广告处于可投放的状态。

排序：

对所有召回的内容进行打分排序，选出得分最高的几个结果推荐给用户，目前评分均是以ecpm打分.

常规模型（离线模型）：离线训练好模型,对所有用户做预测,将预测结果存起来

实时模型： 在线用户请求的时候，根据用户上下文数据，实时预估，返回给对应用户

因为粗排是可选的，对于大多数推荐系统来说，通常在线部分的主体分为两个阶段就够，第一个阶段是召回，第二个阶段是排序。当然还有说竞价，竞价其实是包含在排序中，我们可以举例说明下：

如: 广告主A和B设置的目标CPA均为100元；在OCPC二阶段模式下，系统计算出某广告位A和B的预估点击率eCTR_A、eCTR_B分别为0.1、0.2,预估转化率eCVR_A、eCVR_B分别为0.1、0.3，那么系统计算出的A和B的排序水平分别为：

Rank_A = eCTR_A*eCVR_A*100 = 1

Rank_B = eCTR_B*eCVR_B*100 = 6

此时，B胜出，且系统将此次广告的价格实时调整为：

CPC_A = eCVR_A*100 = 1

CPC_B = eCVR_B*100 = 3

real_cpa = CPC_B/eCVRB = 90 real_cpa价格。

第一阶段：cpc正常跑，第二阶段：看ctr, cvr , 调价因子：k , cvr

oCPM的竞价依据=广告系统的实时出价=平台预估eCPM=bid_CPA（广告主设置的转化出价）*eCVR（从点击到转化的比例预估）*eCTR（点击率预估）*智能调控因子。

2 算法角度解决ocpc问题

一是要给出ctr, cvr的预估模型，二是要保证cpa的误差率；

特征工程

特征主要有用户画像（user profile）、用户行为（user behavior）、广告（ad）和上下文（context）四部分组成

常用的特征值收集：用户（性别、年龄、地域、分否、教育、消费能力、公司行业、手机号、手机颜色、手机电池、手机生命周期）、广告（ID、主ID、APPID、app类目、创意目录）、上下文（广告位ID、网络类型、IP地址、版本）、时间（1天4个阶段、周末、工作日、节假日、第几周、年第几周）、统计（广告1、3、7、30的CTR、用户1、3、7、30的CTR）、交叉（广告和用户的交叉，比如年龄、性别、城市和广告维度的交叉）

召回算法

传统协同召回算法

• 基于协同过滤的召回算法
• 基于矩阵分解的召回算法

示例:

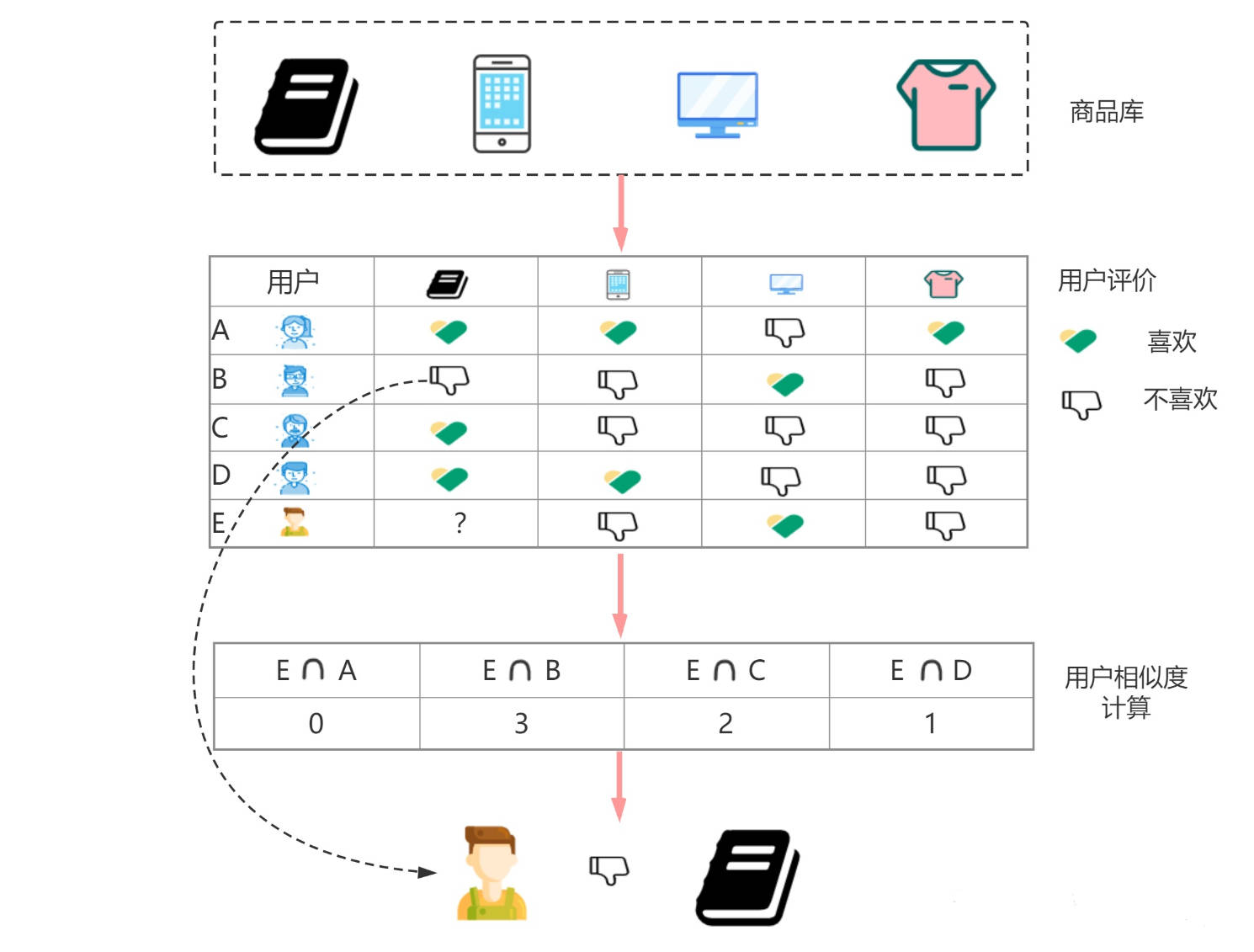
广告与当前用户匹配度

机器学习召回算法

1. LR，CNN+RNN ， LR逻辑回归算法，可解释性强， cnn, rnn需要更多的样本，解释性差些，但更智能
2. Embedding
3. EGES——阿里巴巴Graph Embedding方法
4. DSSM——经典的双塔召回模型

ctr, cvr的预估模型需要算法

点击率 (CTR) 和转化率 (CVR) 预测是一个至关重要的构建框直接决定后续出价策略以推动 RTB 广告计划效果

CTR

1. FM算法 ，FFM等（因子分解机，Factorisation machine）
2. 决策树算法 （简单的非线性监督学习方法）
3. DNN/DEEPFM 等等
4. lookalike算法

CVR

问题：数据量少，数据稀疏

1. 阿里CVR预估模型之ESMM， ESM2（ESMM优化版，解决数据稀疏）
2. DBMTL
3. GMSL

cpa的误差率

CPA误差，t0,t1,t2不同时段的

（1）cpa_delta（差值） = given_cpa - real_cpa

（2）cpa_ratio（误差比） = given_cpa / real_cpa

（3）cpa_ratio_delta（误差率增量） = given_cpa / real_cpa - 1

保证cpa的误差率，我们可以用到的算法：

1. PID算法

PID即：Proportional（比例）、Integral（积分）、Differential（微分）的缩写。顾名思义，PID控制算法是结合比例、积分和微分三种环节于一体的控制算法，它是连续系统中技术最为成熟、应用最为广泛的一种控制算法。

举例：

• 真实CPA>120%*CPA出价：赔钱，计费比过高
• 真实CPA<100%*CPA出价：亏钱，计费比小于1

pid因子就是用来控制ecpm出价，防止赔钱，也防止亏钱（基于目前的真实CPA差距）

• 赔钱：pid小于1，低估转化，保证广告主稳拿转化，降成本
• 亏钱：pid大于1，高估转化，保证广告被充分点击，提收入
• ecpm = ctr*cvr*cpa出价*1000*pid

1. 保序回归校准法（facebook）

给定了一个无序的数字序列，通过修改每个元素的值，得到一个非递减的数字序列，要求是使得误差（预测值和实际值差的平方）最小。比如在动物身上实验某种药物，使用了不同的剂量，按理说剂量越大，有效的比例就应该越高，但是如果发现了剂量大反而有效率降低了，这个时候就只有把无序的两个元素合并了，重新计算有效率，直到计算出来的有效率不大于比下一个元素的有效率