---

前言

其实机器学习也好，深度学习也罢，在我看来，代码编程终究是不重要的，因为现成的库，其数学原理，其公式推导才是我们需要理解的地方

一、NFL是什么？

没有免费的午餐定理，名字很有意思，因为它说明的是，对于用来解决某个问题的模型，或者预测模型，分类模型，它们其实在真实预测函数概率一样的时候，每一个模型其实是没有优劣的。我们要做的就是重复结合实际，不要空想，不同的有不同的情况

二、表现形式

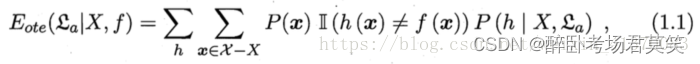
三、介绍

• 第一个Eote 值得是外训练误差，其中o是outer ，其中t是training，其中e是error
• 外训练误差指的一个训练好的模型，在外部也就是没有训练过的样本的预测结果的误差
• 其中X是训练的样本
• _x_是总共的样本空间
• f是真实的函数
• h是预测函数，是训练出来的模型
• 中间的||是逻辑符号，即表示预测值与真实值是否相等，相等则是为0，不相等为1。也就是看是不是有误差

四、手动推导

• 首先假设对于所有的真实函数f来说，概率是相等的，当然不可能是相等的，这里我们假设
  
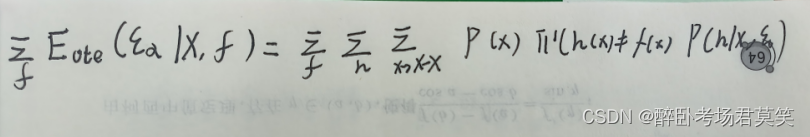
• 然后我们将求和放到只有他们变量的式子里面，f只有逻辑表达有，h只有第二个概率表达有，x只有第一个概率表达有，于是可以得到：

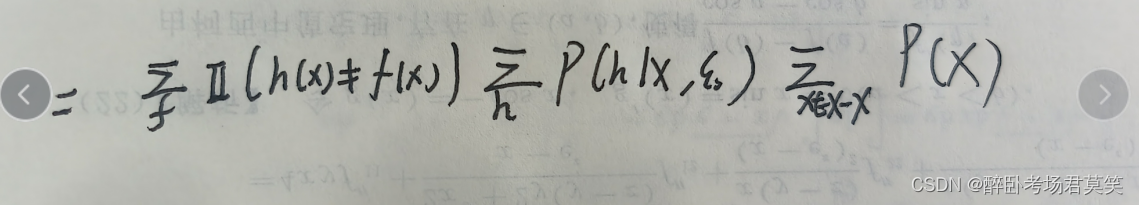
• 其中第一个概率肯定是唯一的，因为它求和了所有可能，就好像你抛一枚硬币，求它是正面或者是反面的概率一样，你把正面的概率加上反面的概率一定是1
  
• 然后我们看第一个逻辑表达式，其实呀，逻辑说的不就是预测值是不是等于真实值吗？我们可以假设x有两个样本x0和x1，那么要么相等，要么不相等，总共就四种情况，看我给出的下图：
  
• 那么好了其实对于一个样本来说，他的真实值只会是确定的，就好比，明天下雨活不下雨，你预测下雨，但是对于明天来说，下不下雨到了那天必定是确定的。你这几种情况，不管最终x0是预测0也好，1也罢。x1也一样，终究只会站一半，也就是一半的概率。所有概率就是1/2
• 但是这里是概率就和，也就是f的个数是多少，那就是2^|x|个了，你想每一个两种选择，总共|x|个。
• 于是得到最终结果：

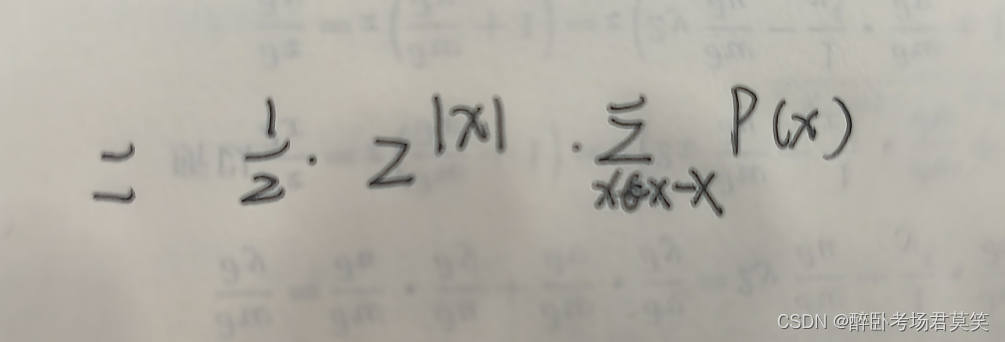
• 可以看到与f 与h都无关，当然前提f的概率相等，这在现实生活中是不可能存在的，但是我们要从中获得启示，模型其实在一开始的时候，都是差不多的，我们要结合实际，才能选出好模型