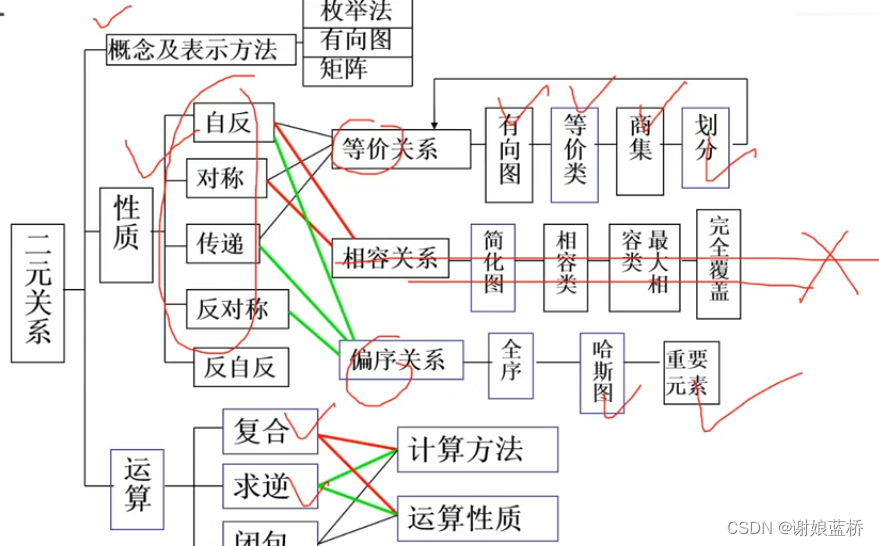
二元关系导图

等价关系 偏序关系 性质 运算 等价关系 重点

集合

常用集合符号

集合表示方法

不常考

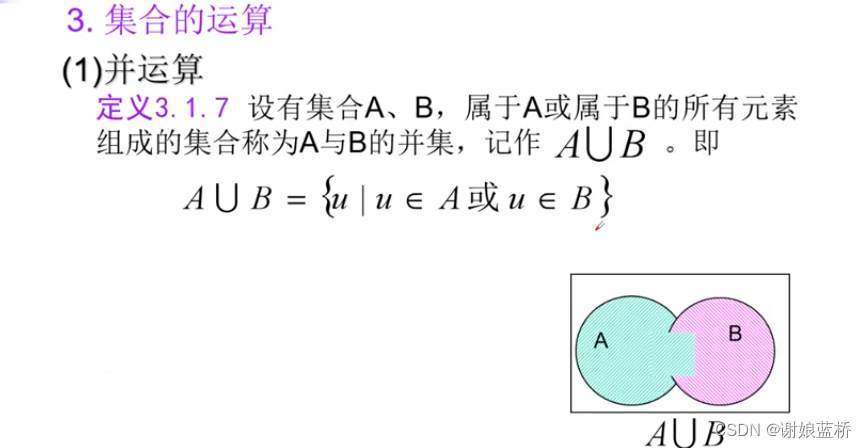
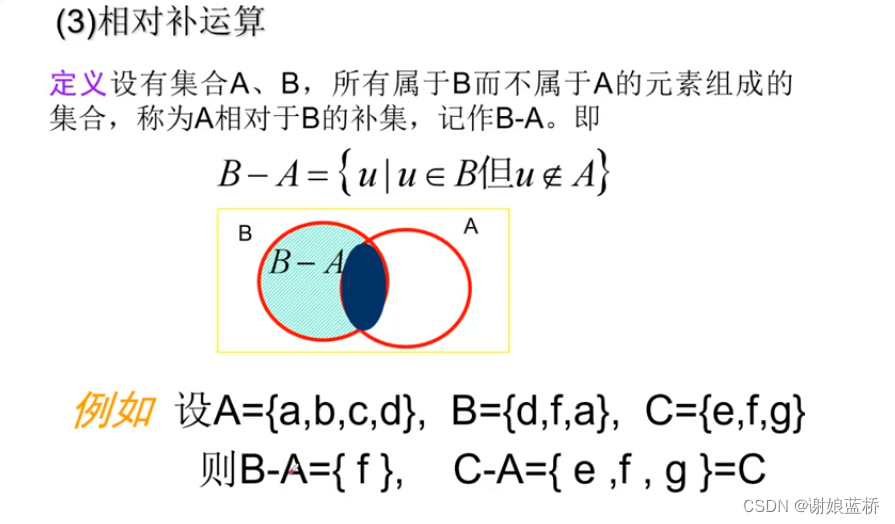
对等差等于两个集合的相对补的或关系

关系

序偶与笛卡尔积

笛卡尔积 ------不满足交换律 不满足结合律

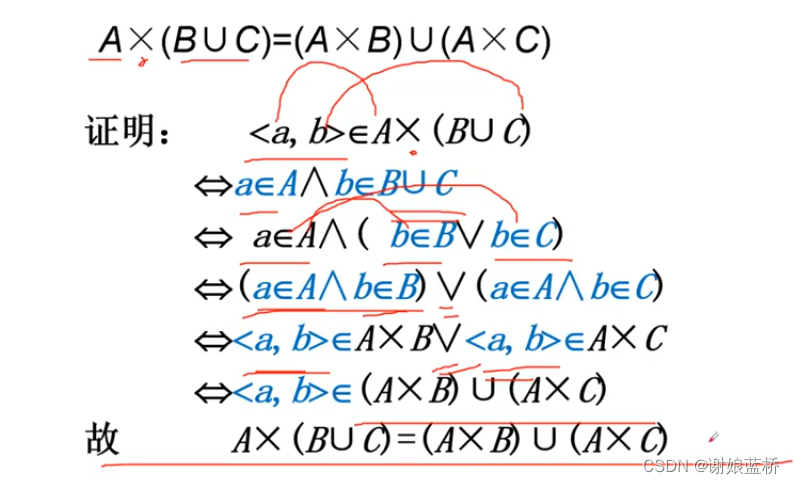
关系条件

1. 集合非空 且它的元素都是有序对
2. 集合是空集，空集也可看作关系
   

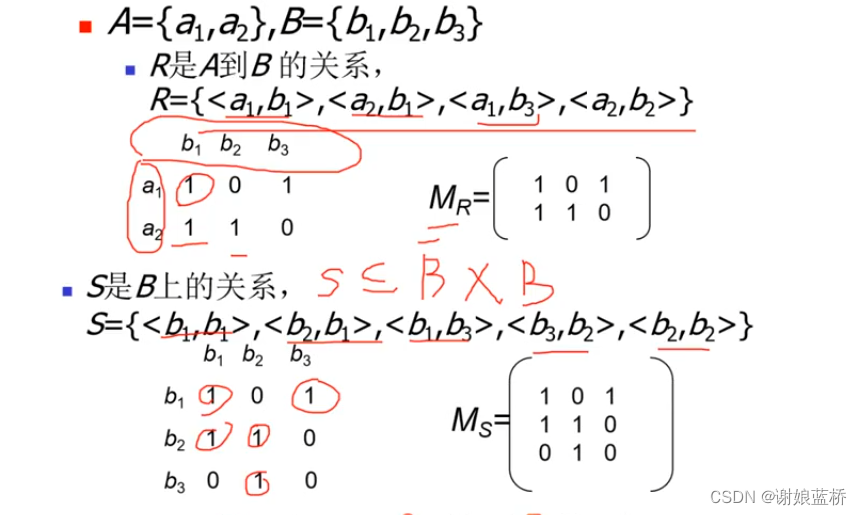
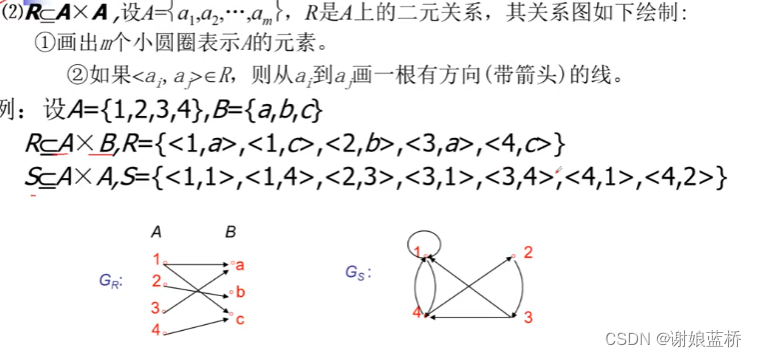
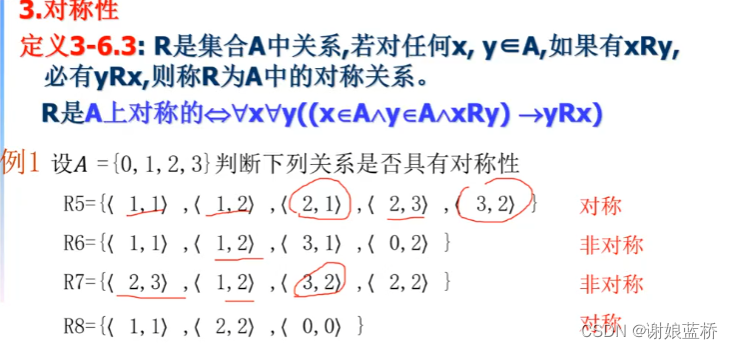
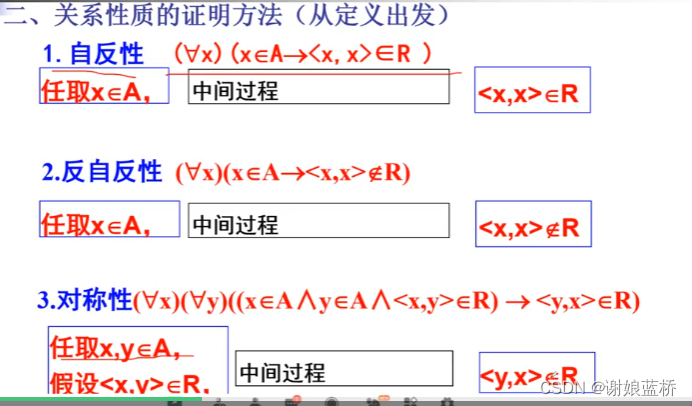
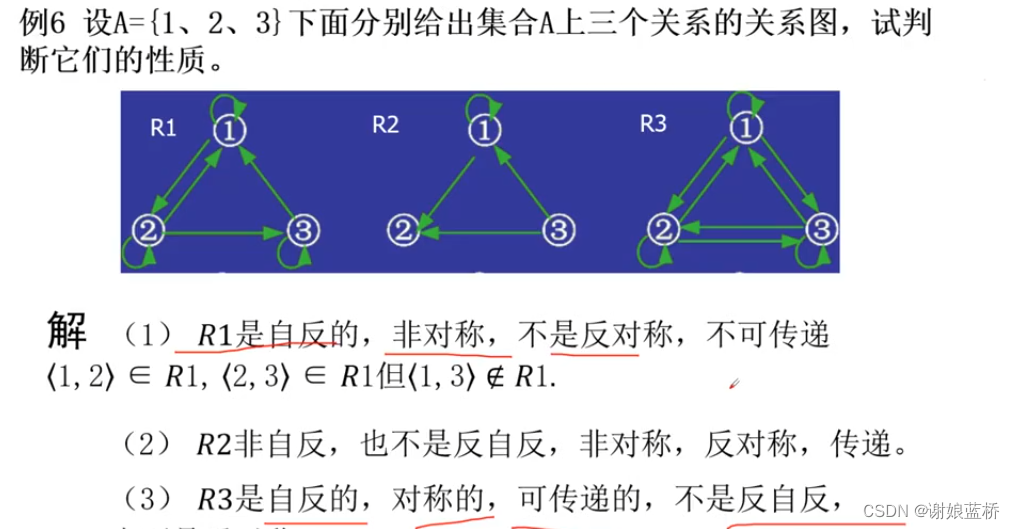
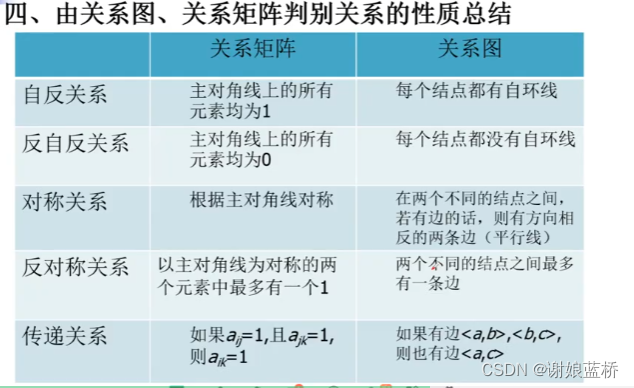
集合与关系

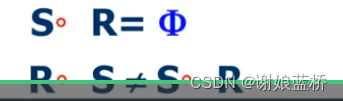
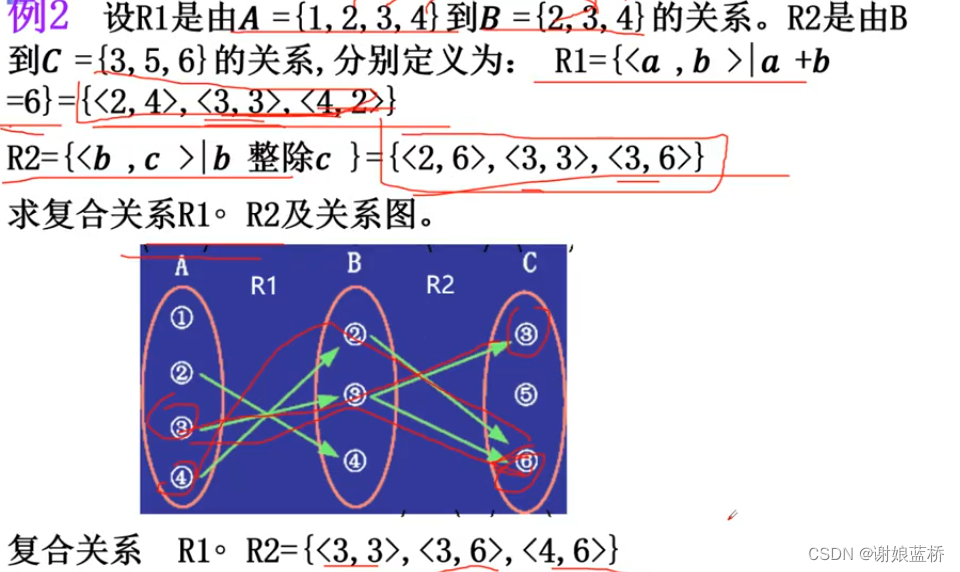
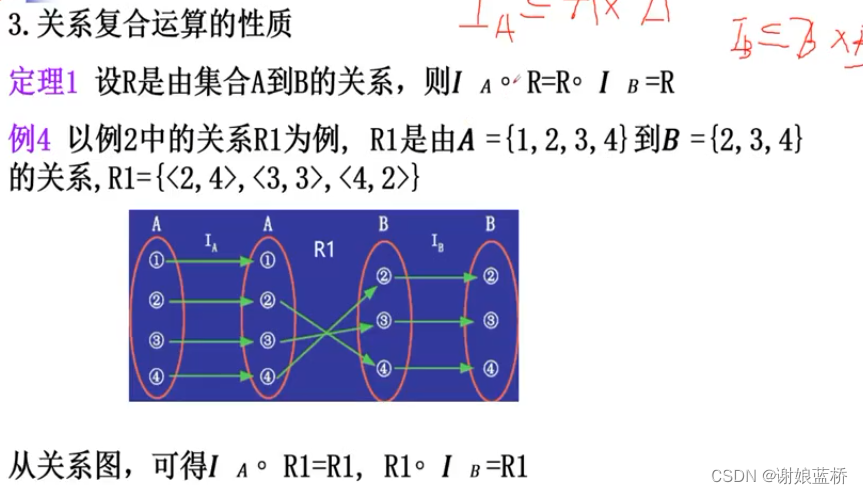
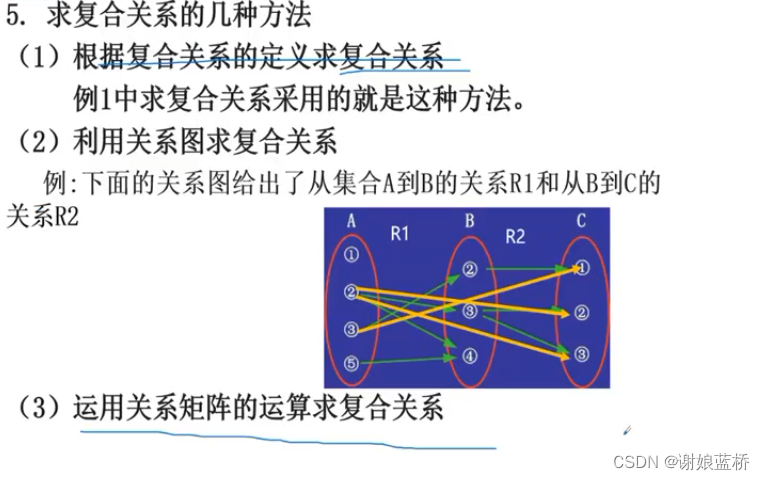
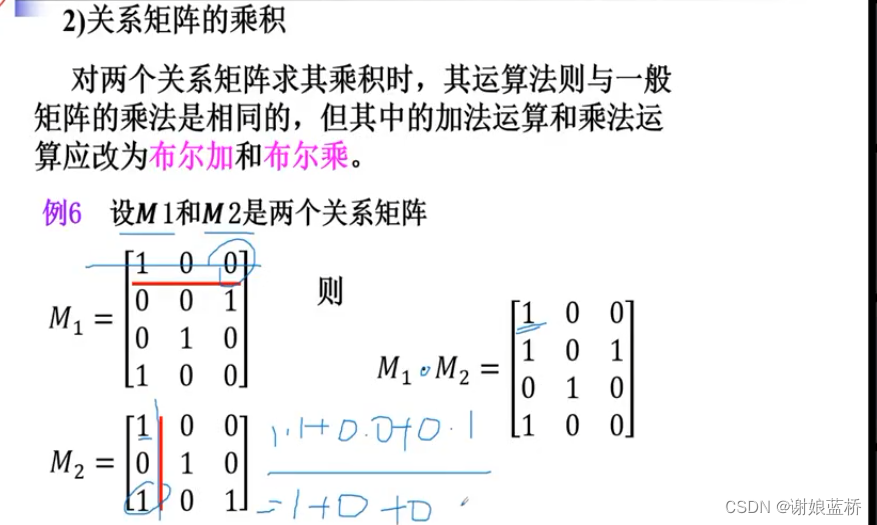
关系逆 就是矩阵的转置

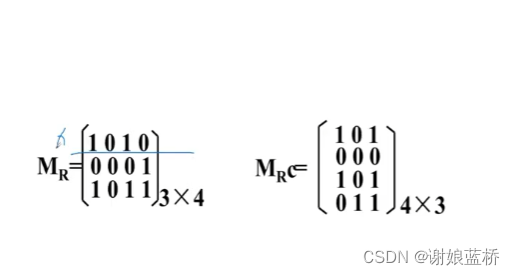
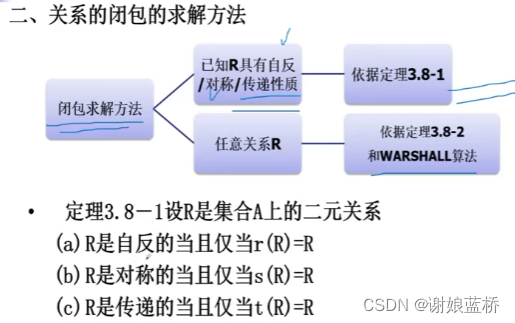
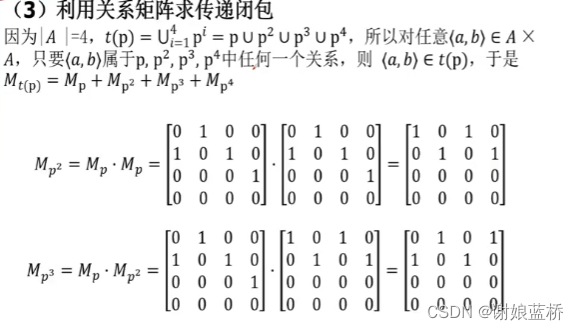
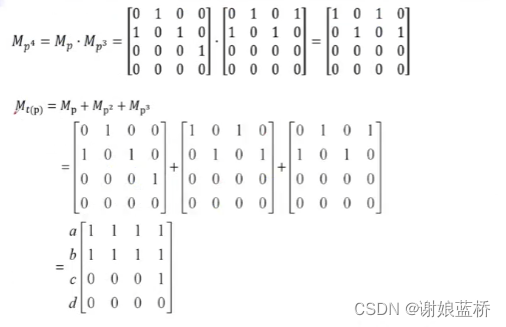
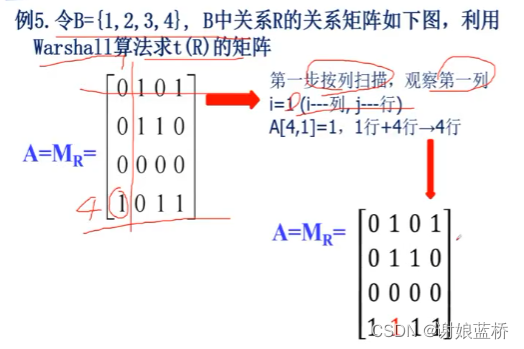
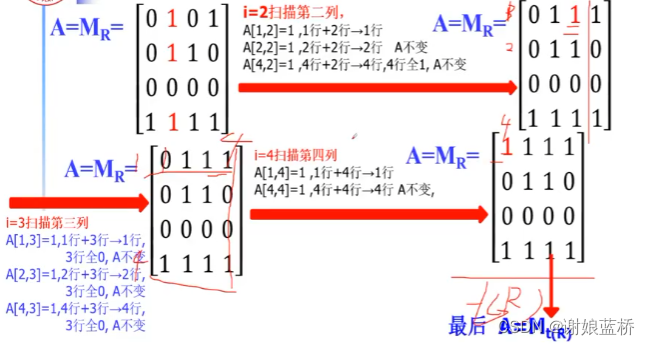
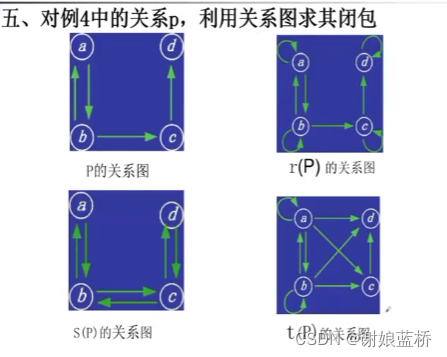
划分与覆盖

1.划分每一块非空
2.划分任意两块没有公共元素
3.A的划分耗尽所有A中的所有元素

等价关系 (取余、等)

等价关系具有 自反、对称、传递性质

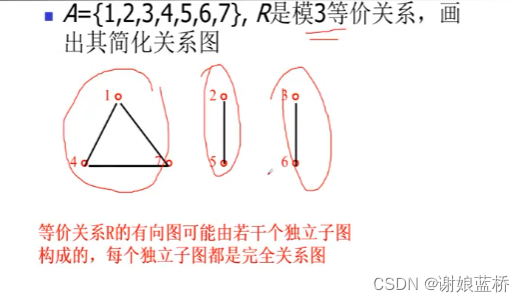
任意元素的等价类不是空集

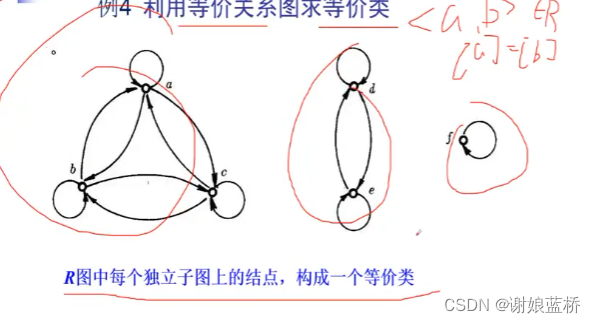
商集

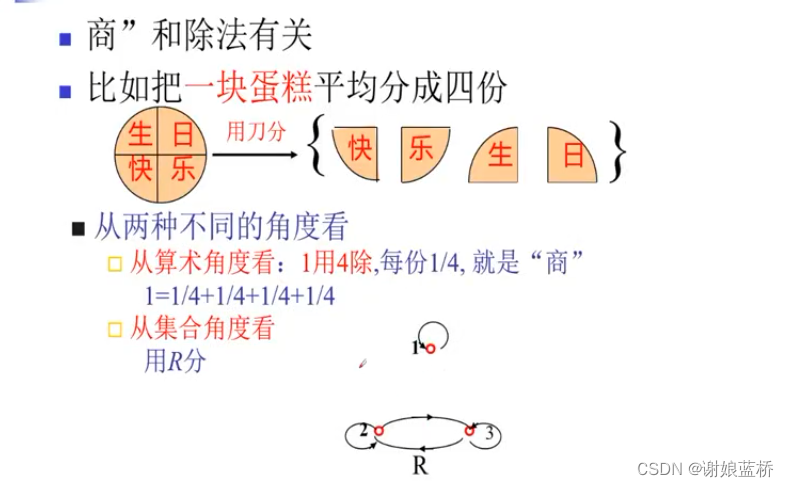
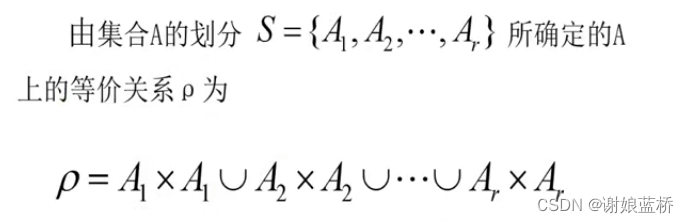
等价关系
证明等价关系
等价关系–等价类
商集
分块求等价关系

偏序关系—自反 反对称 传递(大于等于 小于等于 整除关系 包含 cover 幂集子集关系)

定义证明
特殊元素---->哈斯图

偏序关系的哈斯图

示例 （去除自反性、传递性的关系 去掉的元素对图的层次没有影响(每个节点之间有传递性)）
<A,$\le$>= { < 1 , 2 > , < 2 , 2 , > , < 2 , 4 > , < 1 , 4 > , < 4 , 4 > } \left\lbrace <1,2>,<2,2,>,<2,4>,<1,4>,<4,4>\right\rbrace {<1,2>,<2,2,>,<2,4>,<1,4>,<4,4>}

cov A = { < 1 , 2 > , < 2 , 4 > } \left\lbrace <1,2>,<2,4>\right\rbrace {<1,2>,<2,4>}

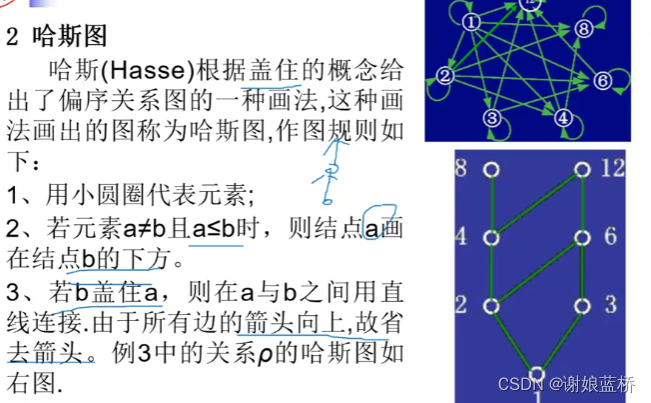
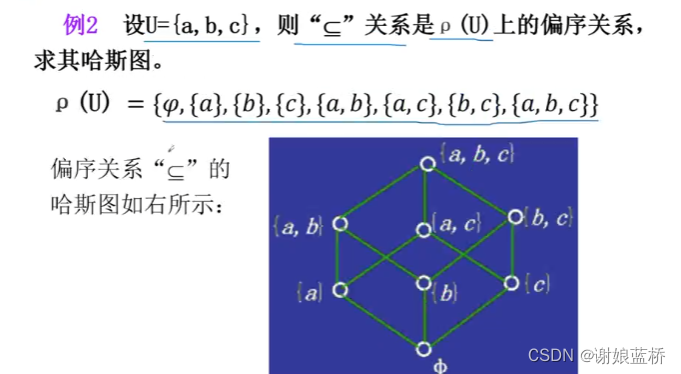
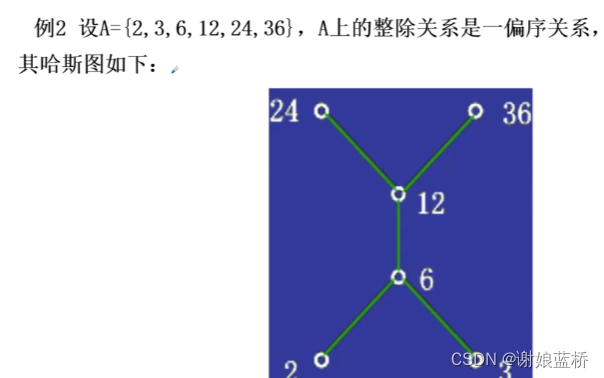
R= {<2,2>,<2,6>,<2,12>,<2,24>,<2,36>,
< 3,3>,< 3,6>,< 3,12>,< 3,24>,< 3,36>
<6,6>,<6,12>,<6,24>,<6,36>,
<12,12>,<12,24>,<12,36>
<24,24>
<36,36>}
去除 自反性 <2,2> < 3,3,> <6,6> <12,12> <24,24> <36,36>
去除传递 <2,12> <2,24> <2,36> <2,6>
< 3,12> < 3,24> < 3,36>

极大（小）元不唯一，则不存在 最大(元)

整除关系

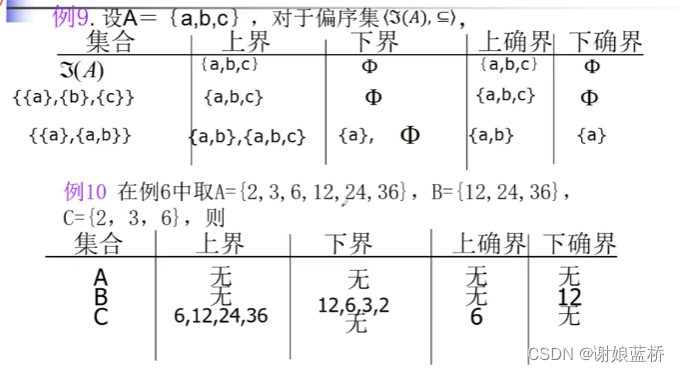
全序–线序 任意两个元素有偏序关系

良序 A中任意子集B 都有最小元素

每一个良序集都是全序

有限的全序时良序集

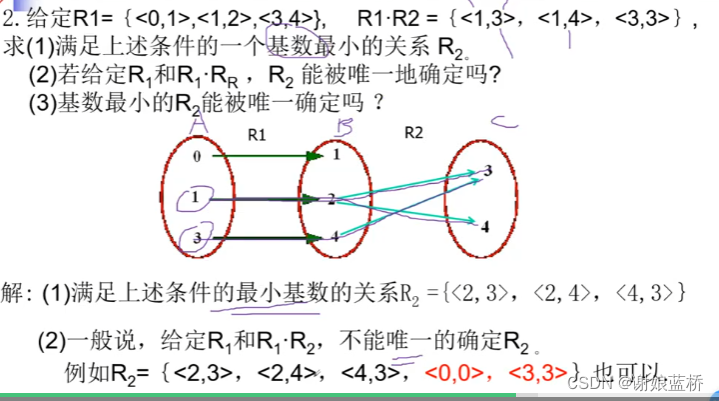
基数 关系数个数