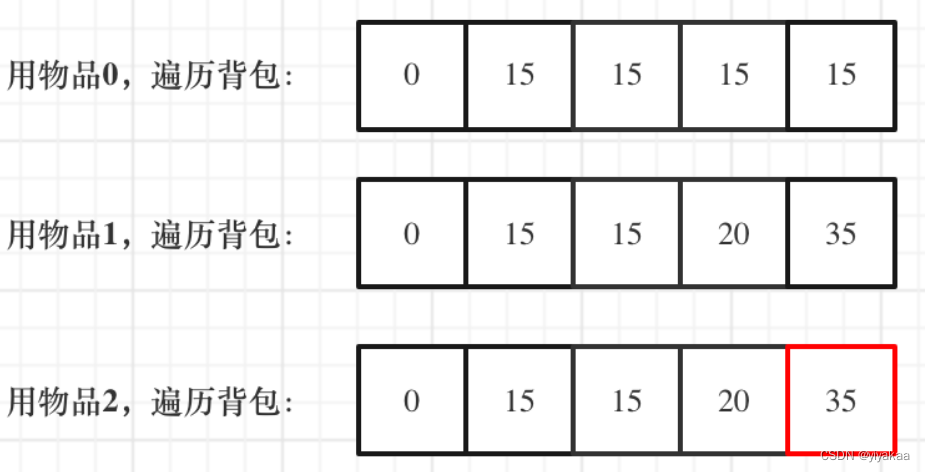
x.1 决策树前言

decision tree决策树是一种分类和回归的方法，本章只考虑在分类领域的使用。决策树使用了归纳法划分特征空间，以此来达到分类的目的。决策树不同于KNN中的kd树，它是多叉树，不是二叉树。决策树是一种概率模型。

决策树采用了if-then规则，路径上的内部节点是对特征的分类，叶节点对应着规则的结论（即分类的结果）。

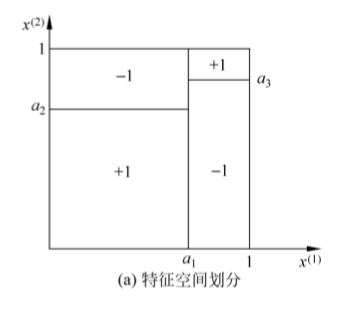
x.2 决策树学习算法

决策树的学习算法包括特征选择，决策树的生成与决策树的剪枝。其中核心要义是使用信息论的知识进行特征选择，决策树的生成就是使用了特征选择的方法更新下一节点（使用了特征增益是ID3算法，使用了特征增益比是C4.5算法），决策树的剪枝是为了避免过拟合的方法。

x.2.1 特征选择公式介绍

首先引入随机变量的entropy熵的定义，

entropy是用于表示随机变量不确定性的度量，当随机变量的entropy越小的时候，它就越规律，它的规律就越确定。当随机变量的取值等概率分布，即为均匀分布的时候，它的entropy就越大，随机变量就越不规律，它取那个值就越不确定，它的不确定性就越大，$entrop{y}_{max}={\log }_{2}n$。entropy的取值范围如下：

条件熵是指在已知随机变量X条件下，某一随机变量Y的不确定性，如下所示$X$可以指代一个特征，而$x_i$是该类特征的取值：

information gain 信息增益指的是通过得知特征X的信息而使类Y的信息不确定性减少的过程，它通过经验熵和条件熵的差值来表示。

x.2.2 特征选择例题

下面将以下列讲解：

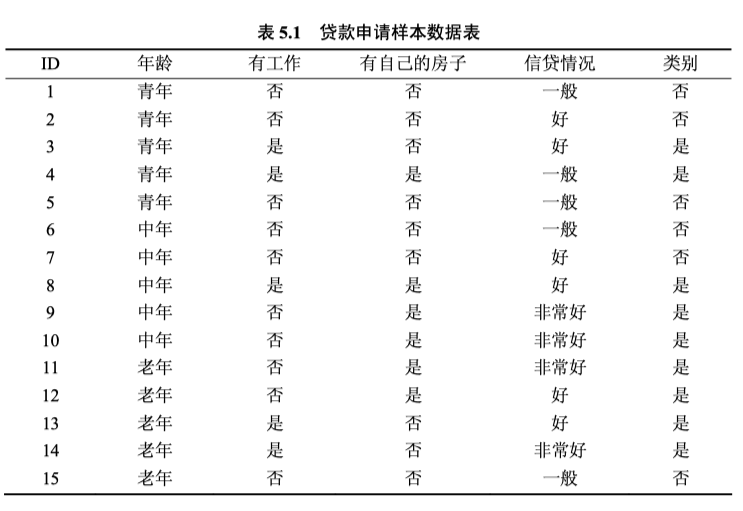
我们计算得到每个特征的信息增益，再根据选取信息增益的点作为根节点。循环直到确定所有特征。