1. 确定dp数组的定义

   在一维dp数组中，dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]。

2. 一维dp数组的递推公式

   dp[j]为 容量为j的背包所背的最大价值，那么如何推导dp[j]呢？

   dp[j]可以通过dp[j - weight[i]]推导出来，dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。

   dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。（也就是容量为j的背包，放入物品i了之后的价值即：dp[j]）

   此时dp[j]有两个选择，一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j]，即不放物品i，一个是取dp[j - weight[i]] + value[i]，即放物品i，指定是取最大的，毕竟是求最大价值，

所以递归公式为：

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

可以看出相对于二维dp数组的写法，就是把dp[i][j]中i的维度去掉了。

3. 一维dp数组如何初始化

   p[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该是0，因为背包容量为0所背的物品的最大价值就是0。

   那么dp数组除了下标0的位置，初始为0，其他下标应该初始化多少呢？

   递归公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

   dp数组在推导的时候一定是取价值最大的数，如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。

   这样才能让dp数组在递归公式的过程中取的最大的价值，而不是被初始值覆盖了。

   那么假设物品价值都是大于0的，所以dp数组初始化的时候，都初始为0就可以了。

4. 一维dp数组遍历顺序

代码如下：

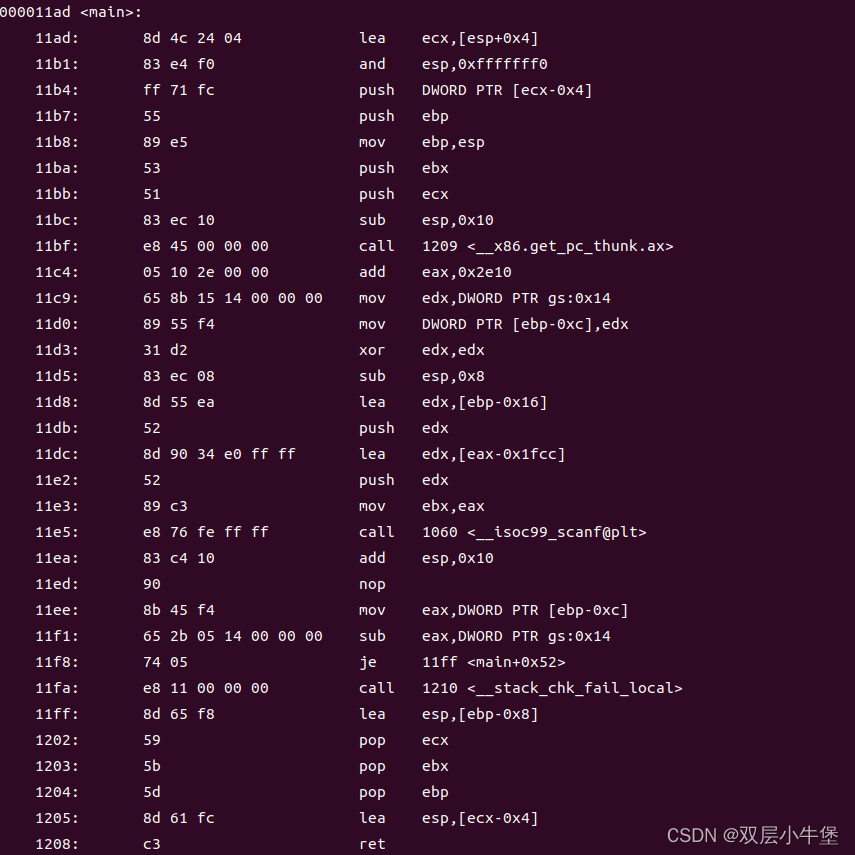
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

这里和二维dp的写法中，遍历背包的顺序是不一样的！二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。

倒序遍历是为了保证物品i只被放入一次！。但如果一旦正序遍历了，那么物品0就会被重复加入多次！

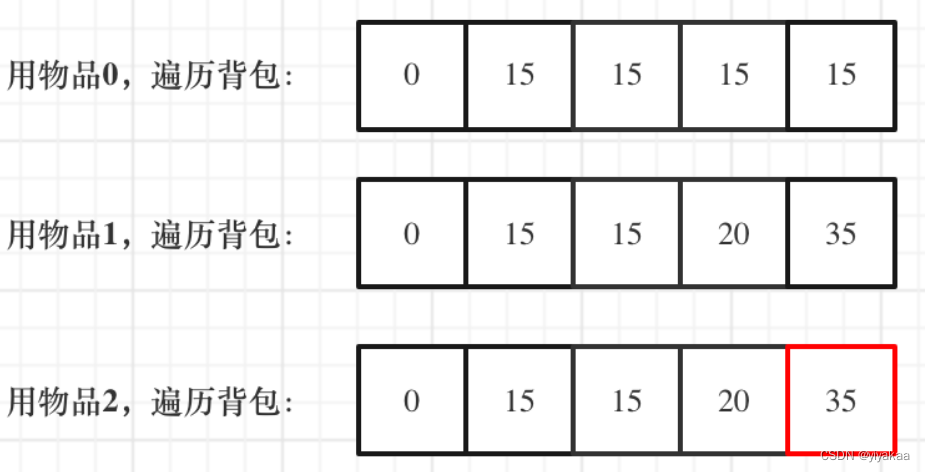
举例： 物品0的重量weight[0] = 1，价值value[0] = 15

如果正序遍历

dp[1] = dp[1 - weight[0]] + value[0] = 15

dp[2] = dp[2 - weight[0]] + value[0] = 30

此时dp[2]就已经是30了，意味着物品0，被放入了两次，所以不能正序遍历。

为什么倒序遍历，就可以保证物品只放入一次呢？

倒序就是先算dp[2]

dp[2] = dp[2 - weight[0]] + value[0] = 15 （dp数组已经都初始化为0）

dp[1] = dp[1 - weight[0]] + value[0] = 15

所以从后往前循环，每次取得状态不会和之前取得状态重合，这样每种物品就只取一次了。

那么问题又来了，为什么二维dp数组历的时候不用倒序呢？

因为对于二维dp，dp[i][j]都是通过上一层即dp[i - 1][j]计算而来，本层的dp[i][j]并不会被覆盖！

代码中是先遍历物品嵌套遍历背包容量，顺序不能颠倒！！！

5. 推导dp数组

void test_1_wei_bag_problem() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;

    // 初始化
    vector<int> dp(bagWeight + 1, 0);
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;
}

int main() {
    test_1_wei_bag_problem();
}

学习自：代码随想录。