毕业论文写完了。找点事干干。
佛系更新。
这是一门讲述
- 什么是计算?
- 什么能被计算?
- 怎么高效计算?
的哲学、数学和工程问题的课程。
主要包括:
-
有限状态机(Finite Avtomata):简单的模型。
-
可计算理论。
-
计算复杂性理论:被时间和空间复杂度约束着的模型。
这门课涉及的(数学)证明主要将阐述证明的想法。
讲明白idea比写一堆细节重要(又不是上数学分析课
确定性有限自动机(Deterministic Finite Avtomata)
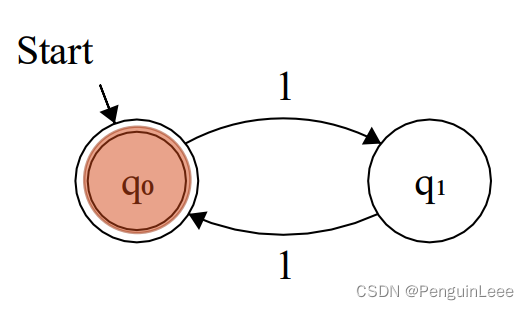
一个简单的例子:计算一个全1字符串里有奇数个1还是偶数个1。
状态机从
q
0
q_0
q0开始。给定一串(有限长度的)111…111,每一次读一个字符(1),根据此时状态的转移规则进行状态转移,直到读完为止。
DFA详解:
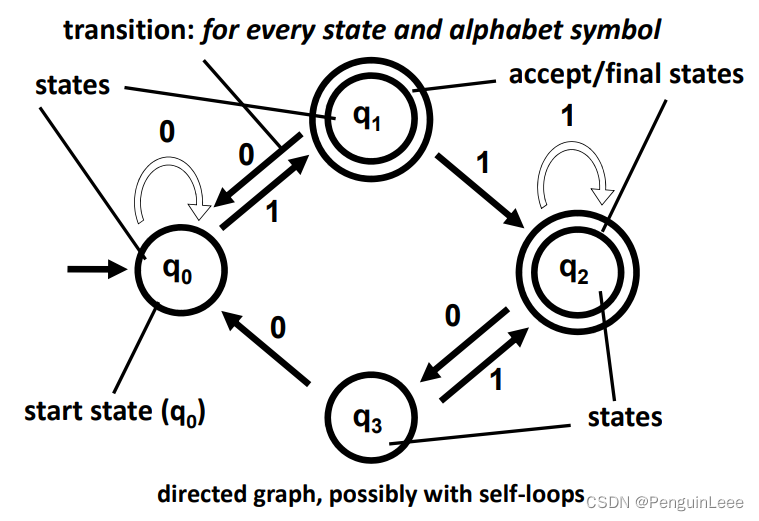
有一个入口(初始状态)和一个字符串。在字符满足条件的情况下,需要从状态A转化到状态B。有终止状态(用同心圆表述)。
如果从初始状态开始,状态遵循字符串中字符的顺序和状态转移逻辑进行转化,最后停在终止状态(同心圆状态),表示DFA接受这个字符串,否则,DFA拒绝这个字符串。
更正式的定义如下:

一个DFA被定义为一个五元组。状态集、字符集
Σ
\Sigma
Σ(比如{0, 1}、英文字母表、UTF-8)、起始状态、终止状态集、状态转移函数。
语言(Language):语言是 2 Σ 2^\Sigma 2Σ的子集。比如, Σ \Sigma Σ是英文字母表,语言L可以是英语中所有a开头的单词,或者所有包含sh*t的单词。
或者说,语言是一个接受一个字符串作为输入、输出0或1的函数。
L(M) = 由确定性有限状态机M定义的语言。
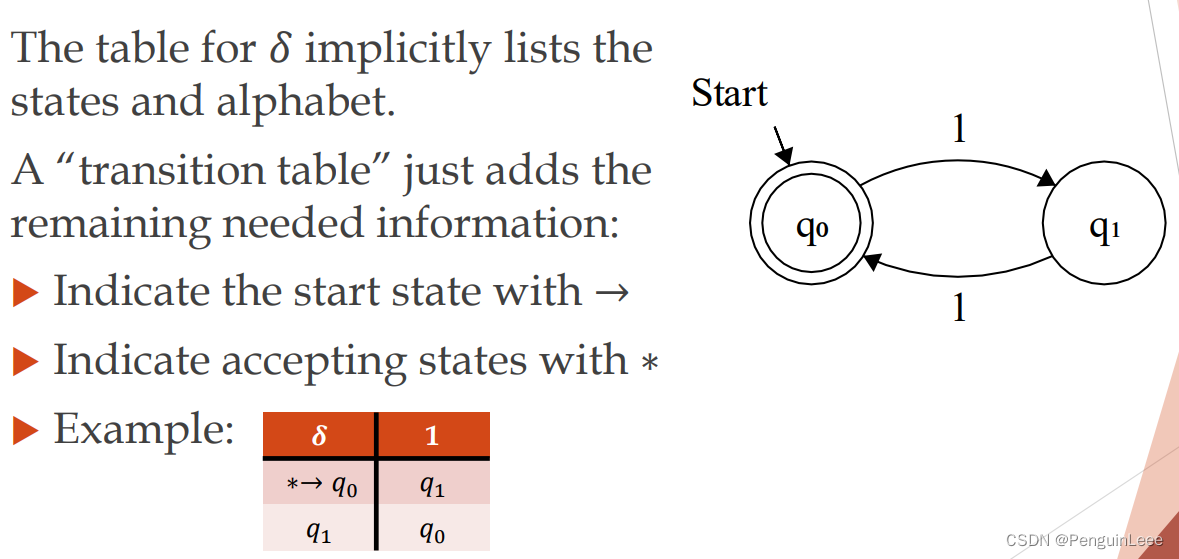
注意这个
∗
→
q
0
* \rightarrow q_0
∗→q0,表示:
q
0
q_0
q0是一个初始状态,也是终止状态。
我们也可以对DFA的状态转移函数进行拓展,通过递归的方式定义输入为一个字符串的时候的“拓展”状态转移函数:

对有限自动机的证明:
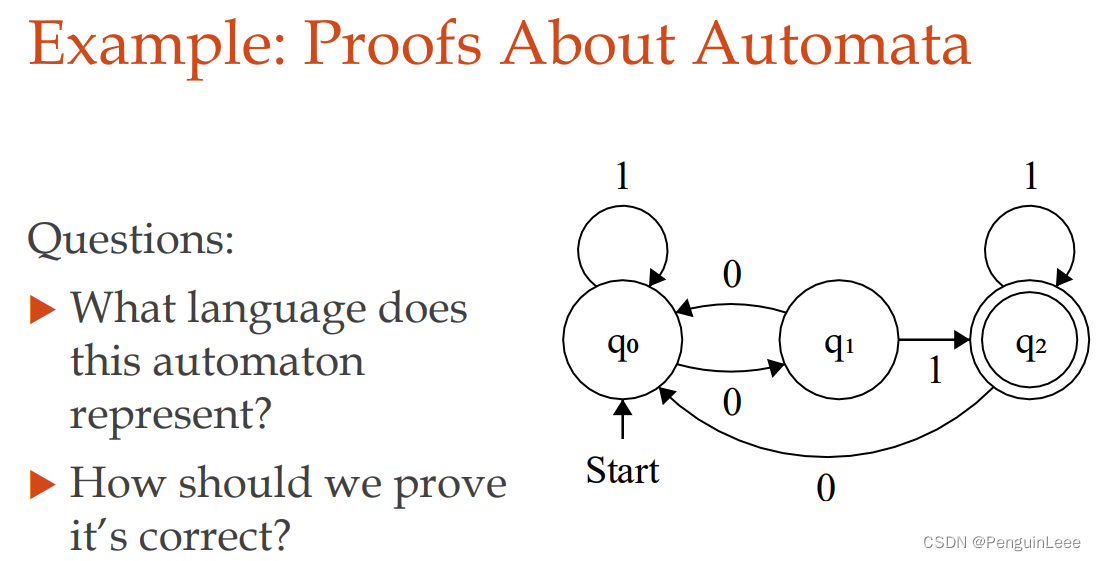
这个自动机说了什么?(或者说,哪些语法是匹配上述自动机的?)
怎么证明我们得出的语法是对的?
上面这个自动机匹配的是有奇数个0,并且结尾为1的字符串。
证明:
q
0
q_0
q0状态:有偶数个0
q
1
q_1
q1状态:有奇数个0,且结尾为0
q
2
q_2
q2状态:有奇数个0,且结尾为1
可以用数学归纳法解决剩下的事情。
定义:语言L’是常规(regular)的,如果L’可以用DFA来描述。即存在M使得:L’ = L(M)。
常规语言的求并定理:
给定两个正规语言
L
i
,
i
=
1
,
2
L_i, i=1,2
Li,i=1,2。
L
1
∪
L
2
=
w
∣
w
∈
L
i
,
i
=
1
∣
∣
i
=
2
L_1 \cup L_2 = {w| w \in L_i, i=1 || i=2 }
L1∪L2=w∣w∈Li,i=1∣∣i=2。
于是,
L
1
∪
L
2
L_1 \cup L_2
L1∪L2也是常规的。
证明思路:主要考虑两个DFA的并行运算。对于正规语言 L i L_i Li,我们考虑对应的DFA,分别记为 M i M_i Mi。分别考虑 M i M_i Mi的状态 Q i Q_i Qi,作笛卡尔积 Q 1 × Q 2 Q_1 \times Q_2 Q1×Q2。然后构造符合两个DFA的转移规则即可。
常规语言的求交定理:
给定两个正规语言
L
i
,
i
=
1
,
2
L_i, i=1,2
Li,i=1,2。
L
1
∩
L
2
=
w
∣
w
∈
L
i
,
i
=
1
&
&
i
=
2
L_1 \cap L_2 = {w| w \in L_i, i=1 \&\& i=2 }
L1∩L2=w∣w∈Li,i=1&&i=2。
于是,
L
1
∩
L
2
L_1 \cap L_2
L1∩L2也是常规的。
证明思路:仍然是考虑两个DFA的并行运算。
求补定理:
给定正规语言
L
L
L,
L
c
L^c
Lc也是正规语言。
证明:把终端集和非终端集翻过来就行了。
语言的反转 L R L^R LR。比如: 0 , 10 , 110 , 0101 R = 0 , 01 , 011 , 1010 {0, 10, 110, 0101}^R = {0, 01, 011, 1010} 0,10,110,0101R=0,01,011,1010。
正规语言的反转定理。
反转后的正规语言也是正规语言。对于每一个可以从右往左读的、可被DFA描述的语言,都有从左往右读的、可被DFA描述的语言相对应。
但是怎么证明呢?
我们希望:给定DFA
M
M
M,对应的正规语言是
L
L
L,能够构造一个
M
R
M^R
MR,使得
M
R
M^R
MR接受
w
R
w^R
wR当且仅当
M
M
M接受
w
w
w。
一个简单的尝试:把M的所有箭头和集合状态都反过来。但是按照这种操作方式,会遇到问题:
M R M^R MR并不永远是DFA。
比如,可能有很多个初始状态,对于一个给定的状态和输入,可能有多个(或者没有)转移规则。
于是我们引入:
非确定性有限状态机(Non-Deterministic Finite Avtomata)
首先,我们考虑一个DFA:
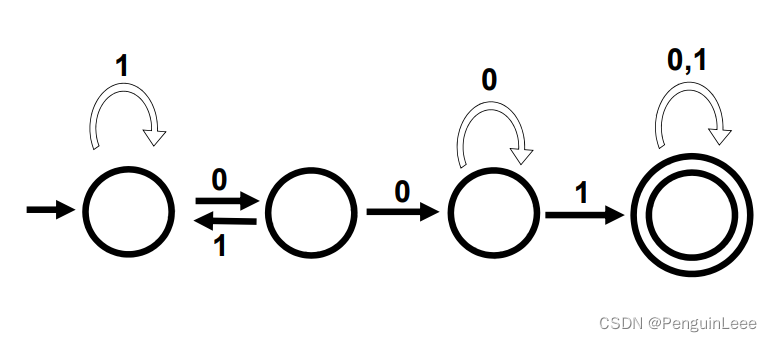
这个DFA
M
M
M接受包含001的字符串。
我们考虑 M R M^R MR。
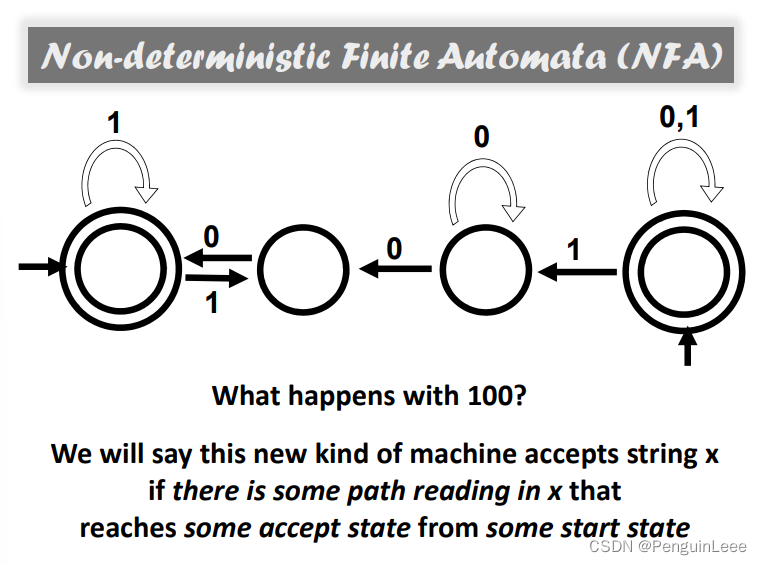
在上图这个新automaton中,对于一个字符串,如果存在通路使得状态能到最终状态,那么我们认为逻辑被接受。
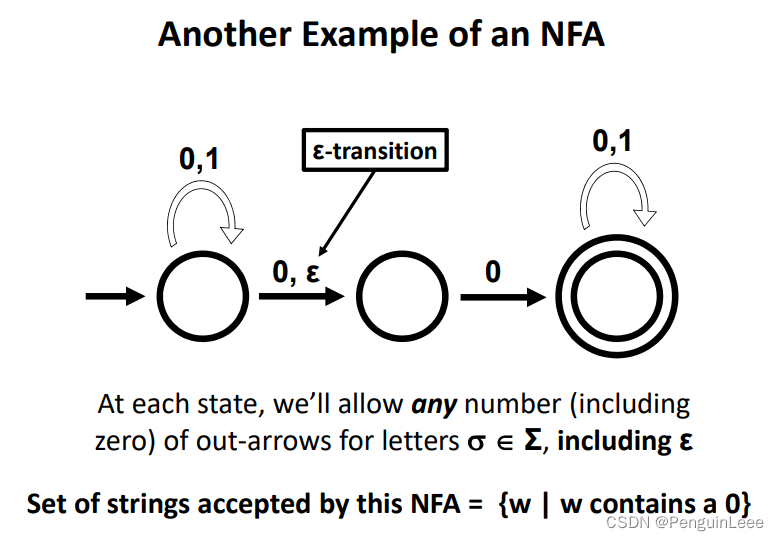
另一种类型的NFA:
ϵ
\epsilon
ϵ-NFA。这里的
ϵ
\epsilon
ϵ通路意味着空跳,可以在不接受字符的情况下转移状态。
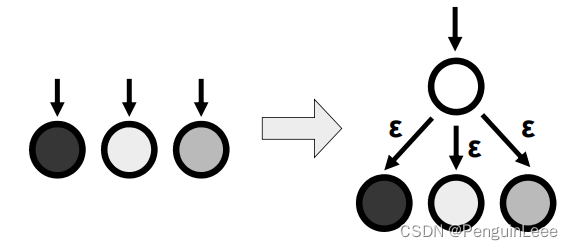
比如:在有多个起始状态的情况下,可以这么表述:
NFA里的状态转移函数 δ ( q , c h a r ) \delta(q, char) δ(q,char)有可能返回的是一个状态的集合。当然这个集合也有可能是空集。
对于DFA:
- 在给定状态和输入的时候,DFA的转移函数值是确定的(Deterministic)。
- DFA接受一个字符串,当且仅当这个字符串将使DFA到达一个终点状态。
对于NFA:
- 对于一个给定的字符串,NFA可能会从很多不同的路中选一条。
- NFA接受字符串,当且仅当这个字符串“可能”使NFA到达一个终点状态。
DFA里,扩张状态转移函数 δ ^ ( s t a t e , s t r i n g ) \hat \delta(state, string) δ^(state,string)可以吃下一个字符串。
在NFA里,也可以定义这样的操作。如果NFA有初始状态 q q q,那么字符串 x x x符合语法当且仅当 δ ^ ( q , x ) ∩ F ≠ ∅ \hat \delta(q, x) \cap F \neq \varnothing δ^(q,x)∩F=∅。其中,F是终止状态集。
对NFA的递归定义:
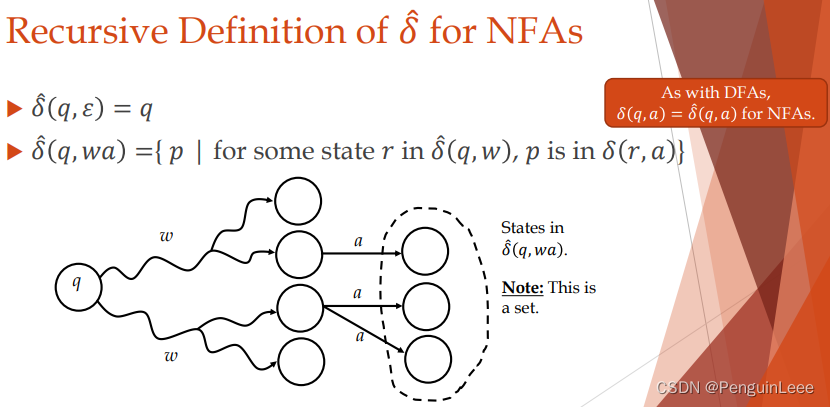
对NFA中状态集合的定义。假设
P
P
P是一个状态集合,那么
δ
(
P
,
a
)
=
∪
q
∈
P
δ
(
q
,
a
)
\delta (P, a) = \cup_{q \in P} \delta (q, a)
δ(P,a)=∪q∈Pδ(q,a)
NFA的一个例子:
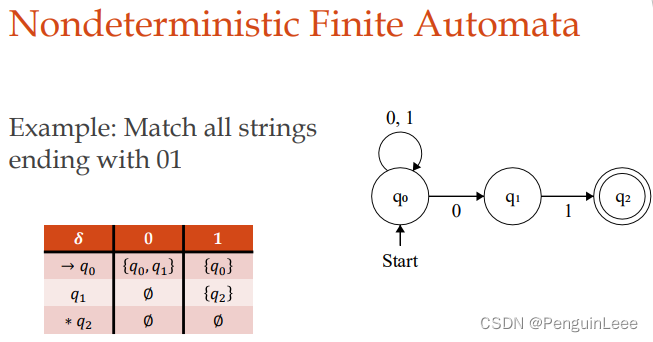
给定字符串str = 10101,上述NFA如何执行呢?
- F = q 2 F = q_2 F=q2
- δ ^ ( q 0 , 10101 ) = q 0 , q 2 \hat \delta(q_0, 10101) = {q_0, q_2} δ^(q0,10101)=q0,q2
-
q
0
,
q
2
∩
F
=
q
2
{q_0, q_2} \cap F = {q_2}
q0,q2∩F=q2
于是字符串10101符合上述NFA。
一般来说,NFA用起来比DFA更方便。
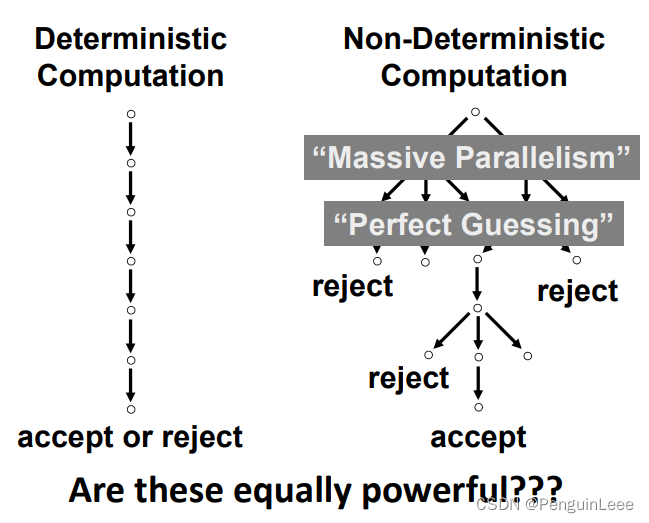
NFA和DFA是等价的吗?
是的。
定理:对于任意NFA N N N,都存在一个DFA M M M使得 L ( M ) = L ( N ) L(M)=L(N) L(M)=L(N)。
具体想法:对于NFA,我们可以直接构造DFA,通过构造状态集的幂集。