周赛345（模拟、分类讨论、DFS求完全联通分量）

news2024/12/1 2:35:35

文章目录

  • 周赛345
    • [2682. 找出转圈游戏输家](https://leetcode.cn/problems/find-the-losers-of-the-circular-game/)
      • 模拟
    • [2683. 相邻值的按位异或](https://leetcode.cn/problems/neighboring-bitwise-xor/)
      • 方法一：分类讨论（反向思考）
      • 方法二：找规律、推公式
    • [2684. 矩阵中移动的最大次数](https://leetcode.cn/problems/maximum-number-of-moves-in-a-grid/)(求最大路径长度)
      • 方法一：DFS（递归==> 记忆化搜索）
      • 方法二：记忆化转DP
      • 方法三：BFS
      • 🎉相似题目：网格图 DP
    • [2685. 统计完全连通分量的数量](https://leetcode.cn/problems/count-the-number-of-complete-components/)
      • 方法一：DFS
      • 方法二：并查集

周赛345

2682. 找出转圈游戏输家

难度简单0收藏分享切换为英文接收动态反馈

n 个朋友在玩游戏。这些朋友坐成一个圈，按 顺时针方向 从 1 到 n 编号。从第 i 个朋友的位置开始顺时针移动 1 步会到达第 (i + 1) 个朋友的位置（1 <= i < n），而从第 n 个朋友的位置开始顺时针移动 1 步会回到第 1 个朋友的位置。

游戏规则如下：

第 1 个朋友接球。

  • 接着，第 1 个朋友将球传给距离他顺时针方向 k 步的朋友。
  • 然后，接球的朋友应该把球传给距离他顺时针方向 2 * k 步的朋友。
  • 接着，接球的朋友应该把球传给距离他顺时针方向 3 * k 步的朋友，以此类推。

换句话说，在第 i 轮中持有球的那位朋友需要将球传递给距离他顺时针方向 i * k 步的朋友。

当某个朋友第 2 次接到球时，游戏结束。

在整场游戏中没有接到过球的朋友是 输家 。

给你参与游戏的朋友数量 n 和一个整数 k ，请按升序排列返回包含所有输家编号的数组 answer 作为答案。

示例 1：

输入：n = 5, k = 2
输出：[4,5]
解释：以下为游戏进行情况：
1）第 1 个朋友接球，第 1 个朋友将球传给距离他顺时针方向 2 步的玩家 —— 第 3 个朋友。
2）第 3 个朋友将球传给距离他顺时针方向 4 步的玩家 —— 第 2 个朋友。
3）第 2 个朋友将球传给距离他顺时针方向 6 步的玩家 —— 第 3 个朋友。
4）第 3 个朋友接到两次球，游戏结束。

示例 2：

输入：n = 4, k = 4
输出：[2,3,4]
解释：以下为游戏进行情况：
1）第 1 个朋友接球，第 1 个朋友将球传给距离他顺时针方向 4 步的玩家 —— 第 1 个朋友。
2）第 1 个朋友接到两次球，游戏结束。

提示：

  • 1 <= k <= n <= 50

模拟

class Solution {
    public int[] circularGameLosers(int n, int k) {
        int[] vis = new int[n];
        vis[0] = 1;
        int cur = 0, t = 1;
        while(true){
            cur = (cur + t * k) % n;
            if(vis[cur] == 1) break;
            vis[cur] = 1;
            t += 1;
        }
        List<Integer> res = new ArrayList<>();
        for(int i = 0; i < n; i++){
            if(vis[i] == 0)
                res.add(i+1);
        }
        return res.stream().mapToInt(Integer::intValue).toArray();
    }
}

时间复杂度：O(n)

2683. 相邻值的按位异或

难度中等0

下标从 0 开始、长度为 n 的数组 derived 是由同样长度为 n 的原始 二进制数组 original 通过计算相邻值的 **按位异或（⊕）**派生而来。

特别地，对于范围 [0, n - 1] 内的每个下标 i ：

  • 如果 i = n - 1 ，那么 derived[i] = original[i] ⊕ original[0]
  • 否则 derived[i] = original[i] ⊕ original[i + 1]

给你一个数组 derived ，请判断是否存在一个能够派生得到 derived 的 有效原始二进制数组 original 。

如果存在满足要求的原始二进制数组，返回 true ；否则，返回 false 。

  • 二进制数组是仅由 0 和 1 组成的数组。

示例 1：

输入：derived = [1,1,0]
输出：true
解释：能够派生得到 [1,1,0] 的有效原始二进制数组是 [0,1,0] ：
derived[0] = original[0] ⊕ original[1] = 0 ⊕ 1 = 1 
derived[1] = original[1] ⊕ original[2] = 1 ⊕ 0 = 1
derived[2] = original[2] ⊕ original[0] = 0 ⊕ 0 = 0

示例 2：

输入：derived = [1,1]
输出：true
解释：能够派生得到 [1,1] 的有效原始二进制数组是 [0,1] ：
derived[0] = original[0] ⊕ original[1] = 1
derived[1] = original[1] ⊕ original[0] = 1

示例 3：

输入：derived = [1,0]
输出：false
解释：不存在能够派生得到 [1,0] 的有效原始二进制数组。

提示：

  • n == derived.length
  • 1 <= n <= 105
  • derived 中的值不是 0 就是 1 。

方法一：分类讨论（反向思考）

思路启发：2437. 有效时间的数目，由于二进制数组是仅由 0 和 1 组成的数组。那么原数组只能有两种情况，a[0] = 0 和 a[0] = 1，分别构造这两原数组

class Solution {
    public boolean doesValidArrayExist(int[] derived) {
        // 两种情况，a[0] = 0 , a[0] = 1 分别尝试能否构成derived数组
        int n = derived.length;
        int[] ori = new int[n];
        // 先构造a[0] = 0的情况，根据derived[i]取值判断a[i+1]的取值情况，最后根据a[n-1]和a[0]的取值是否合法判断是否为答案
        for(int i = 0; i < n; i++){
            if(i != n-1){
                if(derived[i] == 1){
                    ori[i+1] = 1 - ori[i];
                }else{
                    ori[i+1] = ori[i];
                }
            }else{
                if((derived[i] == 1 && ori[i] != ori[0]) || 
                    (derived[i] == 0 && ori[i] == ori[0]))
                    return true;
            }
        }
        ori = new int[n];
        ori[0] = 1;
        for(int i = 0; i < n; i++){
            if(i != n-1){
                if(derived[i] == 1){
                    ori[i+1] = 1 - ori[i];
                }else{
                    ori[i+1] = ori[i];
                }
            }else{
                if((derived[i] == 1 && ori[i] != ori[0]) || 
                    (derived[i] == 0 && ori[i] == ori[0]))
                    return true;
            }
        }
        return false;
    }
}

方法二：找规律、推公式

class Solution {
    /**
    找规律：推公式
    由 a ^ a = 0
       a ^ b = c ，两边同时异或 a 得到 b = c ^ a

    公式一：derived[i] = original[i] ⊕ original[i + 1]
    a[0]
    a[1] = b[0] ^ a[0]
    a[2] = b[1] ^ a[1] = b[1] ^ b[0] ^ a[0]
    a[3] = b[2] ^ b[1] ^ b[0] ^ a[0]
    公式二：如果 i = n - 1 ，那么 derived[i] = original[i] ⊕ original[0]
    a[3] ^ a[0] = b[3]

    两个公式合起来（左边异或左边，右边异或右边）
    a[0] = b[2] ^ b[1] ^ b[0] ^ a[0] ^ b[3]
    ==> 0 = b[3] ^ b[2] ^ b[1] ^ b[0]
    判断所有数异或和是否为0
     */
    public boolean doesValidArrayExist(int[] derived) {
        int i = 0;
        for(int d : derived) i ^= d;
        return i == 0;
    }
}

时间复杂度：O(n)

2684. 矩阵中移动的最大次数(求最大路径长度)

难度中等0收藏分享切换为英文接收动态反馈

给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ，矩阵由若干 正 整数组成。

你可以从矩阵第一列中的 任一 单元格出发，按以下方式遍历 grid ：

  • 从单元格 (row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值 严格 大于当前单元格的单元格。

返回你在矩阵中能够 移动 的 最大 次数。

示例 1：

img

输入：grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
输出：3
解释：可以从单元格 (0, 0) 开始并且按下面的路径移动：
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
可以证明这是能够移动的最大次数。

示例 2：

输入：grid = [[3,2,4],[2,1,9],[1,1,7]]
输出：0
解释：从第一列的任一单元格开始都无法移动。

提示：

  • m == grid.length
  • n == grid[i].length
  • 2 <= m, n <= 1000
  • 4 <= m * n <= 105
  • 1 <= grid[i][j] <= 106

方法一：DFS（递归==> 记忆化搜索）

class Solution {
    int[][] dirts = {{-1, 1}, {0, 1}, {1, 1}};
    int[][] grid;
    int m, n;
    int[][] cache; 
    public int maxMoves(int[][] grid) {
        // dfs求最大路径长
        int ans = 0;
        m = grid.length; n = grid[0].length;
        cache = new int[m][n];
        for(int i = 0; i < m; i++)
            Arrays.fill(cache[i], -1);
        this.grid = grid;
        for(int i = 0; i < m; i++){
            ans = Math.max(ans, dfs(i, 0));
        }
        return ans;
    }

    public int dfs(int i, int j){
        int ans = 0;
        if(cache[i][j] >= 0) return cache[i][j];
        for(int[] d : dirts){
            int x = i + d[0], y = j + d[1];
            if(x < 0 || x >= m || y < 0 || y >= n)
                continue;
            if(grid[x][y] > grid[i][j])
                ans = Math.max(ans, dfs(x, y) + 1);
        }
        return cache[i][j] = ans;
    }
}

方法二：记忆化转DP

class Solution {
    public int maxMoves(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        // 定义f[i][j]表示从f[i][j]开始按照要求移动能走的最大次数
        int[][] f = new int[m][n];
        // 思考清楚递推顺序
        // f[i][j] 需要 f[i-1][j+1] f[i][j+1] f[i+1][j+1]，因此要先枚举j再枚举i
        for(int j = n-2; j >= 0; j--){
            for(int i = 0; i < m; i++){
                for (int k = Math.max(i - 1, 0); k < Math.min(i + 2, m); k++)
                    if (grid[k][j + 1] > grid[i][j])
                        f[i][j] = Math.max(f[i][j], f[k][j + 1] + 1);
            }
        }
        int ans = 0;
        for(int i = 0; i < m; i++)
            ans = Math.max(ans, f[i][0]);
        return ans;
    }
}
/**
class Solution:
    def maxMoves(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        @cache
        def dfs(i: int, j: int) -> int:
            if j == n - 1:
                return 0
            res = 0
            for k in i - 1, i, i + 1:
                if 0 <= k < m and grid[k][j + 1] > grid[i][j]:
                    res = max(res, dfs(k, j + 1) + 1)
            return res
        return max(dfs(i, 0) for i in range(m))
 */

方法三：BFS

class Solution:
    def maxMoves(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        q = range(m) # 记录行号
        print(q) # range(0, 4)
        vis = [-1] * m
        # 从左往右遍历，每一轮向右搜索一列
        # 只要能搜索到第 k 列，那么答案至少为k，当队列长度=0时，表示走不到第 k 列了，答案为k-1
        for j in range(n-1):
            tmp = q
            q = []
            for i in tmp:
                for k in i-1, i, i+1:
                    if 0 <= k < m and vis[k] != j and grid[k][j + 1] > grid[i][j]:
                        vis[k] = j # 时间戳标记，避免重复创建 vis 数组
                        q.append(k)
            if len(q) == 0:
                return j
        return n-1

🎉相似题目：网格图 DP

https://leetcode.cn/problems/maximum-number-of-moves-in-a-grid/submissions/

  • 62. 不同路径
  • 63. 不同路径 II
  • 64. 最小路径和
  • 120. 三角形最小路径和
  • 931. 下降路径最小和
  • 2435. 矩阵中和能被 K 整除的路径

2685. 统计完全连通分量的数量

难度中等2

给你一个整数 n 。现有一个包含 n 个顶点的 无向 图，顶点按从 0 到 n - 1 编号。给你一个二维整数数组 edges 其中 edges[i] = [ai, bi] 表示顶点 ai 和 bi 之间存在一条 无向 边。

返回图中 完全连通分量 的数量。

如果在子图中任意两个顶点之间都存在路径，并且子图中没有任何一个顶点与子图外部的顶点共享边，则称其为 连通分量 。

如果连通分量中每对节点之间都存在一条边，则称其为 完全连通分量 。

示例 1：

img

输入：n = 6, edges = [[0,1],[0,2],[1,2],[3,4]]
输出：3
解释：如上图所示，可以看到此图所有分量都是完全连通分量。

示例 2：

img

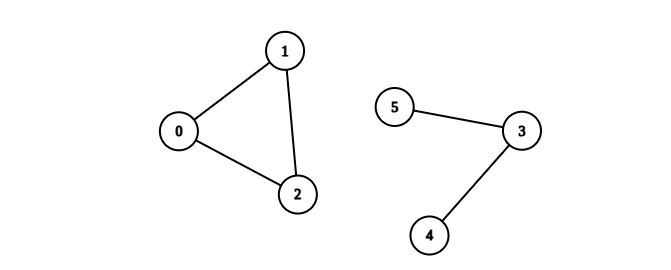
输入：n = 6, edges = [[0,1],[0,2],[1,2],[3,4],[3,5]]
输出：1
解释：包含节点 0、1 和 2 的分量是完全连通分量，因为每对节点之间都存在一条边。
包含节点 3 、4 和 5 的分量不是完全连通分量，因为节点 4 和 5 之间不存在边。
因此，在图中完全连接分量的数量是 1 。

提示：

  • 1 <= n <= 50
  • 0 <= edges.length <= n * (n - 1) / 2
  • edges[i].length == 2
  • 0 <= ai, bi <= n - 1
  • ai != bi
  • 不存在重复的边

方法一：DFS

class Solution {
    List<Integer>[] g;
    boolean[] vis, tmp;
    public int countCompleteComponents(int n, int[][] edges) {
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for(int[] e : edges){
            g[e[0]].add(e[1]);
            g[e[1]].add(e[0]);
        }
        int ans = 0;
        vis = new boolean[n];
        tmp = new boolean[n];
        // 遍历每一个连通分量
        for(int i = 0; i < n; i++){
            if(vis[i]) continue;
            vis[i] = true;  
            // 统计每一个联通分量 点的个数 和 边的个数，边的个数应该为节点数 的 n(n-1) / 2
            // 统计连通分类个数
            tmp[i] = true;
            int num = dfsnum(i);
            int edge = dfs(i) / 2;
            if(edge == num * (num-1) / 2)
                ans += 1;
        }
        return ans;
    }
	// dfs求连通块节点个数
    public int dfsnum(int x){
        int res = 1;
        for(int y : g[x]){
            if(!tmp[y]){
                tmp[y] = true;
                res += dfsnum(y);
            }
        }
        return res;
    }
	// dfs求连通块边的个数（总个数，最后还要 / 2）
    public int dfs(int x){
        int res = g[x].size();
        for(int y : g[x]){
            if(!vis[y]){
                vis[y] = true;
                res += dfs(y);
            }
        }
        return res;
    }
}

简洁写法，在一个dfs中求边和求点

class Solution {
    List<Integer>[] g;
    boolean[] vis;
    int v, e;
    public int countCompleteComponents(int n, int[][] edges) {
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for(int[] e : edges){
            g[e[0]].add(e[1]);
            g[e[1]].add(e[0]);
        }
        int ans = 0;
        vis = new boolean[n];
        for(int i = 0; i < n; i++){
            if(!vis[i]){
                v = 0;
                e = 0;
                dfs(i);
                if(e == v * (v-1))
                    ans += 1;
            }
        }
        return ans;
    }

    public void dfs(int x){
        vis[x] = true;
        v++;
        e += g[x].size();
        for(int y : g[x]){
            if(!vis[y])
                dfs(y);
        }
    }
}

方法二：并查集

题解：https://leetcode.cn/u/coco-e1/

并查集维护顶点数和边数

class Solution {
    int[] parent, cnt, size;

    public int countCompleteComponents(int n, int[][] edges) {
        parent = new int[n];
        cnt = new int[n]; // 边个数
        size = new int[n]; // 节点个数
        Arrays.fill(size, 1);
        for (int i = 0; i < n; i++) parent[i] = i;
        for (int[] e : edges) union(e[0], e[1]);
        boolean[] vis = new boolean[n];
        int ans = 0;
        for (int i = 0; i < n; i++) {
            int px = find(i);
            if (!vis[px]) {
                vis[px] = true;
                int s = size[px];
                if (cnt[px] == s * (s - 1)) ans++;
            }
        }
        return ans;
    }

    int find(int x) {
        if (parent[x] == x) return x;
        return parent[x] = find(parent[x]);
    }

    void union(int x, int y) {
        int px = find(x), py = find(y);
        if (px != py) {
            parent[px] = py;
            cnt[py] += cnt[px] + 2;
            size[py] += size[px];
        } else cnt[px] += 2;
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/527641.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Android 调用TTS语音引擎过程及问题记录

Android 调用TTS语音引擎过程及问题记录

Android 调用TTS引擎过程及问题记录 前言 背景是需要在华为平板上部署一个能够进行相关中文语音提示的APP&#xff0c;华为系统为鸿蒙3.0&#xff0c;对应Android API 12. Android 调用TTS引擎 调用TTS引擎之前&#xff0c;首先要确认自己的设备中是否安装了相关的文本转语音…
阅读更多...
从《水浒传》看项目管理

从《水浒传》看项目管理

水浒传和项目管理&#xff0c;这两个看似毫不相关的话题&#xff0c;其实有着惊人的相似之处。你没听错&#xff0c;就是水浒传&#xff01;这个充满了江湖义气和刀光剑影的故事&#xff0c;竟然能给我们现代人提供一些关于项目管理的启示。别怀疑&#xff0c;跟我一起来看看吧…
阅读更多...
nginx liunx最新版本安装flask部署

nginx liunx最新版本安装flask部署

一、nginx安装 1.进入Nginx官网的资源下载页&#xff1a;http://nginx.org/en/download.html 2.下载nginx-1.22.1.tar.gz&#xff0c; 3解压&#xff1a; tar -zxvf nginx-1.22.1.tar.gz解压完成后会在当前目录下得到一个新的nginx文件夹 4.终端进入nginx文件夹目录&#x…
阅读更多...
C++ -- AVL树插入实现和测试

C++ -- AVL树插入实现和测试

文章目录 1. AVL树概念2. AVL树满足性质3. AVL节点结构4. 插入操作5. 检测6. 完整代码 1. AVL树概念 AVL树就是自平衡二叉查找树&#xff0c;为了解决二叉树退化为单链表&#xff0c;使得增删查改时间度为O(N)&#xff0c;这里采用控制平衡策略达到效率是O(logN)。 2. AVL树满足…
阅读更多...
Golang结构体入门

Golang结构体入门

目录 结构体基础 结构体示例 为结构体定义方法 组合结构体 嵌套结构体 指针结构体 匿名字段 面向对象 封装 继承 多态 结构体基础 1.结构体是值类型&#xff1a;在Go语言中&#xff0c;结构体是一种值类型&#xff0c;与数组和基本数据类型一样。当结构体被赋值给一…
阅读更多...
【MySQL】MySQL批量插入测试数据的几种方式

【MySQL】MySQL批量插入测试数据的几种方式

文章目录 前言一、表二、使用函数生成设置允许创建函数产生随机字符串产生随机数字 三、创建存储过程插入角色表插入用户表 四、执行存储过程小结五、使用 Navicat自带的数据生成 前言 在开发过程中我们不管是用来测试性能还是在生产环境中页面展示好看一点, 又或者学习验证某…
阅读更多...
企业为什么要数字化转型？

企业为什么要数字化转型？

数字化转型是使用数字技术从根本上改变企业运营方式并为客户创造价值的过程。企业进行数字化转型&#xff0c;常见因素包括&#xff1a; 提高效率&#xff1a;数字化转型可以简化流程并自动执行重复性任务&#xff0c;从而减少执行这些任务所需的时间和精力。可以节省成本并提高…
阅读更多...
网页三剑客之 Javascript

网页三剑客之 Javascript

JavaScript (简称 JS) 是世界上最流行的编程语言之一是一个脚本语言, 通过解释器运行主要在客户端(浏览器)上运行, 现在也可以基于 node.js 在服务器端运行 其实&#xff0c;语言都是触类旁通的&#xff0c;我们学过了C语言和JavaSE&#xff0c;那么学起其他任何语言都不难&a…
阅读更多...
CSS 中的常用属性(图文详解版)

CSS 中的常用属性(图文详解版)

CSS 中的常用属性 &#x1f50e;引入方式&#x1f50e;CSS 选择器&#x1f50e;字体&#x1f50e;文本&#x1f50e;背景&#x1f50e;圆角矩形&#x1f50e;元素的显示模式&#x1f50e;CSS 盒模型&#x1f50e;弹性布局&#x1f50e;结尾 CSS 中的属性有很多 本文列举了一些较…
阅读更多...
Spark大数据处理讲课笔记4.4 Spark SQL数据源 - JSON数据集

Spark大数据处理讲课笔记4.4 Spark SQL数据源 - JSON数据集

文章目录 零、本讲学习目标一、读取JSON文件概述二、读取JSON文件案例演示&#xff08;一&#xff09;创建JSON文件并上传到HDFS&#xff08;二&#xff09;读取JSON文件&#xff0c;创建临时表&#xff0c;进行关联查询1、读取user.json文件&#xff0c;创建临时表t_user2、读…
阅读更多...
Liunx下的进程信号

Liunx下的进程信号

文章目录 前言1.信号初识前置知识2.信号产生的方式1.键盘产生信号2.系统调用产生信号3.软件条件产生的信号4.硬件异常 3.信号的保存4.信号的处理1.用户态和内核态2.用户态和内核态的切换方式3.内核中信号的捕捉流程4.volatile关键字 前言 本文主要是对Liunx中进程信息进行讲解…
阅读更多...
Spark大数据处理讲课笔记4.5 Spark SQL数据源 - Hive表

Spark大数据处理讲课笔记4.5 Spark SQL数据源 - Hive表

文章目录 零、本讲学习目标一、Spark SQL支持读写Hive二、Spark配置hive-site.xml三、准备工作&#xff08;一&#xff09;启动Hive的metastore&#xff08;二&#xff09;启动Spark Shell 四、Spark读写Hive数据&#xff08;一&#xff09;导入SparkSession&#xff08;二&…
阅读更多...
Spark大数据处理讲课笔记4.8 Spark SQL典型案例

Spark大数据处理讲课笔记4.8 Spark SQL典型案例

文章目录 零、本讲学习目标一、使用Spark SQL实现词频统计&#xff08;一&#xff09;数据源 - words.txt&#xff08;二&#xff09;创建Maven项目&#xff08;三&#xff09;添加依赖和构建插件&#xff08;四&#xff09;修改源目录名称&#xff08;五&#xff09;创建日志属…
阅读更多...
Linux——线程2|线程控制

Linux——线程2|线程控制

什么是线程 在一个程序里的一个执行路线就叫做线程&#xff08;thread&#xff09;。更准确的定义是&#xff1a;线程是“一个进程内部的控制序列”。 一切进程至少都有一个执行线程 线程在进程内部运行&#xff0c;本质是在进程地址空间内运行 在Linux系统中&#xff0c;在CPU…
阅读更多...
基于Java+SpringBoot+vue+node.js的智能农场管理系统详细设计和实现

基于Java+SpringBoot+vue+node.js的智能农场管理系统详细设计和实现

基于JavaSpringBootvuenode.js的智能农场管理系统详细设计和实现 博主介绍&#xff1a;5年java开发经验&#xff0c;专注Java开发、定制、远程、指导等,csdn特邀作者、专注于Java技术领域 作者主页 超级帅帅吴 Java项目精品实战案例《500套》 欢迎点赞 收藏 ⭐留言 文末获取源码…
阅读更多...
报表设计器Stimulsoft 2023.2提供深色主题和 Monoline 图标包

报表设计器Stimulsoft 2023.2提供深色主题和 Monoline 图标包

Stimulsoft Reports 是一款报告编写器&#xff0c;主要用于在桌面和Web上从头开始创建任何复杂的报告。可以在大多数平台上轻松实现部署&#xff0c;如ASP.NET, WinForms, .NET Core, JavaScript, WPF, Angular, Blazor, PHP, Java等&#xff0c;在你的应用程序中嵌入报告设计器…
阅读更多...
【Vue】学习笔记-消息的订阅与发布

【Vue】学习笔记-消息的订阅与发布

消息的订阅与发布(基本不用) 消息订阅与发布(pubsub)消息订阅与发布是一种组件间的通信的方式&#xff0c;适用于任意组件间通信 消息订阅与发布 1.订阅消息∶消息名 2.发布消息︰消息内容 消息订阅与发布的工作流程&#xff1a; &#xff08;A是订阅者&#xff0c;B是发布…
阅读更多...
软件安全开发意识

软件安全开发意识

国务院印发的《“十四五”数字经济发展规划》中指出数字经济是继农业经济、工业经济之后的主要经济形态&#xff0c;是以数据资源为关键要素&#xff0c;以现代信息网络为主要载体&#xff0c;以信息通信技术融合应用、全要素数字化转型为重要推动力&#xff0c;促进公平与效率…
阅读更多...
MYSQL高可用配置（MHA）

MYSQL高可用配置（MHA）

1、什么是MHA MHA&#xff08;Master High Availability&#xff09;是一套优秀的MySQL高可用环境下故障切换和主从复制的软件。 MHA 的出现就是解决MySQL 单点的问题。 MySQL故障切换过程中&#xff0c;MHA能做到0-30秒内自动完成故障切换操作。 MHA能在故障切换的过程中最大…
阅读更多...
fastapi高性能异步框架，极速上手

fastapi高性能异步框架，极速上手

fastapi项目开发快速上手 简介 FastAPI 是一个用于构建 API 的现代、快速&#xff08;高性能&#xff09;的 web 框架&#xff0c;使用 Python 3.6 并基于标准的 Python 类型提示。 特性: 快速&#xff1a;可与 NodeJS 和 Go 比肩的极高性能&#xff08;归功于 Starlette 和…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023