一、题目
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素
从左到右升序排列。
每列的元素从上到下升序排列。
二、示例
2.1> 示例 1:

【输入】matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
【输出】true
2.2> 示例 2:

【输入】matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
【输出】false
提示:
- m ==
matrix.length - n ==
matrix[i].length 1<= n, m <=300-10^9<= matrix[i][j] <=10^9- 每行的所有元素从左到右升序排列
- 每列的所有元素从上到下升序排列
-10^9<= target <=10^9
三、解题思路
根据题目描述,我们需要在矩阵matrix中寻找一个目标值target,并且该matrix具有两个特性:
【特性1】每行的元素
从左到右升序排列。
【特性2】每列的元素从上到下升序排列。
那么我们可以比较明显得感知到这两个特性就会是我们解开这个题的关键所在了。那么我们以示例一的矩阵作为例子,如果我们以某一个边角作为出发点,那么我们会得出如下结论:
【左上角】从
左到右,升序排列;从上到下,升序排列;
【右上角】从右到左,降序排列;从上到下,升序排列;
【左下角】从左到右,升序排列;从下到上,降序排列;
【右上角】从右到左,降序排列;从下到上,降序排列;
具体情况,请见下图所示:

那么,通过上面我们的分析,可以发现左下角和右上角这两个出发点才是我们解题的关键,因为这两个点在水平方向移动和在垂直方向移动分别是递增或者递减的;那么我们就可以执行如下逻辑:
【如果当前格子的值 小于 target】那么就向
递增方向移动;
【如果当前格子的值 大于 target】那么就向递减方向移动;
【如果当前格子的值 等于 target】那么返回true;
【如果移动 越界 并且 不等于 target】那么返回false;
上面就是具体的解题思路了,那么下面我们以输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5为例,来看一下具体的处理逻辑。请见下图所示:

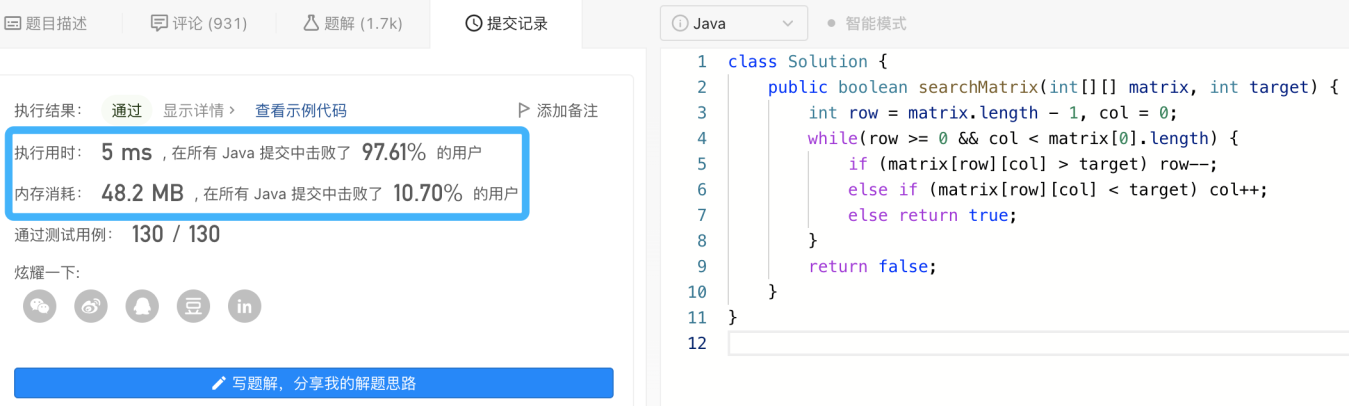
四、代码实现
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int row = matrix.length - 1, col = 0;
while(row >= 0 && col < matrix[0].length) {
if (matrix[row][col] > target) row--;
else if (matrix[row][col] < target) col++;
else return true;
}
return false;
}
}
今天的文章内容就这些了:
写作不易,笔者几个小时甚至数天完成的一篇文章,只愿换来您几秒钟的 点赞 & 分享 。
更多技术干货,欢迎大家关注公众号“爪哇缪斯” ~ \(^o^)/ ~ 「干货分享,每天更新」