一、图
1.图的概念
图是由顶点的有穷非空集合和顶点之间边的集合组成，通过表示为G(V,E)，其中，G标示一个图，V是图G中 顶点的集合，E是图G中 边的集合。
2.图的种类
图分为无向图和有向图
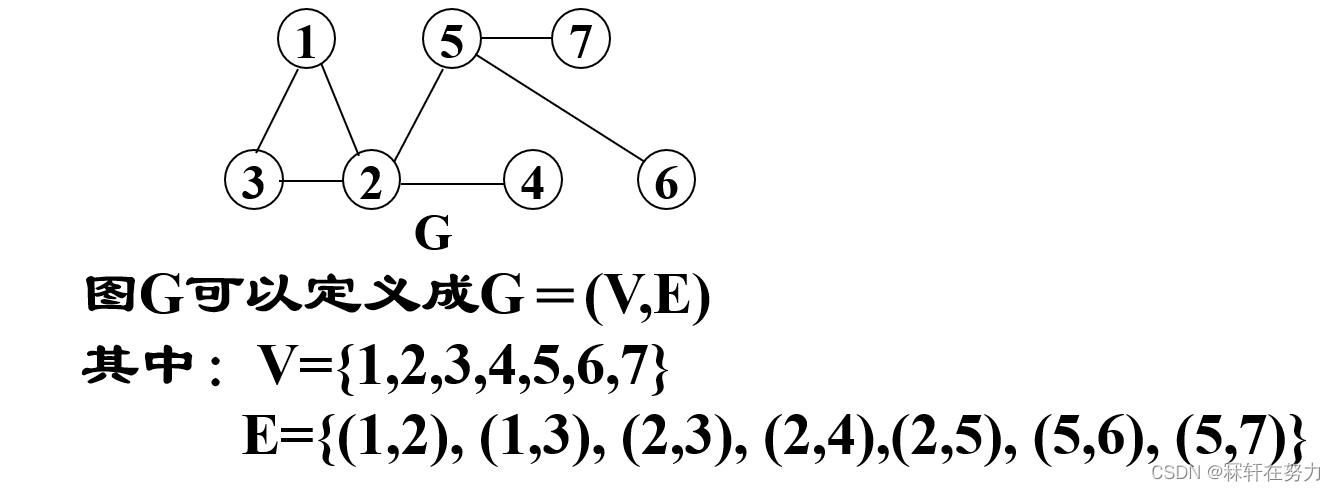
无向图：若顶点Vi到Vj之间的边没有方向，则称这条边为无向边（Edge），用序偶对(Vi,Vj)表示。
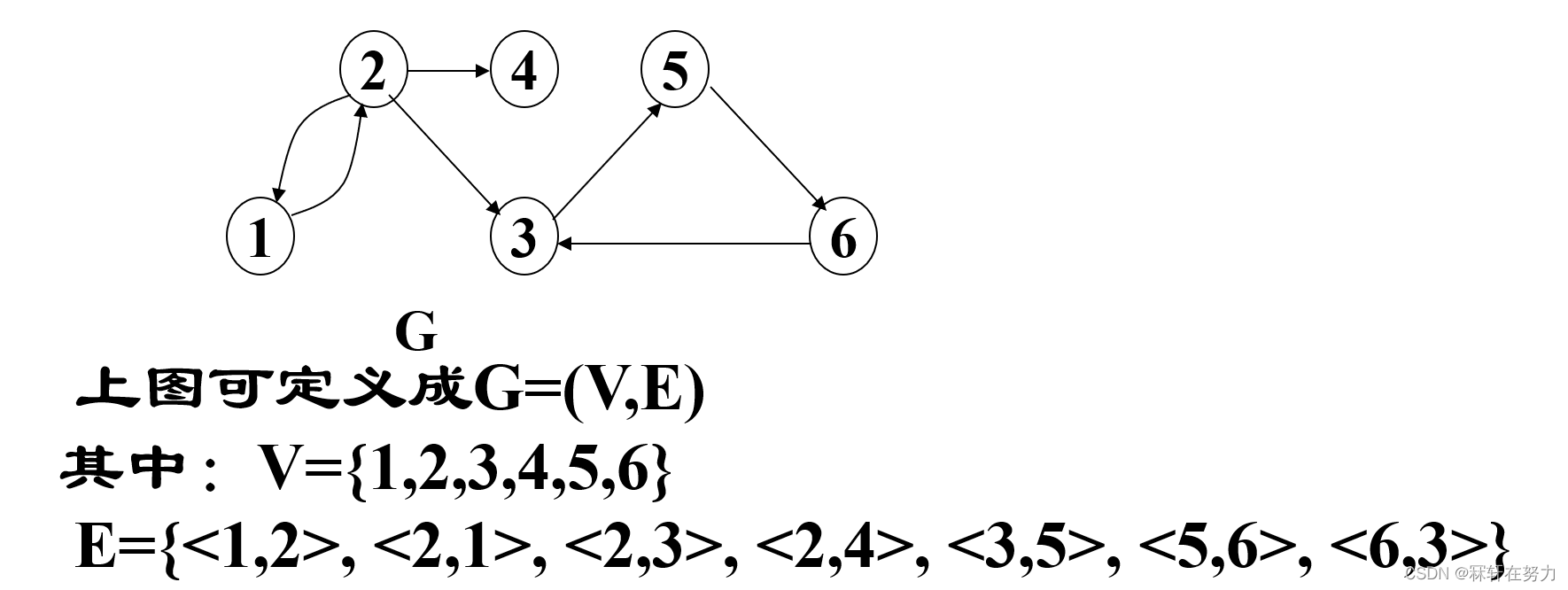
有向图：若从顶点Vi到Vj的边是有方向的，则成这条边为有向边，也称为弧（Arc）。用有序对（Vi，Vj）标示，Vi称为弧尾，Vj称为弧头。如果任意两条边之间都是有向的，则称该图为有向图。
无向图：
有向图：
二、图的创建（邻接矩阵）
用一维数组图中顶点的信息，用一个二维数组存储图中边的信息（各顶点之间的邻接关系）。存储顶点之间邻接关系的二维数组称为邻接矩阵。结点数为n的图G=(V,E)的邻接矩阵A是n*n的，将G的顶点编号为v1,v2,......vn。若（vi,vj)∈E，则A[i][j]=1，否则A[i][j]=0。
邻接矩阵用来存放边的，两顶点之间有边相连那么在邻接矩阵中它们对应的值为1，否则为0
就如A与B有边相连，那么它们对应的值就为一，A与A自身无边，那么就为零
1.邻接矩阵示意图
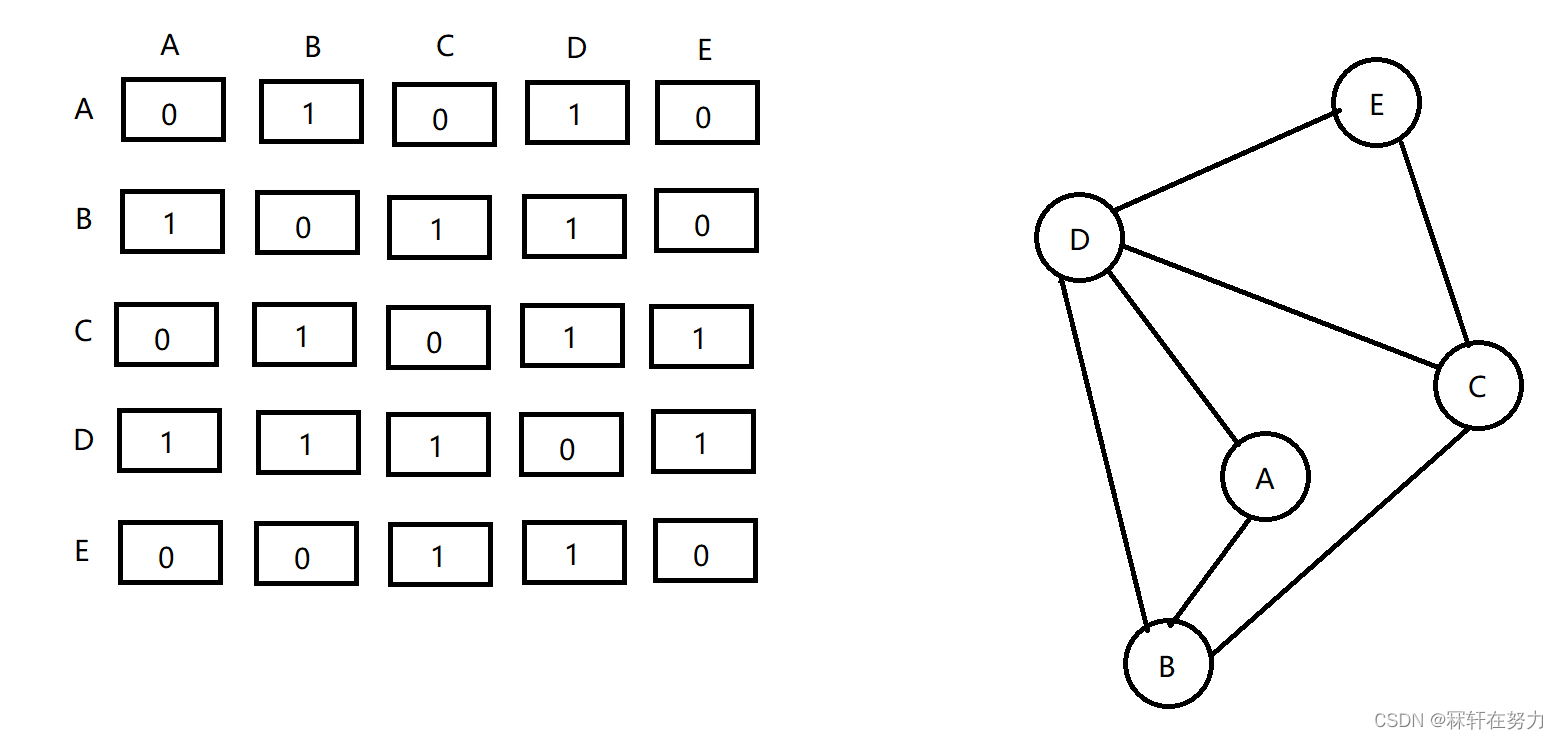
通过邻接矩阵得到的结论：
- 矩阵是对称的，可压缩存储（上（下） 三角）;
- 第i行或第i 列中1的个数为顶点i 的度;
- 矩阵中1的个数的一半为图中边的数目;
- 很容易判断顶点i 和顶点j之间是否有边相连(看矩阵中i行j列值是否为1)。
邻接矩阵法优点：
容易实现图的操作，如：求某顶点的度、判断顶点之间是否有边（弧）、找顶点的邻接点等。
邻接矩阵法缺点：
n个顶点需要n^2个单元存储边(弧);空间效率为O(n^2)。 适合于存储稠密图，对稀疏图而言浪费空间.
2.先创建图的结构体
typedef struct
{
char* vexs;//存放顶点的数组
int** arcs;//存放边的二维数组
int vexsnum;//顶点个数
int arcsnum;//边的数目
}graph;3.初始化图
首先申请相关数组的节点
graph* InitGraph(int vexsnum)
{
graph* g = new graph; //申请一个图结构体的节点
g->vexs = new char[vexsnum];//申请顶点个数大小的数组
g->arcs = new int* [vexsnum];//申请顶点个数大小的二维数组
for (int i = 0; i < vexsnum; ++i)
{
g->arcs[i] = new int [vexsnum]; //给二维数组中的元素申请一个数组
}
g->vexsnum = vexsnum;
g->arcsnum = 0;
return g;
}4.创建图
其中vexs表示顶点元素的数组，arcs表示存放边的二维数组
void CreateGraph(graph* g,char* vexs,int* arcs)
{
for (int i = 0; i < g->vexsnum; ++i)
{
g->vexs[i] = vexs[i]; //将顶点存入存放顶点的数组中
}
for ( int i = 0; i < g->vexsnum; ++i)
{
for (int j = 0; j < g->vexsnum; ++j)
{
g->arcs[i][j] = *(arcs+i*g->vexsnum+j);//将传入的二维数组赋值给图结构体中的二维数组
if (g->arcs[i][j] != 0)
{
++g->arcsnum;//判断边的个数
}
}
}
g->arcsnum /= 2;//得到有效边的个数
}g->arcs[i][j] = *(arcs+i*g->vexsnum+j);该语句是将arcs一维数组赋值给g->arcs二维数组
g->arcsnum /= 2;该语句除二的原因：
判断边的个数的时候，每个顶点都判断了一遍该顶点有几条边，所以重复判断了
需要除二来得到真实边的数目
三、深度优先遍历和广度优先遍历
3.1深度优先遍历主要思路：
从图中一个未访问的顶点 V 开始，沿着一条路一直走到底，然后从这条路尽头的节点回退到上一个节点，再从另一条路开始走到底…，不断递归重复此过程，直到所有的顶点都遍历完成，它的特点是不撞南墙不回头，先走完一条路，再换一条路继续走。
就如二叉树中的先序遍历一样，先访问根，左子树，再访问右子树
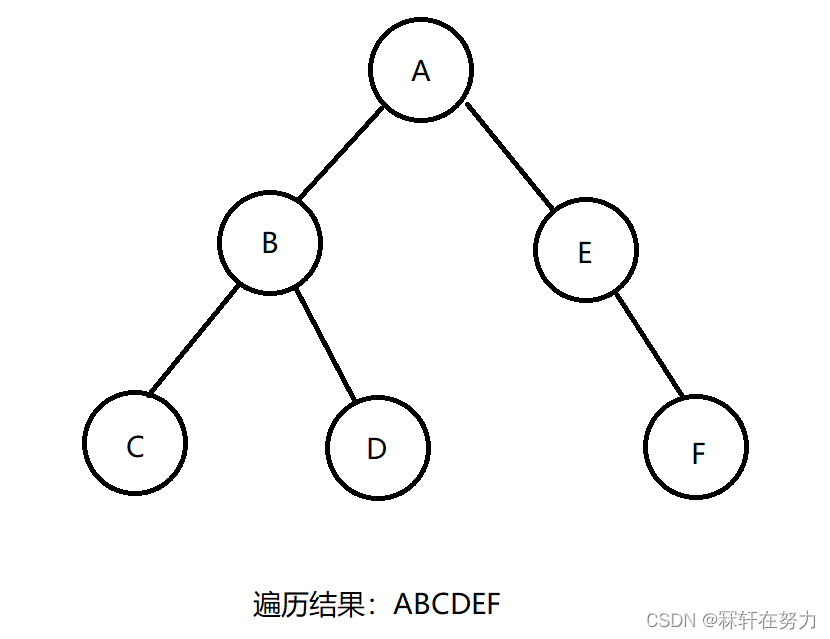
就像上面二叉树的先序访问一样，不撞南墙不回头
3.2图的深度优先遍历
visited表示一个一维数组，用来标记被访问过的节点
index表示从第几个顶点开始访问
void DFS(graph*g, int* visited, int index)
{
printf("%c ", g->vexs[index]);
visited[index] = 1;//标记已经被访问过的顶点
for (int i = 0; i < g->vexsnum; ++i)
{
//判断如果有边且该顶点没有被访问过，则可以访问
if (g->arcs[index][i] == 1 && !visited[i])
{
DFS(g, visited, i);//递归访问
}
}
}3.3广度优先遍历的主要思想：
从某个节点（源点）出发，一次性访问所有未被访问的邻接点，再依次从这些已访问过的邻接点出发，一层一层地访问。如下图所示，广度优先遍历是按照广度优先搜索的方式对图进行遍历的。
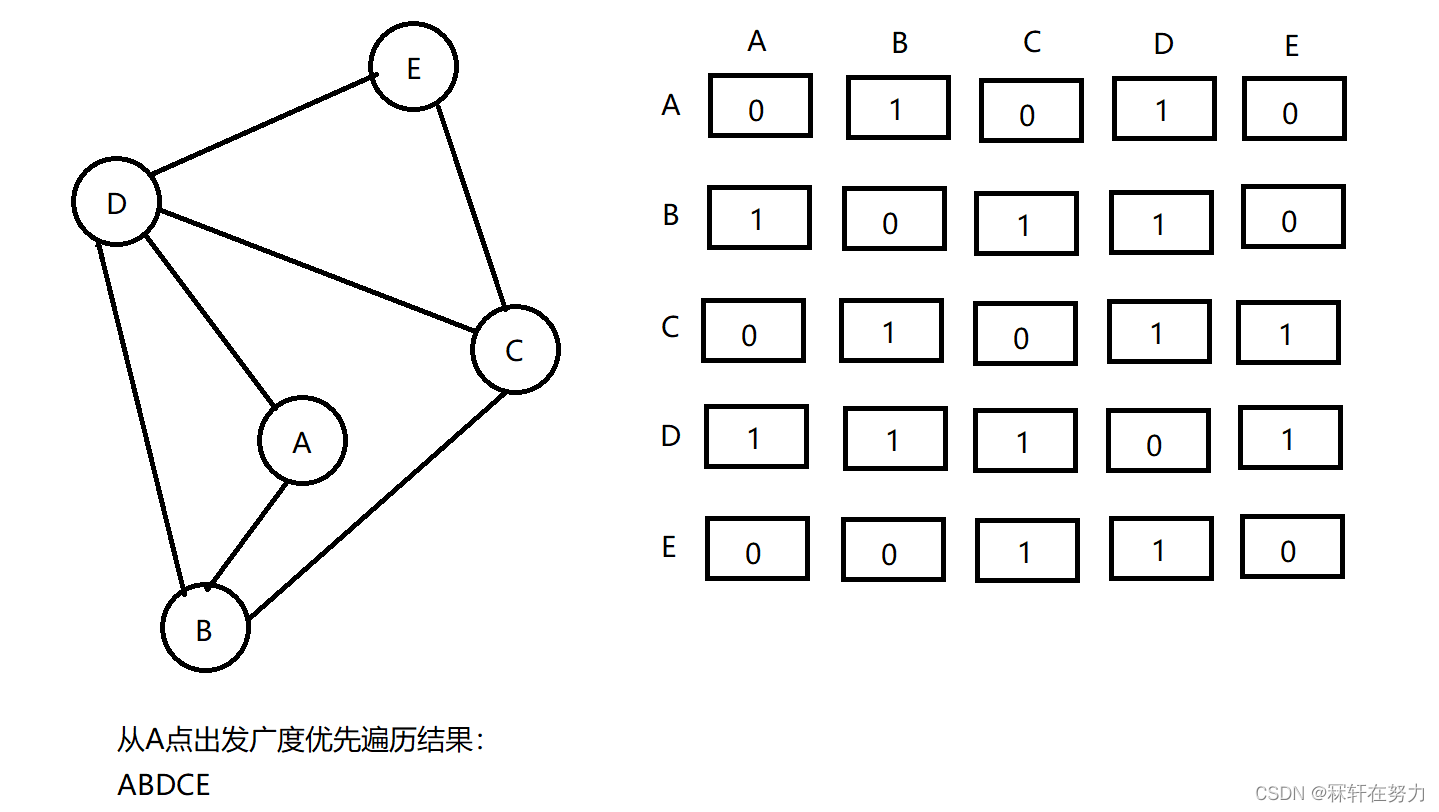通过观看右边的邻接矩阵，可以发现从A点出发，实际就是第一行先走完，然后再走B对应的那一行，再走D对应的那一行，再走C对应的那一行，最后走E对应的那一行
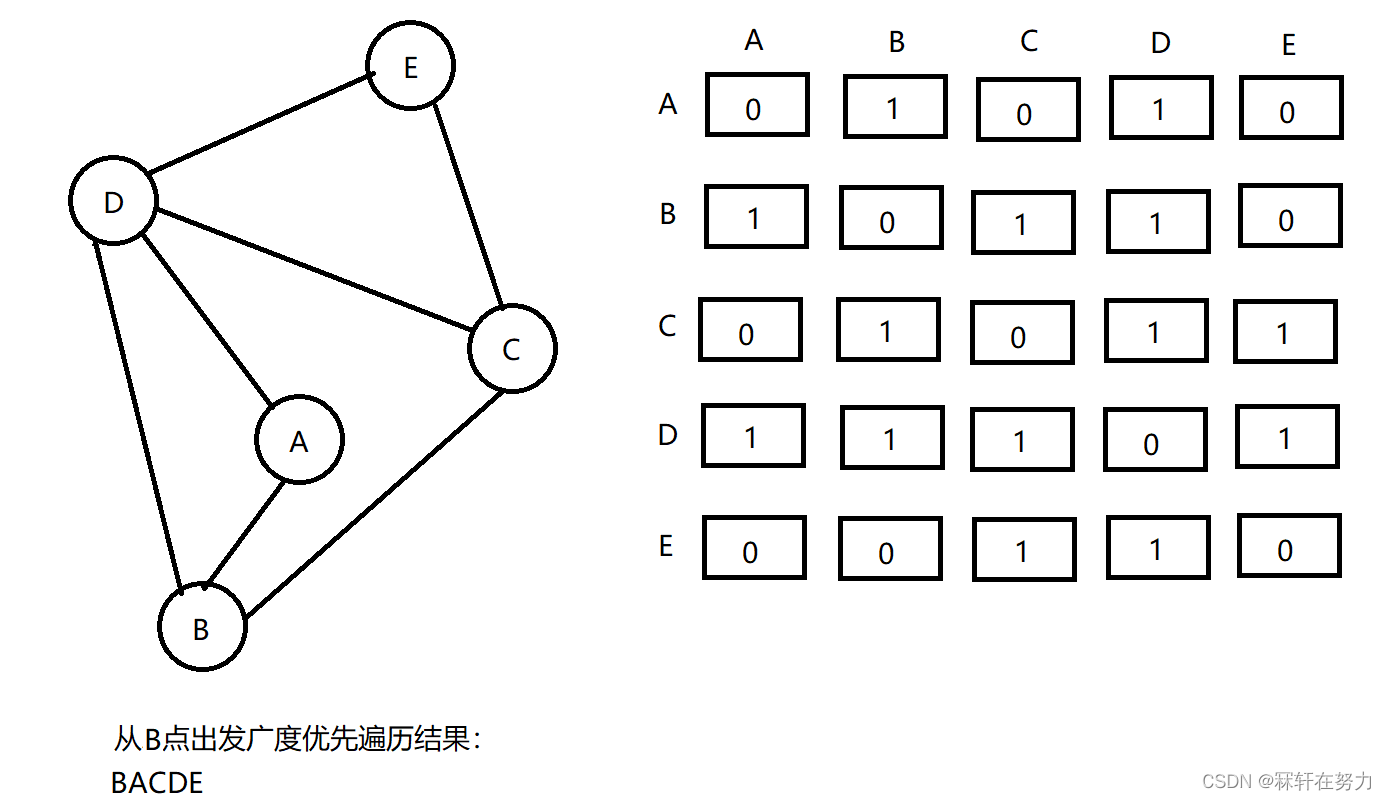
从B点出发，通过邻接矩阵可以发现，实际就是第B对应的那一行先走完，然后再走A对应的那一行，再走C对应的那一行，再走D对应的那一行，最后走E对应的那一行
3.4图的广度优先遍历
广度优先遍历就像二叉树中的层数，一层一层的走完。
通过上面的示例可以发现，图也是一层一层的走完，但是它不是按顺序走的，而是按先访问到谁就先走谁的那一行
有了这个思想，那么很显然此时我们就可以用队列来实现了，把访问到的顶点入队，然后等访问完 了该顶点相邻的顶点，就出队访问出队的顶点和其相邻的顶点，依次重复上述步骤，直到队列为空
void BFS(graph*g,int* visited, int index)
{
queue<int> q;
printf("%c ", g->vexs[index]);
visited[index] = 1;//标记
q.push(index);//入队
while (!q.empty())
{
int top = q.front();//出队
q.pop();
for (int i = 0; i < g->vexsnum; ++i)
{
if (g->arcs[top][i] == 1 && !visited[i])
{
printf("%c ", g->vexs[i]);
visited[i] = 1;
q.push(i);
}
}
}
}3.5图的实现代码
#include<iostream>
#include<queue>
using namespace std;
#define N 5 //N表示图的节点个数
typedef struct
{
char* vexs;
int** arcs;
int vexsnum;
int arcsnum;
}graph;
graph* InitGraph(int vexsnum)
{
graph* g = new graph; //申请一个图结构体的节点
g->vexs = new char[vexsnum];//申请顶点个数大小的数组
g->arcs = new int* [vexsnum];//申请顶点个数大小的二维数组
for (int i = 0; i < vexsnum; ++i)
{
g->arcs[i] = new int [vexsnum]; //给二维数组中的元素申请一个数组
}
g->vexsnum = vexsnum;
g->arcsnum = 0;
return g;
}
void CreateGraph(graph* g,char* vexs,int* arcs)
{
for (int i = 0; i < g->vexsnum; ++i)
{
g->vexs[i] = vexs[i]; //将顶点存入存放顶点的数组中
}
for ( int i = 0; i < g->vexsnum; ++i)
{
for (int j = 0; j < g->vexsnum; ++j)
{
g->arcs[i][j] = *(arcs+i*g->vexsnum+j);//将传入的二维数组赋值给图结构体中的二维数组
if (g->arcs[i][j] != 0)
{
++g->arcsnum;//判断边的个数
}
}
}
g->arcsnum /= 2;//得到有效边的个数，
}
void DFS(graph*g, int* visited, int index)
{
printf("%c ", g->vexs[index]);
visited[index] = 1;
for (int i = 0; i < g->vexsnum; ++i)
{
if (g->arcs[index][i] == 1 && !visited[i])
{
DFS(g, visited, i);
}
}
}
void BFS(graph*g,int* visited, int index)
{
queue<int> q;
printf("%c ", g->vexs[index]);
visited[index] = 1;//标记
q.push(index);//入队
while (!q.empty())
{
int top = q.front();//出队
q.pop();
for (int i = 0; i < g->vexsnum; ++i)
{
if (g->arcs[top][i] == 1 && !visited[i])
{
printf("%c ", g->vexs[i]);
visited[i] = 1;
q.push(i);
}
}
}
}
int main()
{
graph* g = InitGraph(N);//初始化图
char vexs[] = {'A','B','C','D','E'};//顶点元素
int visited[N] = { 0 };//用来标记的数组
int arcs[N][N] =
{
0,1,0,1,0,
1,0,1,1,0,
0,1,0,1,1,
1,1,1,0,1,
0,0,1,1,0
};//邻接矩阵
CreateGraph(g, vexs, (int*)arcs);//创建图
DFS(g, visited, 0);//深度优先遍历
printf("\n");
memset(visited, 0, sizeof(int) * N);//将标记数组重新置为0
BFS(g, visited, 1);//广度优先遍历
return 0;
}关于图的知识就分享到这了，谢谢支持！
