f
(
x
)
=
x
−
l
o
g
2
x
f(x)=\sqrt{x}-log_2 x
f(x)=x−log2x
对这函数求导后,比较分母大小,可以得到结论

f
(
x
)
f(x)
f(x)先减后增,分界点为
x
=
4
(
l
n
2
)
2
x = \frac{4}{(ln2)^2}
x=(ln2)24
f
(
x
)
f(x)
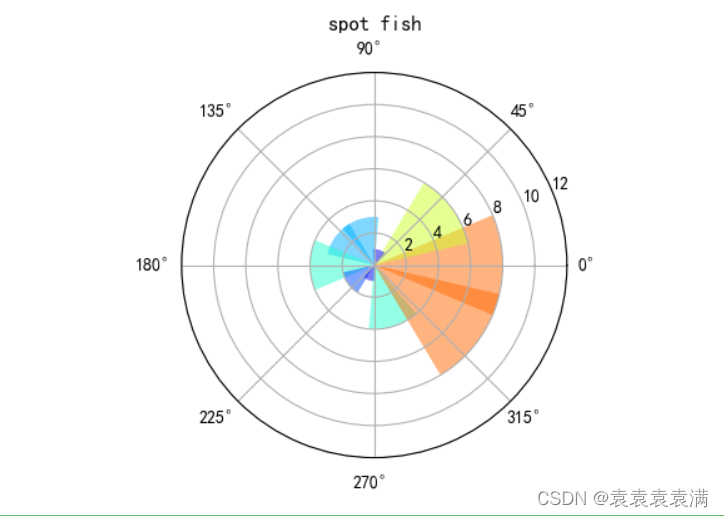
f(x)的图像如下所示:
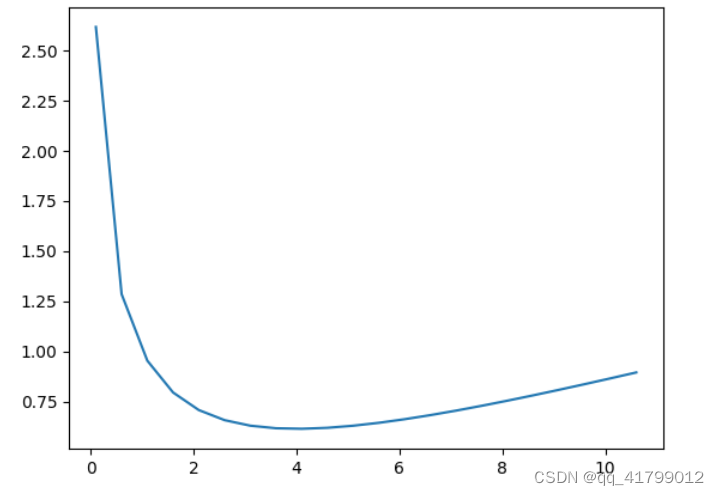
两个函数的图像如下,只在
x
=
4
,
16
x = 4,16
x=4,16时有交点

当n>16时,就必然
x
>
l
o
g
2
x
\sqrt{x}>log_2 x
x>log2x,故一般来说,
l
o
g
2
x
log_2 x
log2x更优
灵神题解的优越性,灵神题解










![[架构之路-199] - 可靠性需求与可靠性分析:鱼骨图、故障树分析法FTA、失效模式与影响DFMEA,找到影响故障的主要因素](https://img-blog.csdnimg.cn/img_convert/1fa4c3912a26a0152e477ee4a015cf69.jpeg)