2022 第十三届蓝桥杯大赛软件赛省赛(第二场),C/C++ 大学B组题解
文章目录
- 第1题 —— 练习 (5分)
- 第2题 —— 三角回文数 (5分)
- 第3题 —— 卡片 (10分)
- 第4题 —— 考勤刷卡 (10分)
- 第5题 —— 最大和 (15分)
- 第6题 —— 染色时间 (15分)
- 第7题 —— k 倍区间 (20分)
- 第8题 —— 选素数 (20分)
- 第9题 —— 第几小 (25分)
- 第10题 —— 单峰序列 (25分)
补题链接:地址

第1题 —— 练习 (5分)

- 题意:过了样例交上去0分,问可能是ABC的哪一种
- 显然都是,答案:ABC
#include <iostream>
using namespace std;
int main()
{
// 请在此输入您的代码
cout<<"ABC";
return 0;
}
第2题 —— 三角回文数 (5分)

-
题意:求第一个大于某2e8的数的回文数,且满足他可以等于1+2+…某个k。
-
一种是从2e8开始往上枚举,判断每个数是不是回文+三角,三角可以根号再乘附近的几个数特判一下。
另一种是枚举三角,1+2+…k,判断是不是回文和大于2e8,+k加到后面就是指数级了,上升也很快。 -
答案:35133153
#include<bits/stdc++.h>
using namespace std;
int main(){
int x = 0;
for(int i = 1; ; i++){
x += i;
if(x <= 20220514)continue;
string s = to_string(x);
string t = s;
reverse(t.begin(),t.end());
if(s==t)break;
}
cout<<x<<"\n";
return 0;
}
第3题 —— 卡片 (10分)

- 题意:n个人,给每个人随机发两张卡片(可以相同,没有顺序),求至少需要有多少种卡片,才能让n个人拿到的卡片组合都不同。
- 看一下样例,明显C(k,2)>=n,求k。(k-1)k/2>=n,可以跟上一题一样枚举,a[i]=a[i-1]+1递推上去即可。
#include<bits/stdc++.h>
using namespace std;
int main(){
int n; cin>>n;
int i, x = 0;
for(i = 1; ; i++){
x += i;
if(x < n)continue;
break;
}
cout<<i<<"\n";
return 0;
}
第4题 —— 考勤刷卡 (10分)


- 题意:n(1e4)条考勤记录,按顺序输出每个考勤了的员工的编号。
- 丢到set里输出就行,时间不用管。
#include<bits/stdc++.h>
using namespace std;
int main(){
int n; cin>>n;
set<int>se;
for(int i = 1; i <= n; i++){
string t; int id; cin>>t>>id;
se.insert(id);
}
for(auto x : se){
cout<<x<<"\n";
}
return 0;
}
第5题 —— 最大和 (15分)


- 题意:1-n共n个格子,每个格子有个分数(可能负数),开始站在1,下次可以跳到p+1到p+D(n-p)中的任意格子,D(x)为x的最小质因数,问能获得的最大分是多少。
- 数据范围n是1e4,感觉是个dp,状态到n为止能获得的最大分。 宝物绝对值不超过1e5,暴力转移的时候质因数分解logn(或者根号n直接暴力1e3最小质因数也可以的), nlogn刚好可以过。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
int a[maxn], f[maxn];
int isprime(int x){ //判断素数
for(int i = 2; i*i <= x; i++){
if(x%i==0)return 0;
}
return 1;
}
int find(int x){//找最小质因数
if(x==0 || x==1)return x;
for(int i = 2; i*i <= x; i++){
if(x%i==0 && isprime(i))return i;
}
}
int main(){
int n; cin>>n;
for(int i = 1; i <= n; i++)cin>>a[i];
memset(f, 0xc0, sizeof(f));
f[1] = a[1];
for(int i = 1; i <= n; i++){
int x = i+find(n-i); //最小质因数
for(int j = i+1; j <= x; j++){
f[j] = max(f[j], f[i]+a[j]);
}
}
cout<<f[n]<<"\n";
return 0;
}
第6题 —— 染色时间 (15分)


- 题意:给出nm的棋盘,初始都是白色,每个格子被染色后等aij秒变色,变色后对四周的格子都染色,每个格子只能被染色一次。时刻0对a00染色,求多少时间染完棋盘。
- 感觉暴力bfs遍历就行,加个堆每次取出当前最早变色的格子出来给周围的染一下,然后维护下每个格子有没有都被染过就行。数据范围500可以说是随便怎么写都行了。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 510;
int a[maxn][maxn], vis[maxn][maxn];
struct node{int x, y, time;}; //完成变色的时间
bool operator < (node a, node b){ return a.time > b.time; }
priority_queue<node, vector<node>, less<node> >q;
int dx[] = { 0,0,1,-1 };
int dy[] = { 1,-1,0,0 };
int main(){
int n, m; cin>>n>>m;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
cin>>a[i][j];
}
}
int res = 0;
q.push((node){1, 1, a[1][1]});
vis[0][0] = 1;
while(q.size()){
node t = q.top(); q.pop();
res = max(res, t.time);
for(int i = 0; i < 4; i++){
int nx = t.x+dx[i], ny = t.y+dy[i];
if(nx>=1&&nx<=n && ny>=1&&ny<=m && vis[nx][ny]==0){//没染过色
vis[nx][ny] = 1;
q.push((node){nx,ny, t.time+a[nx][ny]});
}
}
}
cout<<res<<"\n";
return 0;
}
第7题 —— k 倍区间 (20分)

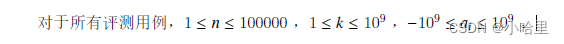
- 题意: 给出一个序列和一个k,求有多少个子区间的区间和是k的整数倍。
- 数据范围1e5,枚举所有区间是做不到了的, nlogn估计往数据结构去想,但是求子区间和无非也就是差分前缀和。
- 考虑前缀和求区间和,a[r]-a[l-1]是k的倍数,那么只要%k余数相同就好了,不难处理出过程中的前缀和值,然后前面有多少个跟当前%k余数相同的值,就是有多少个区间,扫一遍O(n)就行了(当然排序二分也是可以的,复杂度都一样,map查询logn,大家半斤八两)。
- 注意到一个坑点,不能是负整数倍,所以不能简单的累加,每次要遍历一遍%k余数的,要满足前面那个数比当前这个大才行。还有就是1e9的前缀和要开longlong。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
map<int,vector<LL>>mp; //mp[x]: 维护余数为x的前缀和有哪些
LL s[4]; //前缀和, 滚动数组
int main(){
int n, k; cin>>n>>k;
LL ans = 0;
mp[0].push_back(0); //别忘了
for(int i = 1; i <= n; i++){
int x; cin>>x;
s[i%2] = s[(i-1+2)%2]+x;
int r = (s[i%2]%k+k)%k; //%k余数
int len = mp[r].size();
for(int j = 0; j < len; j++){
if(mp[r][j] <= s[i%2])ans++;
}
// sort(mp[r].begin(), mp[r].end());
// ans += upper_bound(mp[r].begin(), mp[r].end(), s[i%2])-mp[r].begin();
mp[r].push_back(s[i%2]);
}
cout<<ans<<"\n";
return 0;
}
第8题 —— 选素数 (20分)

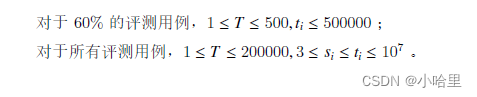
- 题意:给你两个数,s和t,每回合可以选一个小于s且不是s因数的素数p,然后找到p的倍数中刚好大于s的那个数y,并让s=y,进入下一回合。 求多少回合后s>t。
- 这题官网没有提交链接啊,代码补了对不对也不知道,我就不写了。。。(名正言顺的翘了摸鱼去了)
- 思路方向:
最大数据询问2e5,st 1e7,明显是个结论题, 可以找找规律。
20%的数据明显照着模拟就送。
50%数据500组,5e5,大概是优化下暴力,nlogn的复杂度,素数可以线性筛O(n)筛出来,个数大概是根号n,每次枚举每个素数,然后找倍数O1就够,如果满足条件就进入下一回合了,复杂度n根号n应该是可以拿到50%的。
或者,emmm,s-1,s-2这种很接近的数里应该有素数吧,并且肯定不是s的因数了,那么就O1过去了? 结论的话,盲猜跟gcd有点关系,不知道对不对,可以找找规律蛤。
第9题 —— 第几小 (25分)


- 题意:给一个数组,支持单点修改,以及求区间中比a[p]小的数的个数, a[p]在区间内。n是1e5,操作是2e5。
- 思路:首先,感觉暴力扫区间乱搞之类的可以拿40%。。1e5这种明显数据结构,区间操作就线段树。分块之类的应该也可以,一下子没想到线段树怎么维护,主席树第k小值应该可以做,感觉都有点长懒得写了,直接放一个可以过的分块代码
//分块可以AC 20个点的块长, sqrt(n)*5
#include<bits/stdc++.h>
using namespace std;
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int n; cin>>n;
vector<int> a(n+1,0);
//分块
int len = sqrt(n)*5; //块长
int k = (n%len==0)?n/len:n/len+1;//块数
vector<int> block[k+1]; //本体
vector<int> belong(n+1,0);
int blockNum = 0;
for(int i=1;i<=n;i++){ //分块
cin>>a[i];
blockNum=(i-1)/len+1;
belong[i]=blockNum;
block[blockNum].push_back(a[i]);
}
for(int i=1;i<=k;i++){ //块排序
sort(block[i].begin(),block[i].end(),less<int>());
}
//输入操作
int m; cin>>m;
vector<vector<int>> op(m,vector<int>(4,0));
for(int i=0;i<m;i++){
cin>>op[i][0];
cin>>op[i][1]>>op[i][2];
if(op[i][0]==2)cin>>op[i][3];
}
//执行
vector<int> res;
for(int i = 0; i < m; i++){
int num1=op[i][1], num2=op[i][2], num3=op[i][3];
if(op[i][0]==1){ //修改
auto it=lower_bound(block[belong[num1]].begin(),block[belong[num1]].end(),a[num1]);
block[belong[num1]].erase(it);
it=lower_bound(block[belong[num1]].begin(),block[belong[num1]].end(),num2);
if(it==block[belong[num1]].end())block[belong[num1]].push_back(num2);
else block[belong[num1]].insert(it,num2);
a[num1] = num2;
}else{ //查询
int count = 0, mid = a[num3];
//先查左右两端分块中满足条件的元组数,因为num1和num2所在的块不一定一整块都参与比较
for(int j=num1;j<=min(num2,belong[num1]*len);j++){
if(a[j]<mid)count++;
}
if(belong[num1]!=belong[num2]){
for(int j=(belong[num2]-1)*len+1;j<=num2;j++){
if(a[j]<mid)count++;
}
}
//区间查询,用二分法查询每个块中小于a[p]的元素个数
for(int j=belong[num1]+1;j<=belong[num2]-1;j++){
count+=lower_bound(block[j].begin(),block[j].end(),a[num3])-block[j].begin();
}
res.push_back(count+1);
}
}
for(auto &&num:res)cout<<num<<" ";
return 0;
}
第10题 —— 单峰序列 (25分)


- 题意:给出n和m,求构造序列满足长度1-n,和为m,且序列存在一个最高峰,左边递增右边递减,nm都是1e5,求可行的构造方案数。
- 显然是个dp,开始不难盲猜状态dp[i][j]为,长为i,总和为j的,满足xx条件的的个数,但是原先那个条件显然不太好转移, 考虑把条件改为严格递增,然后手动选取k点让严格递增的序列在k点左右两边自由组合,那么方案数就是排列组合2^x,可以算得出来。
- 转移就是长度i-1的加个数字过来,或者和为j-i的每个数加个1过来。因为需要包含最小元素1,所以先固定一个1,dp[i-1][j-1-(i-1)]=dp[i-1][j-i]。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL mod = 1e9+7;
LL pows(LL a, LL x, LL p){if(x==0)return 1; LL t = pows(a, x>>1,p);if(x%2==0)return t*t%p;return t*t%p*a%p;}
int main(){
int n, m; cin>>n>>m;
int nn = sqrt(2*m)+2;
while(nn*(nn+1)>2*m)nn--;
n = min(n, nn);
//dp
vector<vector<LL>>f(n+1, vector<LL>(m+1));
LL res = 1;
for(int i = 0; i <= m; i++)f[1][i] = 1;
for(int i = 2; i <= n; i++){
for(int j = 1; j <= m; j++){
if(i>=j)continue;
f[i][j] = (f[i][j-i]+f[i-1][j-i])%mod;
}
}
for(int i = 2; i <= n; i++){
res = (res+(f[i][m]*pows(2, i-1, mod))%mod)%mod;
}
cout<<res<<"\n";
return 0;
}