前言:与向量一样,矩阵也是3D数学的基础。要正确进行物体的位移、旋转和缩放变换,就必须要用到矩阵。
3D游戏中的向量一般只有3个维度,但矩阵要使用4×4矩阵,主要原因你是要用矩阵实现平移,3×3矩阵是不够的。4×4矩阵是能够进行所有常用变换的最小矩阵
常用矩阵介绍
由于矩阵算法的问题涉及面很广,本文只展示单独的平移、旋转和缩放矩阵,让小伙伴们对矩阵有一个直观的认识,消除陌生感
1.平移矩阵

向量v乘以上述向量 ,相当于让向量v的x、y、z分量分别变化为最后一行的xyz
2.旋转矩阵
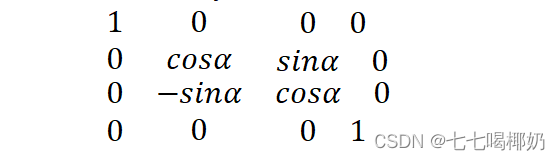
此矩阵可以让向量沿着x轴旋转α角
3.缩放矩阵
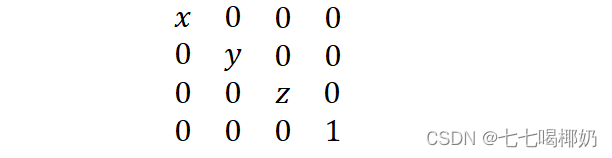
缩放矩阵可以对向量的各个分量进行缩放,向量v与上述矩阵相乘后,其三个分量分别缩放上图中的x、y、z倍
矩阵变换的最强大的地方在于,它可以通过矩阵乘法进行组合,组合以后通过一个矩阵就可以表示一组连续的变换操作。假设有3个矩阵S、R、T分别进行缩放、旋转、位移操作,三者相乘得到了M矩阵。那么有:vSRT=vM
虽然矩阵功能强大,但由于其使用有一定门槛,因此Unity封装了一些矩阵和变换矩阵,用户可以直接使用。旋转相关的问题还可以用四元数(Quaternion)来解决,进一步降低了直接操作矩阵的必要性
齐次坐标
在3D数学中,齐次坐标就是将原本的三维向量(x,y,z)用四维向量(x,y,z,w)来表示
引入齐次坐标有以下目的:
- 更好地区分坐标点和向量。在三维空间中,(x,y,z)既可以表示一个点,也可以表示一个向量。如果采用齐次坐标,则可以使用(x,y,z,1)代表坐标点,而用(x,y,z,0)代表向量。
- 统一用矩阵乘法表示平移、旋转和缩放变换。3×3矩阵可以用于表示旋转和缩放矩阵,但无法表示平移。用4×4矩阵就可以表示所有的常常用变换
- 齐次坐标是计算机图形学中的一个非常重要的概念,但在游戏逻辑开发中很少考虑齐次坐标的问题,只在处理渲染问题或编写着色器时会用到