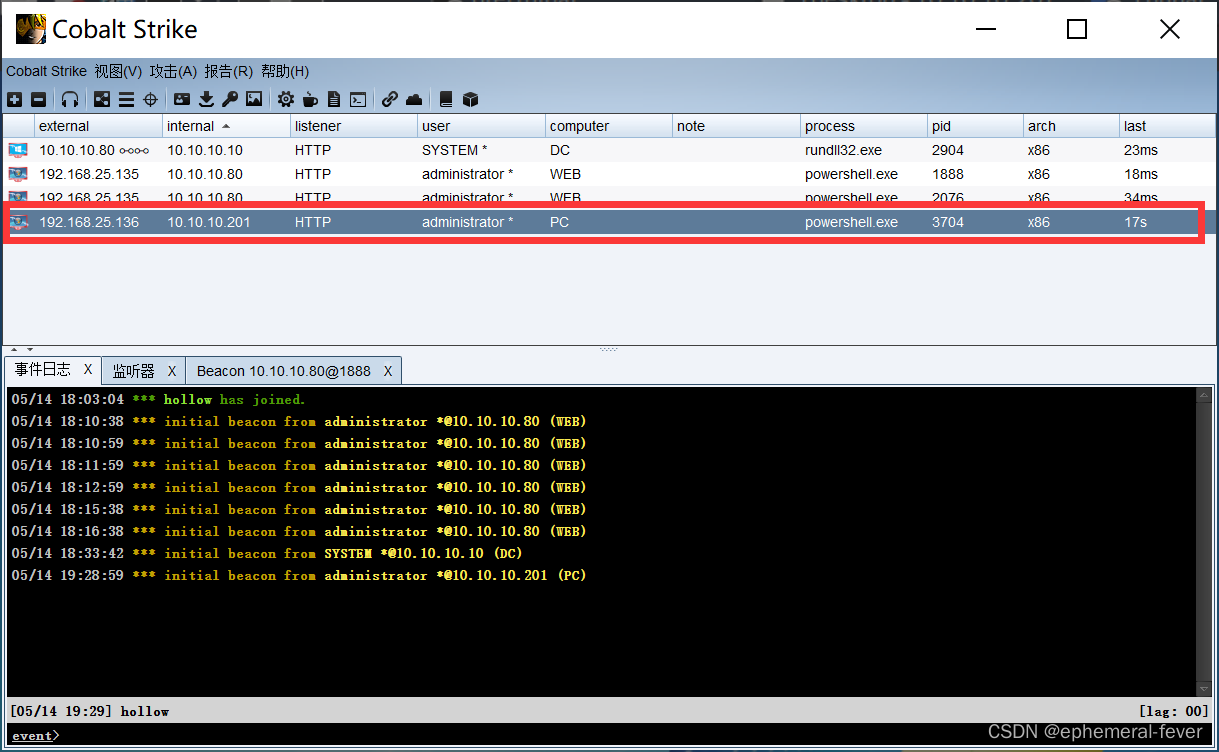
第 1 章学习Fourier分析的数学预备知识

1.1 引言

1.2 几何和代数的一些相关概念的回顾

1.2.1 标量运算(scalar arithmetic)

1.2.2 向量运算(vector arithmetic)

1.2.3 向量乘法(vector multiplication)

1.2.4 向量长度

1.2.5 本节小结

1.3 相量(phasors)和复数(complex numbers)的回顾

1.3.1 相量长度、复数大小和Euler公式

1.3.2 相量乘以复数(译注：相量也是复数)

1.3.3 复数的统计特性

1.4 术语总结

1.1 引言

为了培养对抽象概念的直觉理解，从不同的角度表达相同的思想常常能达到茅塞顿开的效果。Fourier分析可以从两个截然不同的有利角度(vantage)来看，一个是几何角度，另一个是分析角度。几何对视觉科学专业的学生有直接的吸引力，也许出于与它对古希腊几何学家的吸引力相同的原因。线条、形状和曲线的图形特性使几何成为数学中最直观的分支，也是最可感知的(tangible)分支。在另一方面，几何直觉很快导致一种情况，一位学生形象地将其描述为“精神便秘(mental constipation)”。 例如，在给定笛卡尔(Cartesian[ka:tí:ʒən])坐标(x,y)的情况下绘制一个点的想法很容易掌握，并且可以推广到 3 维空间，但许多学生很难超越物理世界的限制以想象在 4 维、5 维或 N 维空间中绘制一个点。在考虑用“穷竭法(method of exhaustion)” 求解圆的面积时，古希腊人的脑海中肯定也存在类似的困难。想法是在圆内刻上一个正多边形(regular polygon，规则多边形)，让边数从 3(三角形，a triangle)增加到 4(正方形，a square)等等，没有穷尽，如下图所示。

-----------------------------图 1.0 穷竭法求圆面积-----------------------------------------------------

但是他们从不相信多边形的面积会“准确地”匹配圆的面积,不管N增长到多大。另一个例子是Zeno[zí:nou]的二分法悖论(dichotomy paradox)：一支箭(arrow)要想射中目标，它必须先走完一半的距离，然后走完剩余距离的一半，等等。由于要穿越的一半距离有无数个，所以箭永远无法射中目标。这种概念上的障碍(hurdle)影响是如此之高，以至于直到 2000 年后的 17 世纪伟大的思想家才发明极限的概念，这是微积分的基础(Boyer，1949)，也是无穷级数 $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + .. = 1$ 的收敛性证明的基础。我的教学经验表明，我们中间仍然有很多古希腊人，他们通常首先在Fourier分析中试图从离散函数过渡到连续函数时表现出自己的古希腊人色彩。

当几何直觉失败时，分析推理可能会挽救危局。如果一个点在 3 维空间中的位置只是三个数字 (x，y，z ) 的列表，那么要在 4 维空间中定位一个点我们只需要扩展列表 (w， x，y，z )，无非是将字母表中的字母位置向前提一位！同样，我们可以分别通过用解析方程与其计算来代替几何对象及其操作来避开一些概念上理解的困难。出于这些原因，这些课程笔记(coursenotes)的前几章将采用双重思想呈现，一种是几何的，另一种是分析的。希望这种冗余方法将能帮助学生获得比单独使用任何一种方法所获得的理解更深入的理解。

现代学生可能会提出这样的问题：“既然我可以极易为我的个人计算机购买一个程序，只需按一下键它就能替我完成Fourier分析所能做的一切工作，那我为什么还要花时间学习Fourier分析呢？” 事实上，这似乎是一种普遍的态度，因为一个流行的分析程序的指导手册指出，“Fourier分析所做的事是每个人都在做的事情之一，但没有人理解其原理。” 这种态度在某些领域可能是可以容忍的，但在科学领域是不行的。实验者必须了解用于收集、处理和分析数据的任何工具的操作原理，这是一个基本原则。因此，本课程的主要目标是让学生了解Fourier分析——它是什么、它做什么以及它为什么有用。与任何工具一样，通过练习使用最容易理解，因此家庭作业问题构成了课程的一个组成部分。另一方面，这不是一门计算机编程课程，因此我们不会详细考虑使现代计算机程序如此高效优雅的快速傅里叶变换 (FFT) 算法。

研究Fourier分析还有另一个更普遍的原因。Richard[rítʃəd] Hamming[hǽmiŋ](译注：美国数学家)(1983) 提醒我们“计算的目的是洞悉(insight)，而不是为了数据结果！”。当直击问题使洞悉变得模糊时，改变视角通常会取得成功。Fourier分析是基于“变换(transformation)”思想改变视角的常规策略的一个典型例子。这个中心思想是在不同的领域，在新的背景下重铸问题，以便获得新的见解。Fourier变换将问题从时域或空间域转换到频域。事实证明，这样做具有巨大的实践裨益，因为在频域中，许多物理问题更容易理解，结果也更容易计算。这是Fourier分析对工程的一个主要吸引力：问题被转换到频域，进行计算，答案被转换回原始空间或时间域，以便在原始问题的背景下进行解释。上一代学生熟悉的另一个例子是取对数使乘法或除法更容易。因此，通过学习Fourier分析，学生将了解许多科学分支中使用的非常普遍的策略，以通过转换计算获得洞悉。

最后，我们研究Fourier分析，是因为它是描述自然界中周期性物理现象的天然工具。示例包括太阳季节的年度循环、月球事件的月度循环、昼夜节律的日度循环以及其他时间尺度为小时、分钟或秒的周期性事件，例如摆动的钟摆、振动的弦或电子振荡器。令人惊讶的事实是，用于描述周期性事件的工具也可用于描述非周期性事件。这种思想在Fourier时代引起了激烈的争论，但今天被认为是Fourier分析在现代科学中普遍适用的主要原因。

1.2 几何和代数的一些相关概念的回顾

1.2.1 标量运算(scalar arithmetic)

人类最早发明的数学思想之一是大小(magnitude)的概念。通过计数来确定大小显然是一个非常古老的概念，因为它在古代巴比伦(ancient Babylon)和古埃及(ancient Egypt)的记录中很明显。整数(whole numbers或integers)的概念在计数中是与生俱来的，整数的比率也被用来表示诸如1/2、3/4 等这样简单的分数。古希腊数学家将大小与线的长度或表面的面积相关联，因此开发了超越单纯计数的更进一步的计算方法。例如，可以通过使用图 1.1 中所示的圆规和直尺来实现大小的增加或减少。

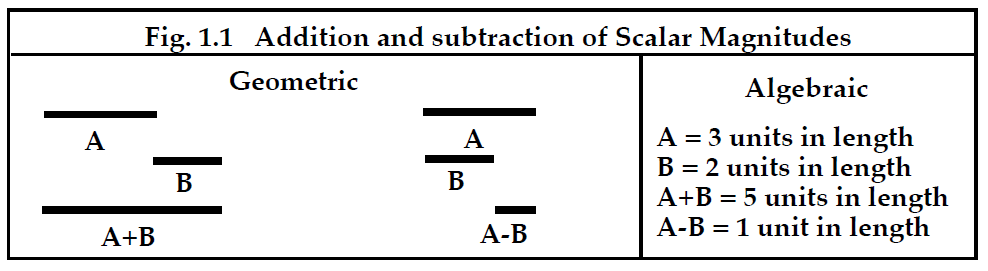
-----------------------------------------------图 1.1标题大小的加减法-------------------------------------------

如果线段 A 的长度表示要相加的一个量，而线段 B 的长度表示第二个量，则通过将两条线段首尾相连来机械地确定 A + B 之和。代数等价量是将一些合适的线段的长度定义为“单位长度(unit length)”。然后，借助圆规，计算标出 A 段和 B 段的整个长度所需的这些单位长度的整数。因此，总计数就是 A + B 段组合的长度。这种添加标量大小的方法是我们用等价几何和代数方法解决问题的第一个例子。

标量的减法也可以通过对齐 A 和 B 的左边缘以图形方式查看。A - B 的差值是从 A 中删除 B 后的余数。在这种几何构造中，B - A 的差值没有意义，因为 B 的长度不足以包含 A 。 处理这种情况促使阿拉伯数学家定义负数的概念，他们称之为“假(false)”或“虚构(fictitious)”，以承认对真实物体进行计数永远不会产生负数。另一方面，当你入不敷出时，负数就变成了会计学中一个非常真实的概念！

现在考虑确定两个大小之比的相关问题。显而易见的方法似乎是使用“单位长度”量尺求出两个大小的长度，并引用这些整数值的比值作为问题的答案。然而，这预示着总能找到合适的计量单位。可以想象，当古希腊数学家发现这个要求不能总是被满足时，对他们来说，这一定是一个毁灭性的打击。当试图确定正方形的边 ( A ) 和对角线 ( B ) 的长度比时，出现了一个明显的例子，如图 1.2 所示。

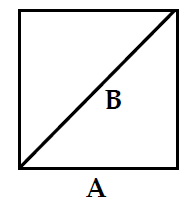
-----------------------------图 1.2 长度之比--------------------------------

线段 B 比线段 A 长，但是比 2 A 短。另一个例子是Pythagoras[paiθǽgəræs]黄金比例(Pythagoras’ Golden Ratio)： $( a + b ) / a = a / b = \phi = (1 + \sqrt{5} ) / 2$ 。古希腊人通过将长度 A 和 B 描述为“不相称(incommensurate)”来处理这种尴尬(akward)的情况。他们也可以使用“非比率(irrational)”、“不合逻辑(illogical)”、“错误(false)”或“虚构(fictitious)”等词来表达哲学上令人不安的(unsettling)认知，即某些比例不是整数的精确比率。

如今，我们对“非比数(irrational)”的概念感到满意，因为它们是不能“合法地”表示为两个整数之比的量(译注：即不能按分数表示成两个整数之比)。主流的例子是 $\sqrt{2}$ 、π、和 e 。然而，前面页中潜藏着类似的概念绊脚石，例如“负频率(negative frequency)”和“虚数(imaginary numbers)”，虽然一开始看起来不合逻辑且不合理，但通过熟悉使用，它们有望成为学生工具箱中值得信赖的工具。

1.2.2 向量运算(vector arithmetic)

一些物理量具有两个或多个需要量化的(quantified)属性。常见的例子是速率(velocity)，它是特定方向上的速度(speed)，以及力，它既有大小又有方向。这些量在几何上很容易可视化为称为向量(vectors)(译注：“向”指“方向”，“向量”即指有方向的量，又称“矢量”,在汉语中“矢”指的是“带有尖头的箭”,在不考虑阻力作用下，它射出去是朝着一个方向前进的，这里大概是引申为“方向”，实际上使用“矢”来表示方向在汉语词义中并不妥帖，谁是始作俑者如今已不得而知，但它已在各种译本中广泛散布开来，当我们见到“矢量”的时候，只要知道它就是“向量”就行了)的有向线段(图 1.3)。要创建向量的代数表示，我们可以简单地列出构成向量的两个标量大小，即(速度，方向)即可。这是向量记法的极坐标形式(polar form)。我们的物理经验提出了另一种表示，如果一个人以 3m/s 的速度北向行进，同时以 4 m/s 的速度东向行进，那么合成结果(net result)是在东北向上以 5 m/s 的速率(velocity)前进。因此，一个(二维)向量可以由一个列表指定，这个列表由两个正交(或垂直)(orthogonal)方向上的标量值组成。这种笛卡尔形式(Cartesian form)以传大的法国数学家René Descartes[rənéi，deiká:t]的名字命名，通常表述为“将一个原始向量分解为两个相互正交的分量”。

-----------------------------图 1.3 向量的描述------------------------------

现在考虑定义两个向量的加法或减法的含义的问题。我们的物理和几何直觉表明，加法的概念是笛卡尔表示向量的方法所固有的。也就是说，将东北向的速率向量 V 视为东向速率向量 X 和北向速率向量 Y 的总和是有意义的。在两个任意速率向量 A 和 B 的情况下，这种求和概念如何生效，是否不必正交？ 如果我们首先将这些向量中的每一个分解成它们的正交分量，就会出现一种简单的方法，如图 1.4 所示。由于东向的速度在向北方向的分量为零，我们可以简单地通过将两个向量的 X 分量相加来发现东向的合成速率。类似地，可以将两个 Y 分量加在一起以确定北向的总速率。因此，我们可以基于图 1.1 所示的标量加的直观概念，构建向量加的直观而令人满意的定义，这对于对诸如速率、力和正弦波形等物理量求和非常有用。向量差可以产生负值，这些负值在几何上由指左向或下向的向量表示。

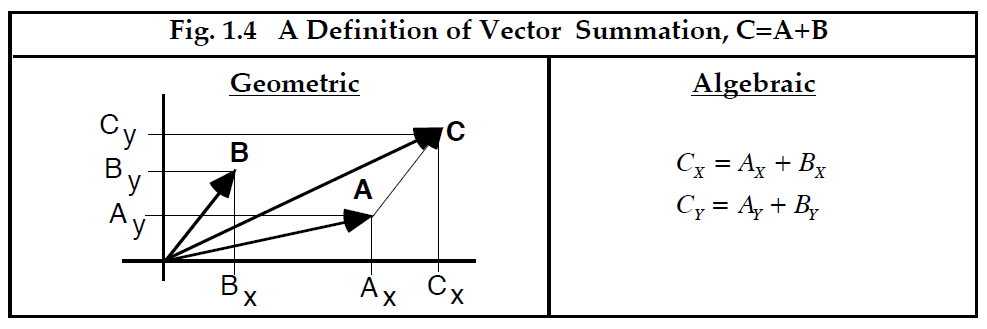
-----------------------------图 1.4 向量和的定义------------------------------

将二维向量的求和差代数表达式推广到3维向量只需要增加一个类似的方程 $C_{Z}$ 。然而，在纸上绘制 3 维几何图就已充满挑战性，要绘制更高维的向量几乎不可能做到。另一方面，将代数方法扩展到第 3、4 或第 N 维，就像向列表中添加另一个方程并定义一些新变量一样容易。因此，虽然几何方法更直观，但对于解决实际问题，代数方法通常是首选方法。

总而言之，我们发现，当向量应用于物理问题时，通过将向量分解为正交分量(orthogonal components)，再线性地组合向量(即，通过加法和减法)以产生合理的答案的简单规则就出现了。在Fourier分析中，我们遵循完全相同的策略来展示任意曲线如何可能地分解为正交函数(三角正弦函数和余弦函数)之和。按这种方式表示曲线，将出现用于组合曲线和计算物理事件输出结果的简单规则。

1.2.3 向量乘法(vector multiplication)

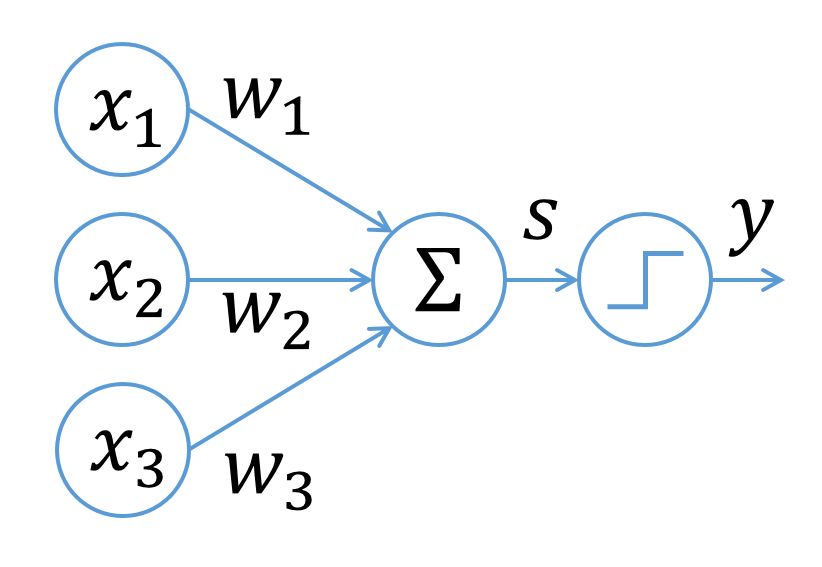
在小学阶段(elementary school)，孩子们学习的标量乘法可以理解为重复的加法运算。 然而，向量乘法是一个更丰富的主题，具有多种解释。Fourier分析最有用的定义反映了两个向量指向同一方向的程度(注：即，在多大程度上指出同一方向)。特别地，我们寻求当两个向量正交时乘积为零的定义。(可能认为零乘积条件应当保留给指向相反方向的向量，但这不是一个有趣的情况，因为相反的向量是共线的，因此退化为标量。在标量乘法中，实现零乘的唯一方法是被乘的标量之一为零。) 这表明，我们应当尝试这个规则：

A.B = (A的长度) × (B在A上的投影的长度)---------------------------[1.1]

注意，因为此规则求的是从原始向量导出的两个标量的乘积，所以结果将是一个标量(译注：也就是说，内积是标量积)。

[译注：

内积(inner product)(德语inneres produkt)这个术语由Hermann Günther Grassman (1809-1877) 于1844年在他的著作<<Die lineale Ausdehnungslehre>>(线性扩张论)中创造。

牛津词典第二版定义为"so named because an inner product of two vectors is zero unless one has a component 'within' the other, i.e. in its direction." (这样定义，是因为如果一个向量在另一个向量的"内部"有一个分量，即有一个分量与另一个向量在同一个方向，否则，两个向量的内积为0。) 根据这个定义，以二维向量为例，内积反应的是两个向量在多大程度上指向同一方向。如果完成垂直，即正交，那么其分量完全不在同一个方向上，所以内积为零。但为何不选择定义反向为内积0的条件呢？因为向量反向时，它们是花线的，因此，退化为标量了。

按Schwartzman：当德国梵文学者 Hermann Günther Grassman (1809-1877) 发展超复数的一般代数时，他意识到有可能存在不止一种类型的乘法。对于多种可能类型中的两种，他将其分别命名为内部的(inner)乘积和外部的(outer)乘积。选择这些名称似乎是因为它们是反义词而不是表示任何内在含义。

在英语中，内积(inner product)出现在 1909 年的韦伯斯特词典中，尽管 Cajori(1928-29)使用术语是内积(internal product)和外积(external product)。]

为了理解这个规则如何生效，我们考虑当向量 A 指向与 𝘟 轴相同的方向且两个向量之间的夹角为θ时的这种简单情况，如图1.5所示。接下来，将向量 B 分解为两个分别沿 𝘟 轴方向和 𝘠 轴方向的正交分量 ( $B_X , B_Y$ ) ，向量 B 的 𝘟 分量与向量 A 的方向相同，而向量 B 的 𝘟 分量的长度指的是“B 在A 上的投影的长度”。则我们可以利用三角公式推导出计算向量B 的 𝘟 分量长度的解析式 $B_{X}$ = |B|cos(θ)，其中，记法 |B| 表示向量B 的长度。注意，当θ = 90°时，内积(inner product)为0，据根需要，内积可能为负值，具体取决于从水平 (𝘟) 轴沿逆时针方向旋转的测度角θ 。

------------------------图 1.5 向量A.B的内积定义----------------------------

尽管假设向量 A 指向 𝘟 方向很方便，但图 1.5 的几何结构仍然适用于图 1.6 所示的通用情况。然而，如果能够计算两个向量的内积而不必首先计算向量的长度和它们之间夹角的余弦值，这将很有用。这可以通过使用三角恒等式来实现：

cos(θ) = cos(β - α) = cos(α )cos(β ) + sin(α ) sin (β )---------------- [1.2]

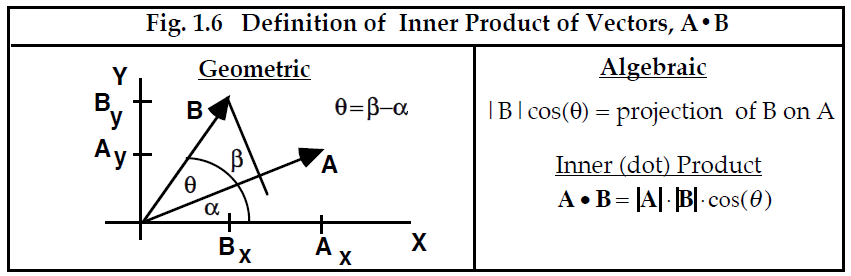
------------------------图 1.6 向量A.B的内积定义-----------------------------

假如我们将下面的关系代入等式[1.2]

$A_{X}$ = | A | cos(α )

$A_Y$ = | A | sin(α )

$B_X$ = | B | cos(β)

$B_Y$ = | B | sin(β) -----------------------------------------------[1.3]

则得到

$cos(\theta) = \frac{A_X B_X+A_Y B_Y}{| A || B |}-----------------------[1.4]$

这意味着

$| A || B | cos(\theta) = A_X B_X+A_Y B_Y ----------------[1.5]$

但是，等式的左边恰好是我们的向量A和B的内积的定义(见图1.5)。因此，我们得出了二维向量内积的最终公式

$A.B = A_X B_X+A_Y B_Y --------------------[1.6]$

换句话说，要计算两个向量的内积，只需简单地将向量的每个维度的正交分量的长度分别相乘，然后再将乘积结果相加。该公式很容易扩展到 N 维向量，且可以使用求和符号Σ 写成非常精简的形式，并可使用数字下标代替字母表示各个正交分量：

$A.B = A_1 B_1 + A_2 B_2 + A_3 B_3 + ... + A_N B_N$

$A.B = \sum_{k=1}^{N}A_k B_k --------------------- [1.7]$

1.2.4 向量长度

为了说明内积(“点积”)的有用性，考虑确定向量长度的问题。因为分量向量是正交的，所以适用毕达哥拉斯定理和直角三角形应用的几何学(图 1.7)。要开发相应的解析解，尝试组成向量与自身的内积。应用等式 [1.6] 可得出毕达哥拉斯提供的相同答案。也就是说，向量与自身的内积等于向量长度的平方。此外，这种计算向量长度的方法很容易通过使用等式 [1.7] 推广到 N 维向量。

------------------------图 1.7 使用内积计算向量长度----------------------------

1.2.5 本节小结

我们已经找到了与我们的几何直觉一致的向量加法和乘法的简单代数公式。这是可行的，因为我们选择用正交分量表示向量，然后对这些更简单的量进行代数运算。在Fourier分析中使用了相同的思想，我们将用正交函数(orthogonal functions)表示曲线。

1.3 相量(phasors)和复数(complex numbers)的回顾

看到用代数方式表达几何关系的一些优势之后，我们可能会更进一步，尝试发展正交几何概念的代数方面。要持有的关键思想是正交向量是彼此分开的且相互独立的，这使得正交分量可以单独相加或相乘。为了捕捉这种独立性的思想，我们可以尝试将不同的单位分配给不同维度的大小。例如，沿 𝘟 轴的距离可以指定为“苹果”单位，沿 𝘠 轴的距离可以称为“橙子”(图 1.8)。由于不能指望将苹果和橙子相加，因此该方案将在代数上强制实现在正交向量的几何中自然发生的这种类型的独立性和分离性。例如，令向量 P 的 𝘟 和 𝘠 分量分别具有长度 $P_{apples}$ 和 $P_{oranges}$ 且令 Q 的 𝘟 和 𝘠 分量分别具有长度 $Q_{apples}$ 和 $Q_{oringes}$ 。则和 S = P + Q 可以毫无歧义地解释为——向量S 的 𝘟 和 𝘠 分量分别具有长度 $P_{apples} + Q_{apples}$ 和 $P_{oranges} + Q_{oranges}$ 。

--------------------------------图 1.8 奇异的相量求和-----------------------------------------------

有一种更简单的方法，无需每次都编写两个相似方程即可保持向量分量代数独立性——将所有 𝘠 轴值乘以某个(目前暂未指定)称为“i”的量。现在我们可以将 P 写成 $P = P_X + iP_Y$ 而无需担心歧义解释，因为代数的基本法则阻止了等式右边两个不同类型项的求和。类似地，假如 $Q = Q_X + iQ_Y$ ，则我们可以使用基础代数确定和 $S = P + Q = P_X + Q_X iP_Y + iQ_Y = (P_X + Q_X ) + i (P_Y + Q_Y )$

，而无需担心搞混苹果和橙子。在工程学科中，以这种方式编写的二维向量通常称为“相量(phasors)”。

1.3.1 相量长度、复数大小和Euler公式

将 “i” 附加到沿 𝘠 轴的所有值的代数技巧提出了一种以代数方式计算相量长度的方法，该方法与图 1.7 的Pythagoras定理一致。在这个过程中我们也会发现“i”的价值。考虑图 1.9 中所示的相量，它具有单位长度并且具有从水平方向沿逆时针测量的倾斜角度 θ 。则，𝘟 分量的长度是 cos(θ)而 𝘠 分量的长度是 sin(θ)。因此，应用Pythagoras定理就可以证明这个著名的三角恒等式 $cos^2 (\theta) + sin^2 (\theta)) = 1$ 。当 y 坐标乘以 i 的时候，我们可以如何计算出这个答案呢？作为首次尝试，我们可以试着用相量 cos(θ) + i sin(θ)自乘，看看会发生什么：

$(cos(\theta) + i sin(\theta))^2 = cos^2 (\theta) + 2 i sin(\theta)cos(\theta) + i^2 sin^2 (\theta) -----[1.8]$

显然，这样进行不下去，因为预期的答案是1 。然而，注意到，假如我们乘以的相量不是它自己，而是它的共轭(conjugate)(译注：实部相共虚部相反的相量形式，看起来善于x对称，即所谓的“轭”的形状)，则我们会得到正确的答案(也就是说，这种方法算出的答案和几何方法得出的答案是一致的),其中，向量的共轭通过改变其y分量的符号而构成。换句话说，假如 Q = QX + iQY ，则其共轭 Q* = QX - iQY 。则其乘积 Q Q* 为

$Q Q* = (cos(\theta) + i sin(\theta))( cos(\theta) - i sin(\theta)) = cos^2 (\theta) - i^2 sin^2 (\theta)---[1.9]$

如果我们假设 $i^2=-1$ ，则 Q Q* = 1 正是所求的答案，与几何方法和使用 Pythagoras定理定理所求的一致。有了这个理由，我们定义 $i^2=-1$ 并定义 Q 的大小为 | Q | = $\sqrt{QQ*}$ , 它可以几何上解释向量Q的长度。

------------------------------图 1.9 向量单位------------------------------------------------------

在这一点上，我们所处的情况与古希腊人发现“非比数(irrational numbers)”以处理不相称长度时所处的情况，以及与阿拉伯人在发明负的“虚构的数”以处理从小数中减去大数时所处的情况大致相同。由于任何实数的平方都是正数， $i^2=-1$ 的定义似乎是不可能的，所以 i 这个量一定是“虚构的或想象的(imaginary)”！简而言之，我们发明了一种全新的量，并随之发明了复数的概念，复数就是与我们的几何相量相关联的代数名称。因此，复数(complex numbers)是基本“实(real)”量与这些通过将实数乘以 $i=\sqrt{-1}$

所产生的新“虚构”量的总和。我们现在可以放下我们的小游戏(charade)，承认苹果是实的，橙子是虚构的，制作复杂的水果沙拉时两者都需要！

持怀疑态度的学生可能会对上面强加的两个定义看似随意的性质保持警惕，事实上，它们可以得出所需的答案。然而，这种辩护在数学中并不少见，数学毕竟是一项发明，而不是一门服从自然规律的物理科学。对数学创造性的唯一限制是定义和操作在内部是一致的，这是我们对复数的定义必须使得其在Fourier分析中有用所做的辩护。

认识到不同数学思想之间的联系是数学家头脑的创造性行为。可以想象一下著名的瑞士数学家Leonhard Euler认识到复数指数是几何Pythagoras定理与复数代数之间的联系时所经历的智力顿悟(intellectual epiphany)。这个联系是通过Euler对复数指数函数的定义建立的，

$e^{i\theta} = cos(\theta) + i sin(\theta)$

$e^{(i(-\theta))} = cos(-\theta) + i sin(-\theta) = cos(\theta) - isin(\theta)-----------[1.10]$

根据代数基本法则，假如i 和e 是表示数的变量，则恒有

$e^{i\theta} . e^{i(-\theta)} = e^0 = 1 --------------------------[1.11]$

Euler和Pythagoras定理之间的联系很容易通过从 [1.11] 开始并使用 [1.9]、[1.10] 进行代数替换来证明，且 $i^2=-1$ 的定义如下：

$e^{i\theta} . e^{i(-\theta)} = 1$

(cos(θ) + i sin(θ))( cos(-θ) + i sin(-θ)) = 1

$cos^2 (\theta) - i^2 sin^2 (\theta) = 1$

$cos^2 (\theta) + sin^2 (\theta) = 1$ -----------------------------------------------[1.12]

Euler将三角函数组合成复数指数函数的方法广泛用于Fourier分析，因为它提供了一种用单个函数表示波形的正弦和余弦分量的有效方法(译注：因为指数函数的计算比正弦函数和余弦函数的计算简单)。然而，在这样做时，需要正频率和负频率，这可能会让初学者感到困惑。在本书中，我们采取的教学方法是先通过使用基本三角函数来熟悉Fourier分析，这种方法进展得更慢，因为在采用复指数函数之前，频率始终为正数。

1.3.2 相量乘以复数(译注：相量也是复数)

将相量的平方长度解释为复数的平方提供了一种方法来解决将两个不同相量相乘的更一般的问题，如图 1.10 所示。受Euler将相量表示为复数指数的公式的启发，我们将相量 P 写为

$P = P_X + iP_Y$

= |P| cos(θ) + i|P| sin(θ)

= |P|( cos(θ) + i sin(θ))

$= |P|e^{i\theta}$ -------------------------------------------------------[1.13]

为相量 Q 写一个类似的表达式，并应用代数的基本法则，得出两个相量的乘积是一个新的相量，其大小等于两个向量大小的乘积，角度等于两个向量角度之和：

$P. Q = |P|e^{i\theta}. |Q|e^{i\varphi} = |P| |Q|e^{i(\theta+\varphi)}$ ----------------------------------[1.14]

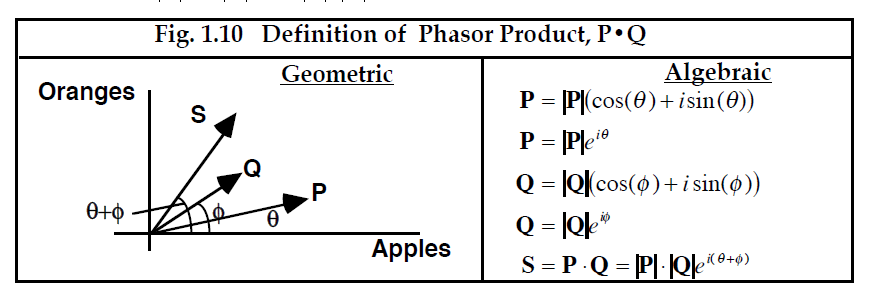
------------------------------图 1.10 相量积的定义-----------------------------

相量积的这个定义在概念上很简单，因为相量是用Euler的极坐标形式写的，带有大小和方向。但是，出于计算目的，可以将此定义重写为笛卡尔形式：

P = a + ib ；Q = c + id

$P Q = ac + iad + ibc + i^2bd$ ---------------------------------------------[1.15]

1.3.3 复数的统计特性

上面开发的复数相加规则允许我们将 N 个复数的平均值定义为总和除以 N。结果的实部是数字实部的平均值，结果的虚部是数的虚部的平均值。计算方差(variance)的第一步是从每个数中减去均值(mean)，这是通过从每个数的实部减去均值的实部以及从每个数的虚部减去均值的虚部来实现的。第二步是将数的平方和除以N。(统计学家区分总体的方差和从总体中抽取样本的方差。前者在分母中使用N，而后者使用N-1)。标准偏差只是方差的平方根。

------------------------------图 1.11 复数统计特性-----------------------------

1.4 术语总结

向量(vectors)在几何上被描述为具有特定长度和方向的有向线段。当向量投影到正交坐标轴上时，结果是一个有序的值列表。次序很重要！ [a,b,c] 与 [a,c,b] 是不同的向量。长度为 1 的向量称为单位标量(scalars)。所有维度都相同的向量集合，可以按行或按列分组到矩阵(matrices) 中。

相量(phasors)是二维向量的一种特例，其中 x 轴为实数，y 轴为虚数。作为实数和虚数之和的相量的代数表示称为复数。用于以图形方式描述相量的几何空间称为复平面(complex plane)。[译注：这里的“相”并不是方向的意思，“相”在汉语中的词义为“视，可视”的意思；而英语中“phase”的词义原本是“to show, to make appear”(显示，使可见),后来指“phase of the moon, particular recurrent appearance presented by the moon (or Mercury or Venus) at a particular time”)( 月相，月亮(或水星或金星)在特定时间呈现的特定反复出现的现象)，这种现象具有周期性；在物理学中，“phase”指物理变化中的某个状态，这种状态可以因某个量变化，表示这种因变的量称为“phase”,即某个状态“可视”时的“量”，称为“相量”，而确定其某个时刻位置的这个量称为“相位”；将正弦量(或余弦量)的大小和相位结合起来的这个二维向量称为相量。]

内容来源：

<< Fourier Analysis for Beginners>> Larry N. Thibos