文章目录
- 基本概念
- 平衡二叉树插入结点
- LL(左单旋)
- RR(右单旋)
- LR(左右旋)
- RL(右左旋)
- 示例插入推导过程
基本概念
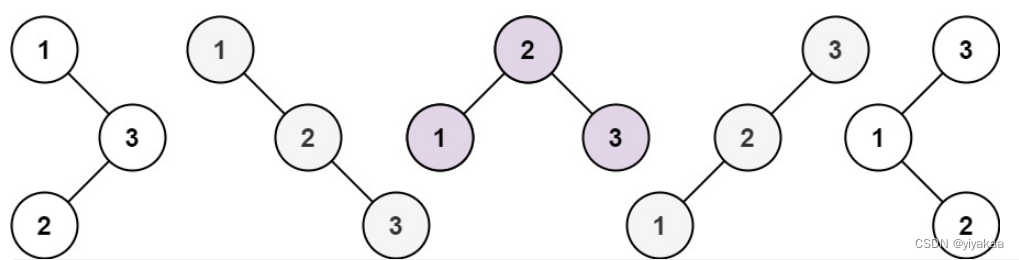
平衡二叉树是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树
又被称为AVL(Adelson-Velsky and Landis)树
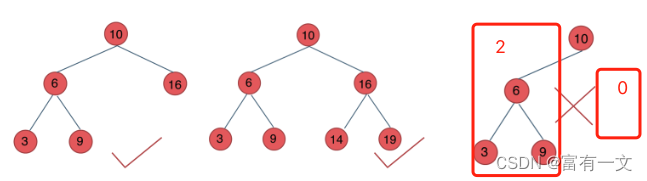
如图所示,第三个图中的树左右高差为2,是一颗不平衡的二叉树。
平衡二叉树插入结点
在平衡二叉树结点的插入过程中,可能会导致树从平衡变成不平衡的情况,具体有四种情况,如下所示:
LL(左单旋)

由于插入到左孩子的左孩子上导致的不平衡。
恢复平衡办法: 一次向右旋转即可
如图:以B节点为轴,向右旋转
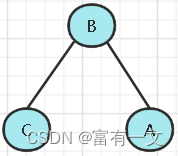
以B节点为轴向右旋转,B节点的右子树成为A节点的左子树
RR(右单旋)
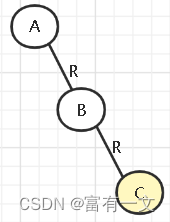
由于插入到右孩子的右孩子上导致的不平衡。
恢复平衡办法: 一次向左旋转即可
如图:以B节点为轴,向左旋转


以B节点为轴,向左旋转,B结点的左子树成为A节点的右子树
LR(左右旋)
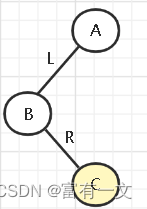
由于插入到左孩子的右孩子上导致的不平衡。
恢复平衡办法: 先向左旋转,再向右旋转
如图:
1、以B节点为轴,向左旋转
2、以C节点为轴,向右旋转


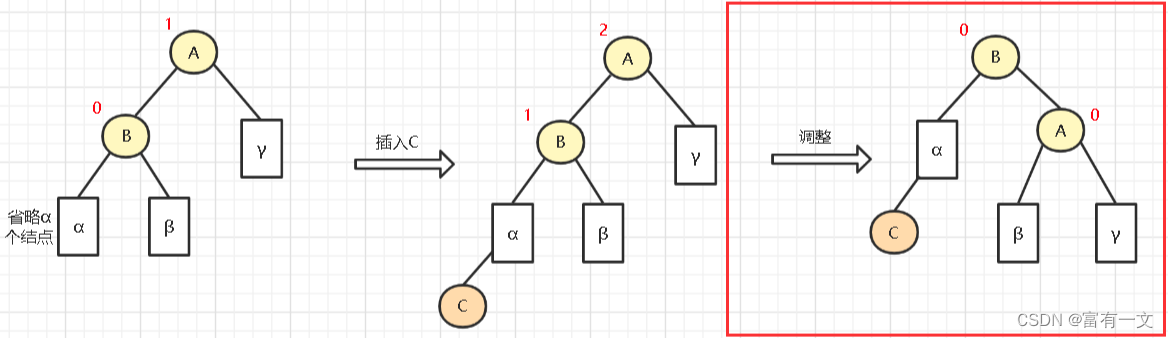
下图同上面图一个意思,只是考虑节点多一些。
RL(右左旋)

由于插入到右孩子的左孩子上导致的不平衡。
恢复平衡办法: 先向右旋转,再向左旋转
如图:
1、以B节点为轴,向右旋转
2、以C节点为轴,向左旋转

下图同上面图一个意思,只是考虑节点多一些。

示例插入推导过程
例题:输入关键字序列(16,3,7,11 ,9,26)给出AVL树
如图推导过程:
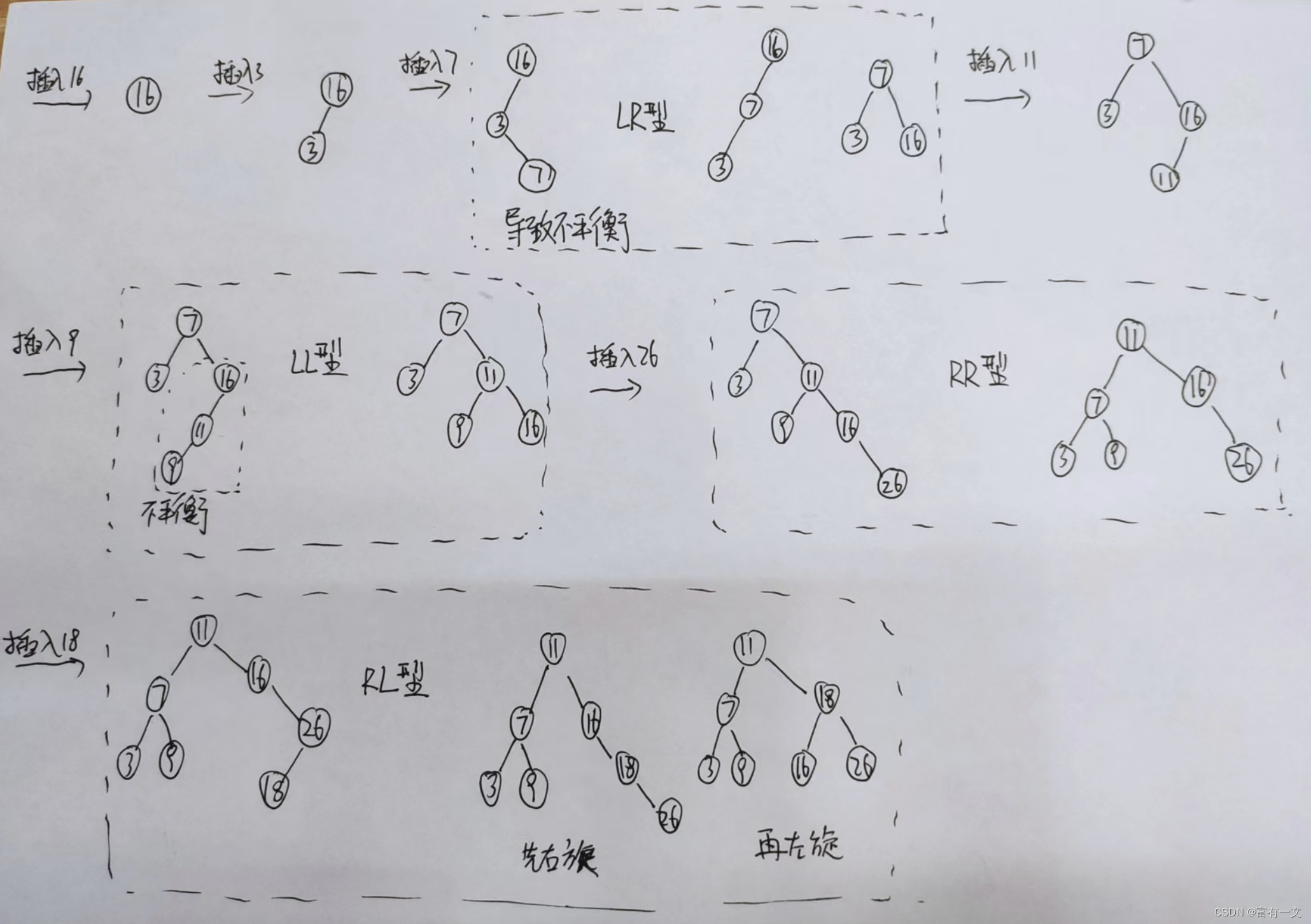
ps:计划每日更新一篇博客,今日2023-05-12,日更第二十六天。(补更)
昨日更新:
动态规划理论基础