题目： 给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

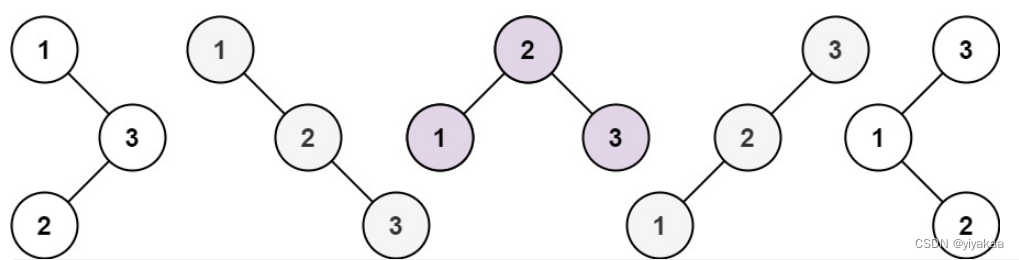
输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

思路：

1.确定dp数组的下标和含义
输入i得到dp[i]种不同的二叉树
2.递推公式
dp[i] += dp[j - 1] * dp[i - j]
3.dp数组初始化
dp[0] = 1;
4.遍历顺序
从小到大
5.打印
分析：当输入i为3时，可以分别用1，2，3作为头节点
当1作为头节点时，按照二叉搜索树的规则，其他两个节点只能在右边，并且只有两种情况
当2作为头结点时，按照二叉搜索树的规则，其他两个节点分别在两边
当3作为头节点时，按照二叉搜索树的规则，其他两个节点只能在左边，并且只能有两种情况
因此：
头1 = 左子树0节点*右子树2节点
头2 = 左子树1节点*右子树1节点
头3 = 左子树2节点*右子树0节点
dp[3] = dp[0]*dp[2]+dp[1]*dp[1]+dp[2]*dp[0]

class Solution {
public:
	int track(int n) {
		vector<int> dp(n + 1);
		dp[0] = 1;
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= i; j++) {
				dp[i] += dp[j - 1] * dp[i - j];
			}
		}
		return dp[n];
	}
};

int main() {
	int n = 3;
	Solution ss;
	cout << ss.track(n) << endl;
	return 0;
}