了解投影坐标系统，并在精美的地图上探索

news2025/11/4 3:15:40

投影坐标系简介

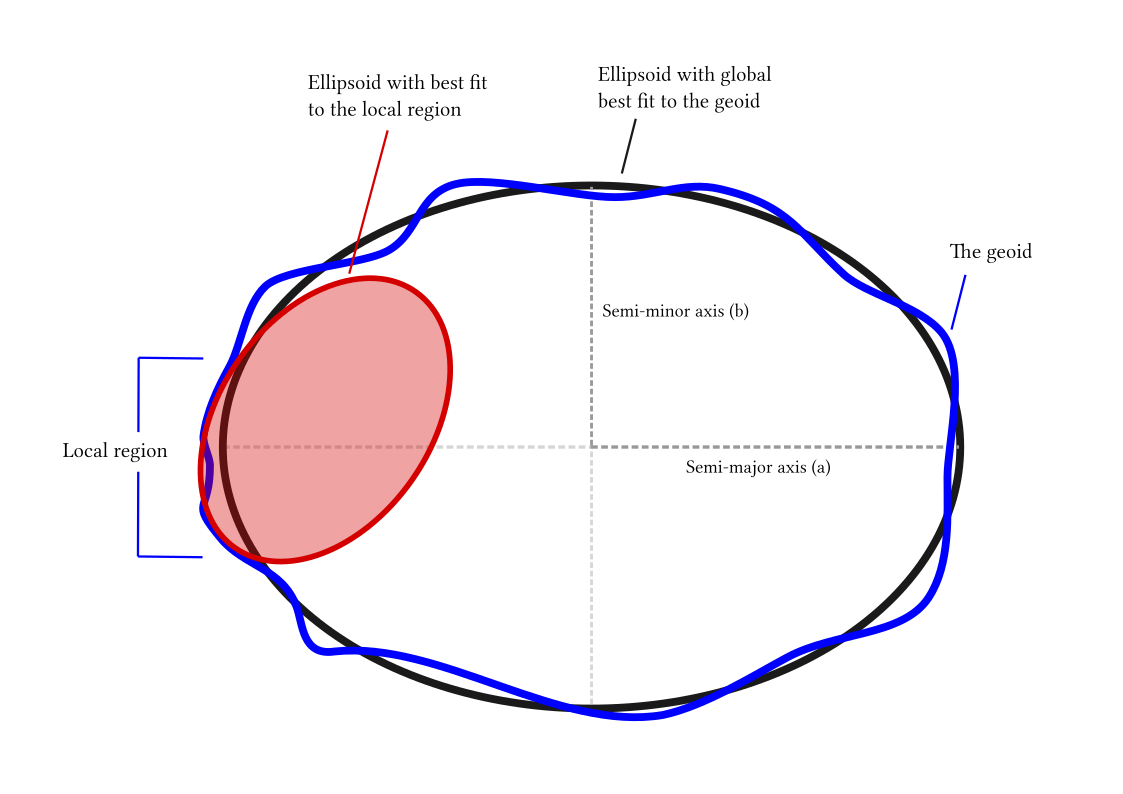
地球椭球体表面也是个曲面，而我们日常生活中的地图及量测空间通常是二维平面，因此在地图制图和线性量测时首先要考虑把曲面转化成平面。由于球面上任何一点的位置是用地理坐标（λ，φ）表示的，而平面上的点的位置是用直角坐标（X，Y）表示的，所以要想将地球表面上的点转移到平面上，必须采用一定的方法来确定地理坐标与平面直角坐标或极坐标之间的关系。这种在球面和平面之间建立点与点之间函数关系的数学方法，就是地图投影方法。
在这里插入图片描述

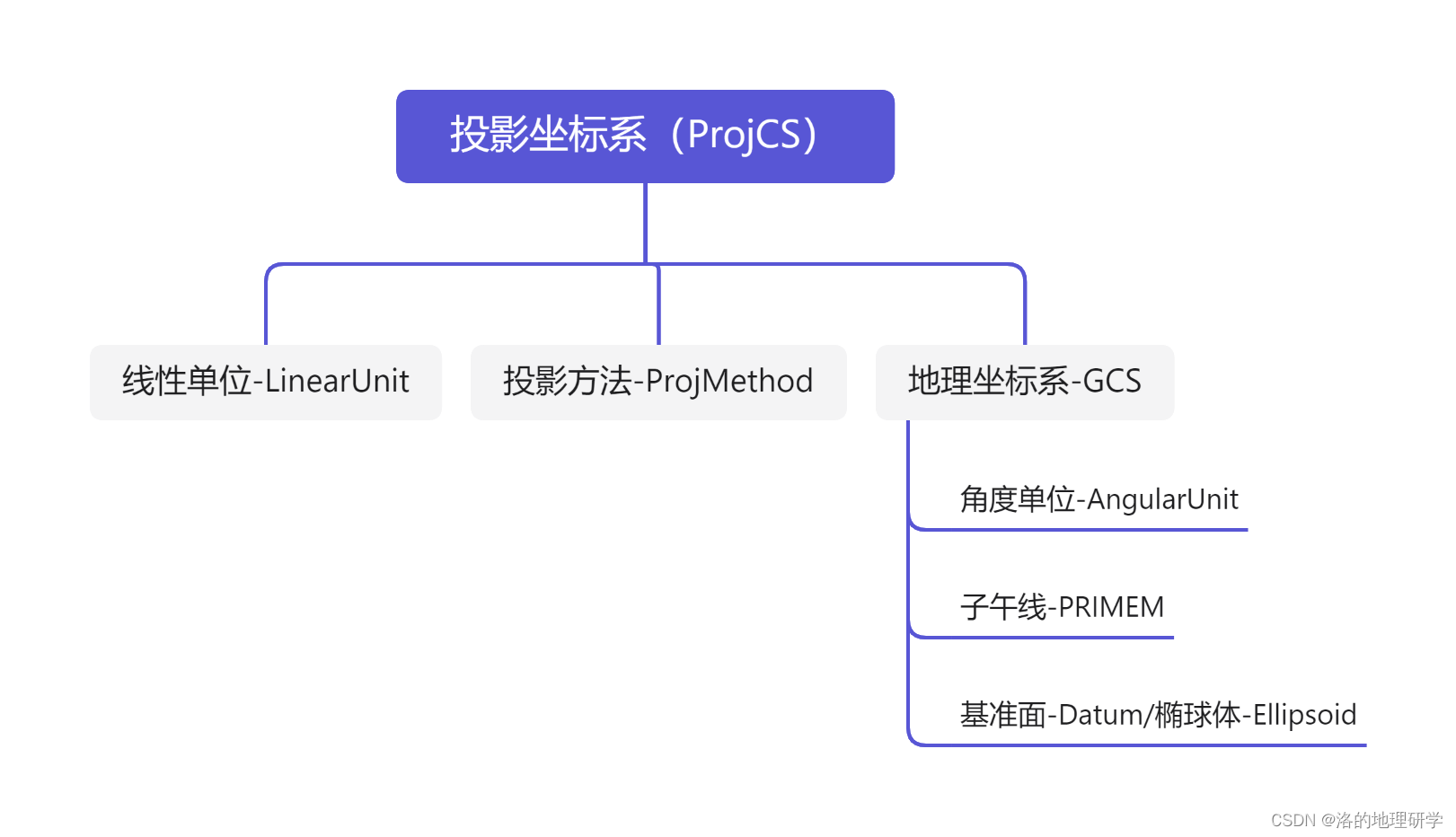
构成

投影坐标系使用基于 X，Y 值的坐标系统来描述地球上某个点所处的位置。这个坐标系是从地球的近似椭球体投影得到的，它对应于某个地理坐标系。投影坐标系主要由 地理坐标系、投影方法和线性单位 构成。
 　

线性单位

单位中文对照每单位长度（m）
metre米1
Clarke’s link克拉克令0.201166195164
Gold Coast foot黄金海岸英尺0.304799710181509
US survey foot美国测量英尺0.304800609601219
foot英尺0.3048
Clarke’s foot克拉克英尺0.3047972654
link令0.201168
British chain (Sears 1922 truncated)英国测链（1922年废弃）20.116756
Clarke’s yard克拉克码0.9143917962
kilometre千米1000
Indian yard印度码0.914398530744441
British chain (Benoit 1895 B)英国测链（贝诺伊特1895 B）20.1167824943759
British yard (Sears 1922)英国码（希尔斯 1922）0.914398414616029
German legal metre德国法定米1.0000135965
British chain (Sears 1922)英国测链（希尔斯 1922）20.1167651215526
British foot (Sears 1922)英国英尺（希尔斯 1922）0.304799471538676

投影方法

常用的投影长度单位如下：

投影方法中文对照
Transverse_Mercator横轴墨卡托投影
Oblique_Stereographic斜球面投影
Transverse_Mercator_South_Orientated横轴墨卡托投影（南向）
Hotine_Oblique_Mercator_Azimuth_Center洪特尼斜轴墨卡托方位角中心投影
Lambert_Conformal_Conic_1SP兰伯特等角圆锥投影（1 标准纬线）
Krovak克罗瓦克投影
Cassini_Soldner卡西尼-索尔德纳投影
Lambert_Conformal_Conic_2SP兰伯特等角圆锥投影（2 标准纬线）
Lambert_Azimuthal_Equal_Area兰伯特斜轴等面积投影
Lambert_Conic_Conformal_(West_Orientated)兰伯特圆锥等角投影（西向）
Mercator_1SP墨卡托投影（1 标准纬线）
Bonne_(South_Orientated)博恩投影（南向）
Albers_Conic_Equal_Area阿尔伯斯圆锥等面积投影（正轴等积割圆锥投影）
Polar_Stereographic_(variant_C)极球面投影（C 变体）
Polar_Stereographic极球面投影
Hotine_Oblique_Mercator洪特尼斜轴墨卡托投影
Hyperbolic Cassini-Soldner卡西尼-索尔德纳双曲线投影
Azimuthal_Equidistant等距离方位投影
Mercator_2SP墨卡托投影（2 标准纬线）
Cylindrical_Equal_Area圆柱等面积投影
Equirectangular球面投影
Guam Projection关岛投影
Krovak_Modified改良克洛瓦尔投影
Krovak_Modified_(North_Orientated)改良克洛瓦尔投影（北向）
Polyconic多圆锥投影
Lambert Conic Conformal (2SP Michigan)兰伯特圆锥等角投影（2 标准纬线，密歇根州）
Colombia Urban哥伦比亚城市投影
Tunisia_Mapping_Grid突尼斯地图网格投影
Lambert_Conic_Near-Conformal兰伯特圆锥近等角投影
New_Zealand_Map_Grid新西兰地图网格投影
Laborde_Oblique_Mercator拉伯德斜墨卡托投影
Lambert_Conformal_Conic_2SP_Belgium兰伯特等角圆锥投影（2 标准纬线，比利时）
Transverse_Mercator_Zoned_Grid_System横向墨卡托分区网格投影系统

地理坐标系

地理坐标系是使用三维球面来定义地球表面位置，以实现通过经纬度对地球表面点位引用的坐标系。一个地理坐标系包括 角度测量单位、本初子午线和参考椭球体/基准面 三部分。在球面系统中，水平线是等纬度线或纬线。垂直线是等经度线或经线。

常见的 WGS 84、CGCS 2000 等都属于地理坐标系。

gma 2 坐标参考系统简介

gma 简介

gma 是一个基于 Python 的地理、气象数据快速处理和数据分析函数包（Geographic and Meteorological Analysis，gma）。gma 1.x 网站：gma.luosgeo.com。

下文使用 gma 2 绘制 20 余种投影下的世界地图。

gma 的主要功能

气候气象（例如 SPEI、SPI、ET0 等）
遥感指数（例如 NDVI、EVI、TVDI 等）
数学运算（例如 数据平滑、评估、滤波、拉伸、增强变换等）
系统交互（例如 获取路径、重命名、压缩等操作）
空间杂项（例如 计算空间距离、面积计算，坐标转换、空间插值等操作）
栅格处理（例如 栅格镶嵌、裁剪、重采样、重投影、格式转换、数据融合等）
栅格分析（例如 DEM 坡度、坡向、阴影、等值线等计算）
矢量处理（例如 矢量裁剪、擦除、交集、融合、重投影等）
地图工具（例如 栅格、矢量数据绘图，指北针、比例尺等生成，坐标系定义等）

gma 2 下载

目前，gma 2 为前期测试版本，版本号 2.0.0a1，下载地址：

​链接：https://pan.baidu.com/s/17TGMjNi7ZU0Ln1KvcCtvqQ?pwd=tz0s
提取码：tz0s

坐标参考系统模块的主要功能

目前，gma 2 的坐标参考系统（gma.crs）提供：

1. 基准面（gma.crs.Datum）

创建一个基准面。

2. 椭球体（gma.crs.Ellipsoid）

创建一个椭球体。

3. 地理坐标系（gma.crs.GeogCS）

创建一个地理坐标系。

4. 投影坐标系（gma.crs.ProjCS）

创建一个投影坐标系。

5. 内置参数

椭球体（gma.crs.Ellips）

创建一个椭球体。也提供一些内置的椭球体，包括：

椭球体名称长半轴（m）反扁率
Airy18306377563.396299.325
AiryModified18496377340.189299.325
AustralianNationalSpheroid6378160298.25
AverageTerrestrialSystem19776378135298.257
Bessel18416377397.155299.1528
BesselModified6377492.018299.1528
BesselNamibia6377483.865299.1528
CGCS20006378137298.2572
Clarke18586378293.645294.2607
Clarke18666378206.4294.9787
Clarke18806378249.145293.4663
Clarke1880ARC6378249.145293.4663
Clarke1880Benoit6378300.789293.4663
Clarke1880ING6378249.2293.466
Clarke1880INTFoot6378306.37293.4663
Clarke1880RGS6378249.145293.465
Danish18766377019.27300
Everest1830_1962D6377299.366300.8017
Everest1830_1967D6377276.345300.8017
Everest1830_1973A6377301.243300.8017
Everest1830_1975D6377298.556300.8017
Everest1830_RSO19696377299.151300.8017
Everest1830Definition6377295.664300.8017
Everest1830Modified6377304.063300.8017
GRS19676378160298.2472
GRS1967Modified6378160298.25
GRS19806378137298.2572
GSK20116378136.5298.2564
Helmert19066378200298.3
Hough19606378270297
IAG19756378140298.257
IndonesianNationalSpheroid6378160298.247
International19246378388297
Krassowsky19406378245298.3
NWL9D6378145298.25
Plessis18176376523308.64
PZ906378136298.2578
Struve18606378298.3294.73
WarOffice6378300296
WGS726378135298.26
WGS846378137298.2572

投影方法（gma.crs.ProjMethod）

投影（类）中文名
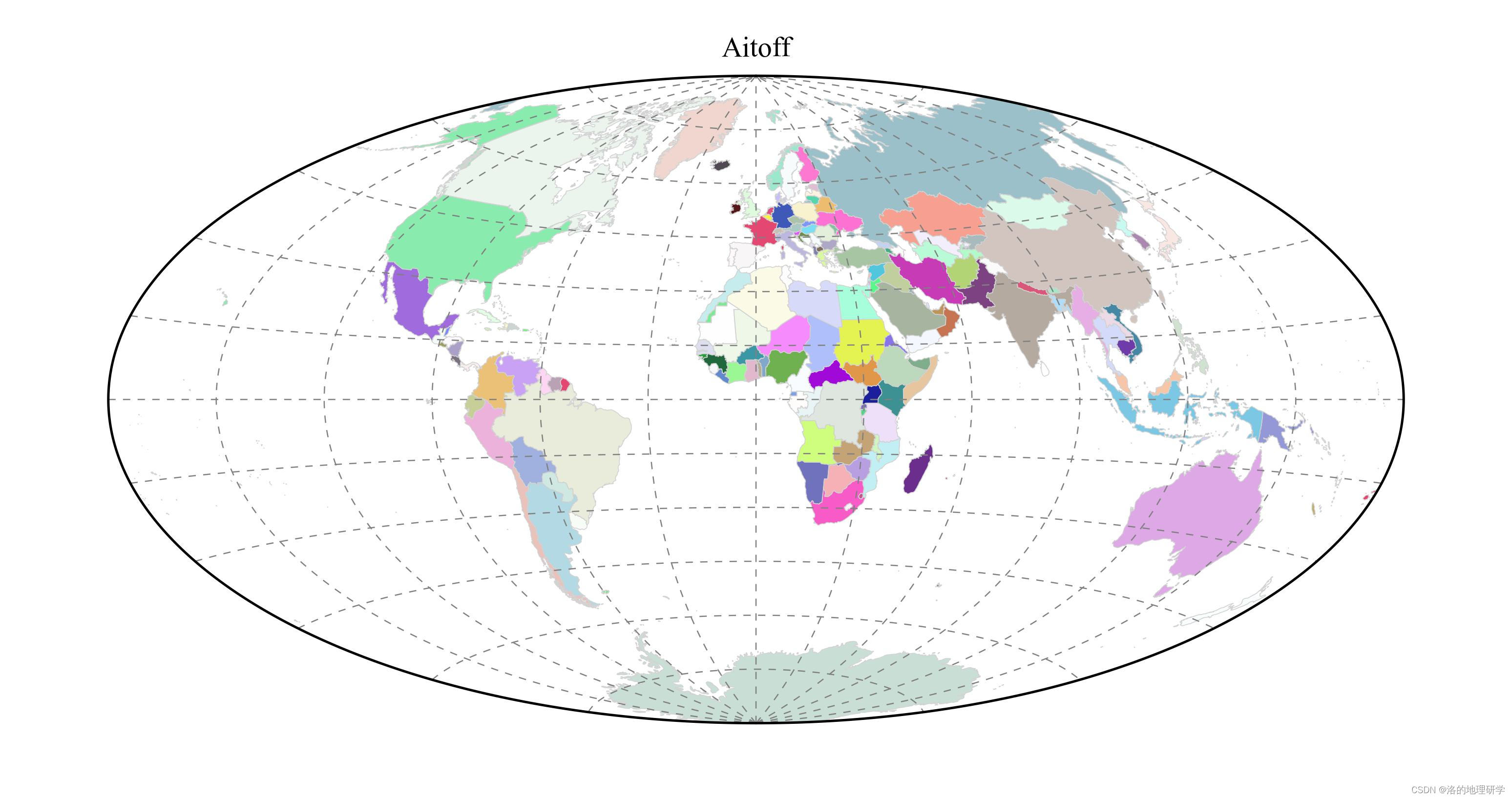
Aitoff埃托夫投影
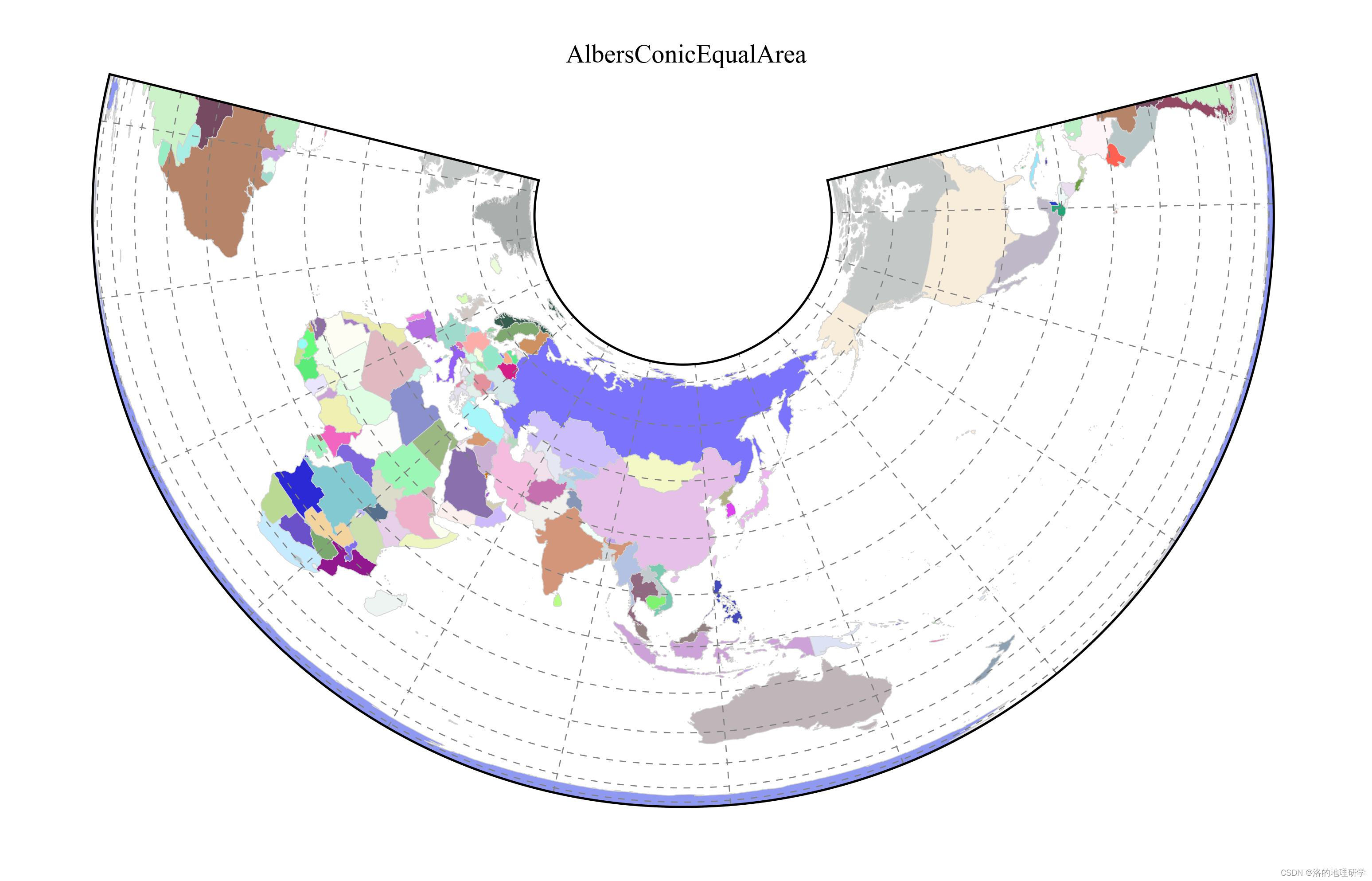
AlbersConicEqualArea阿尔伯斯等积圆锥投影
AzimuthalEquidistant等距方位投影
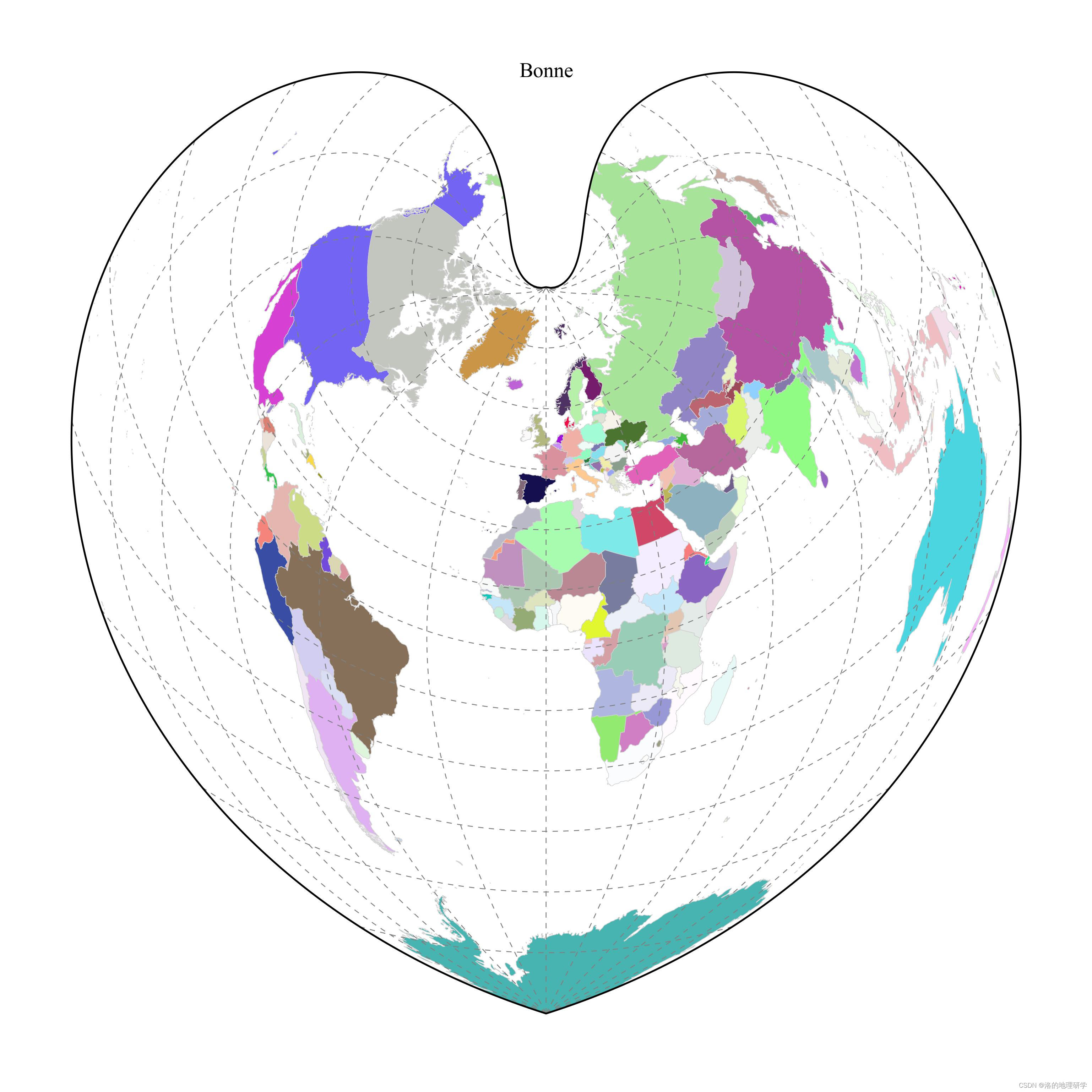
Bonne彭纳
CassiniSoldner卡西尼-斯洛德投影
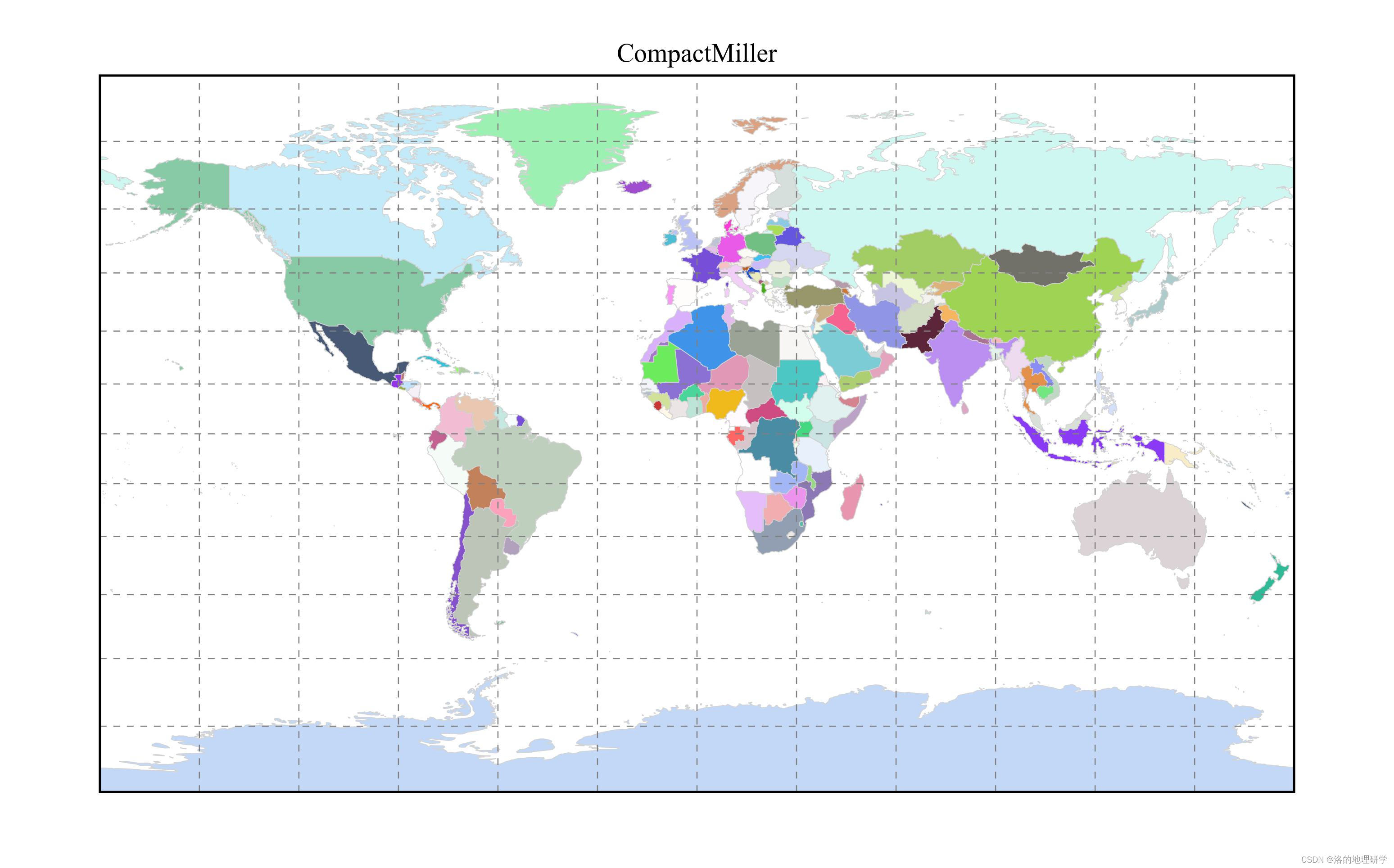
CompactMiller紧凑型米勒投影
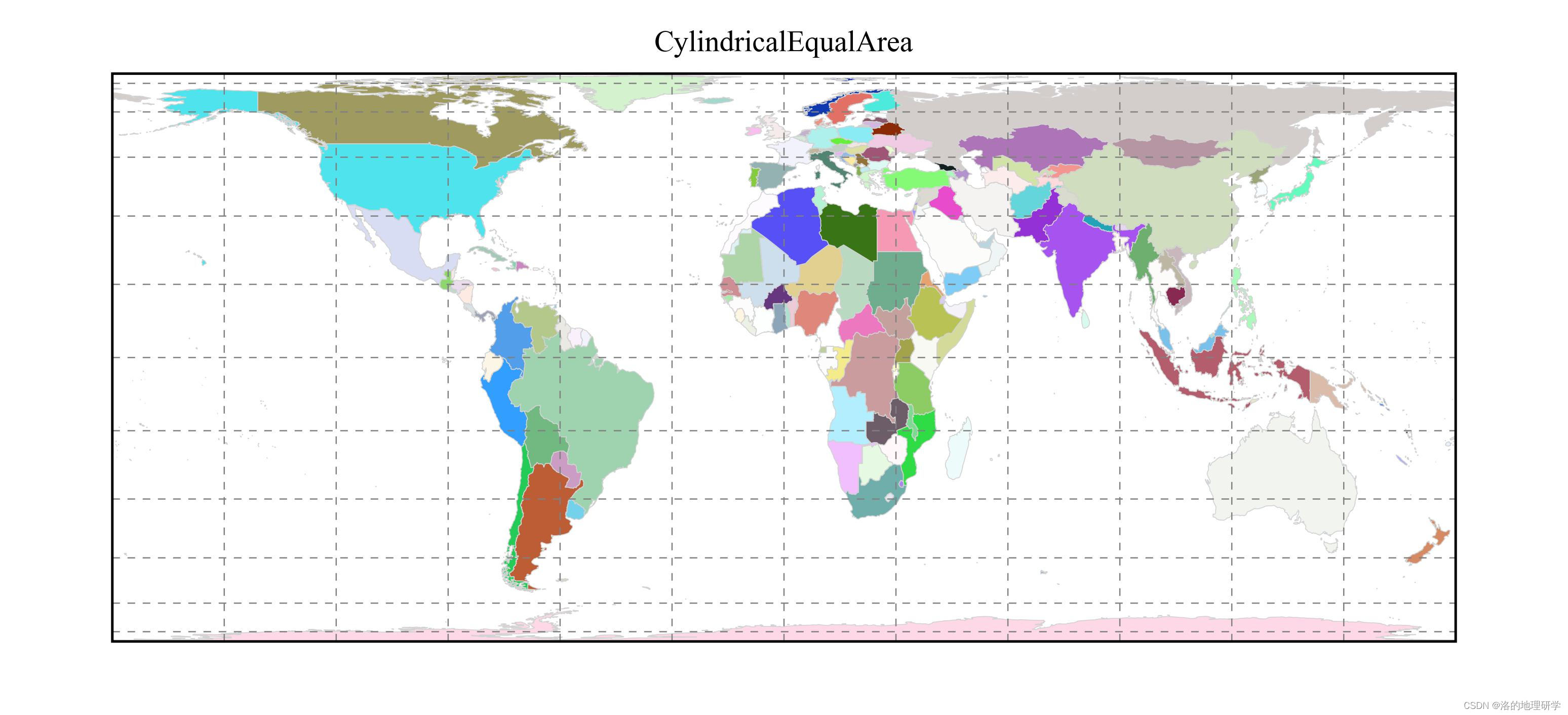
CylindricalEqualArea圆柱等积投影
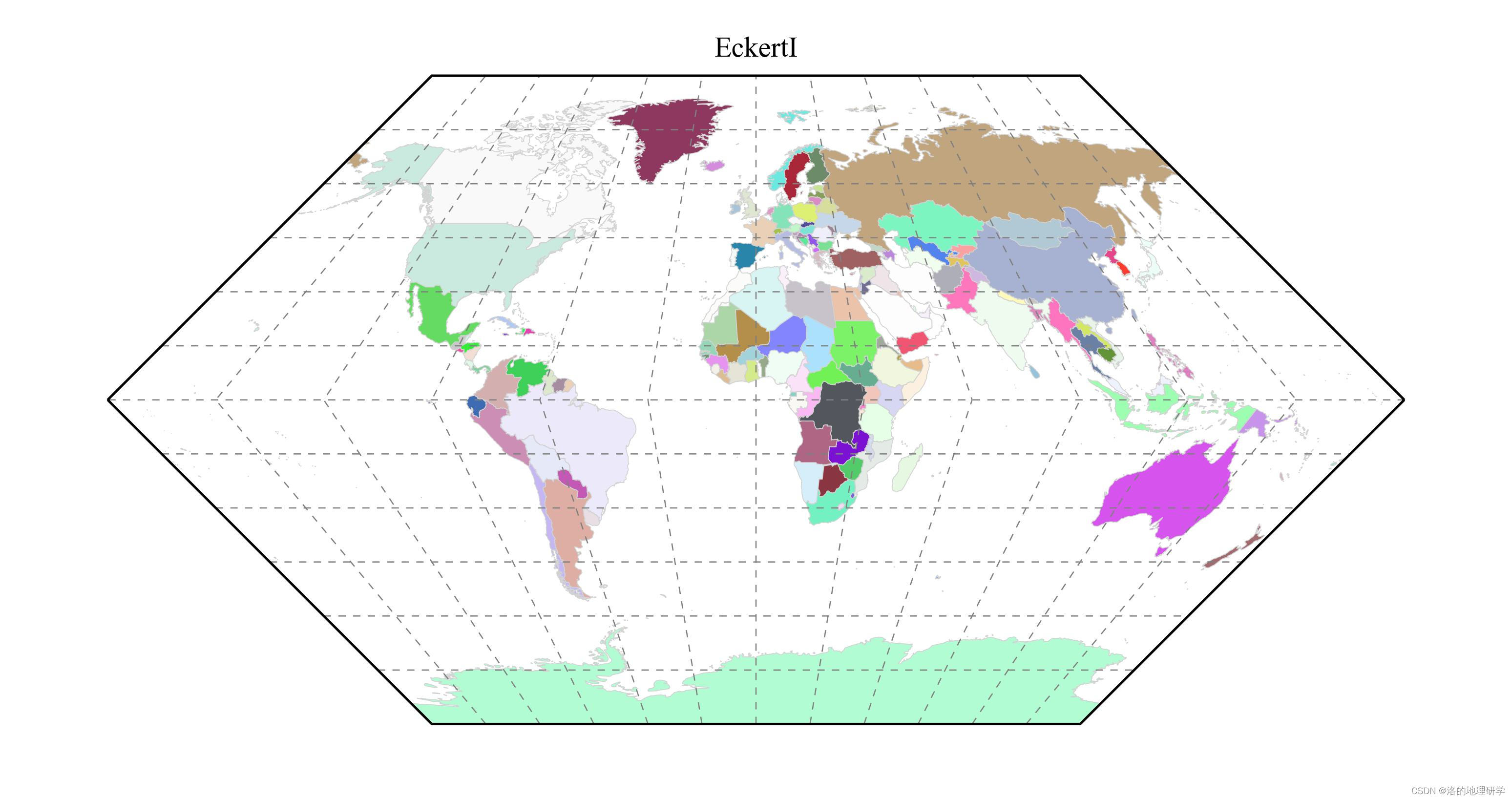
EckertI埃克特 I 投影
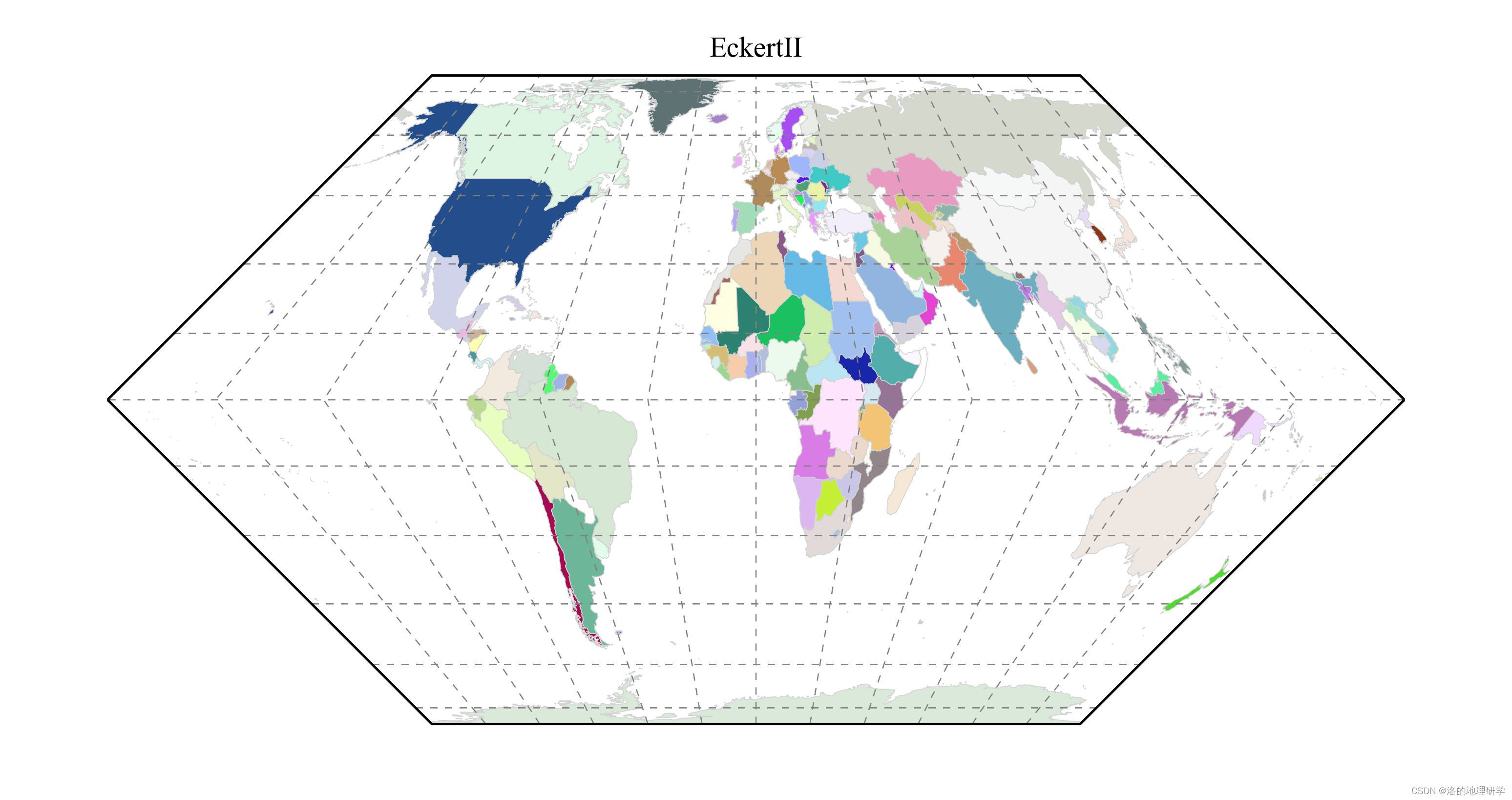
EckertII埃克特 II 投影
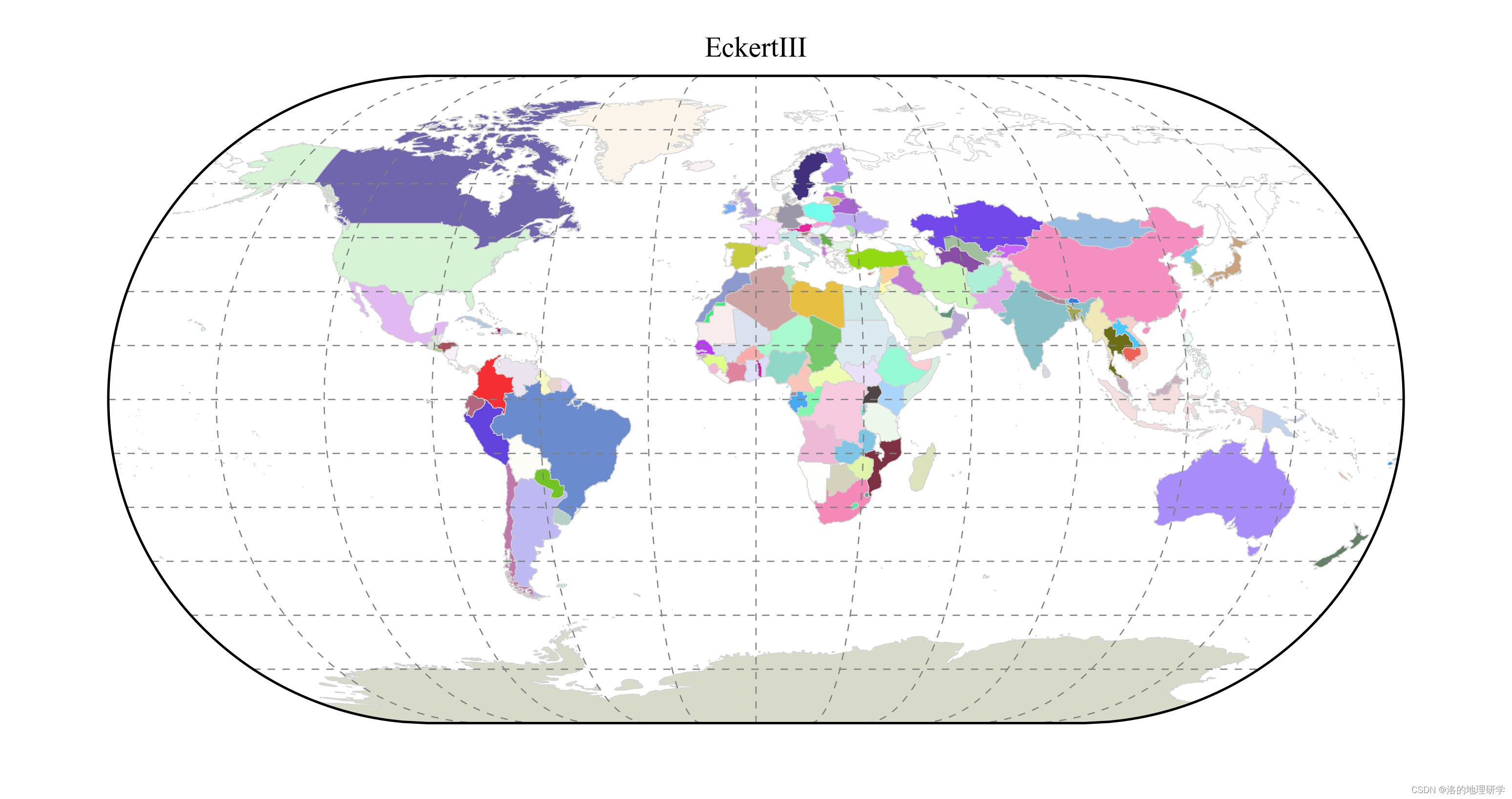
EckertIII埃克特 III 投影
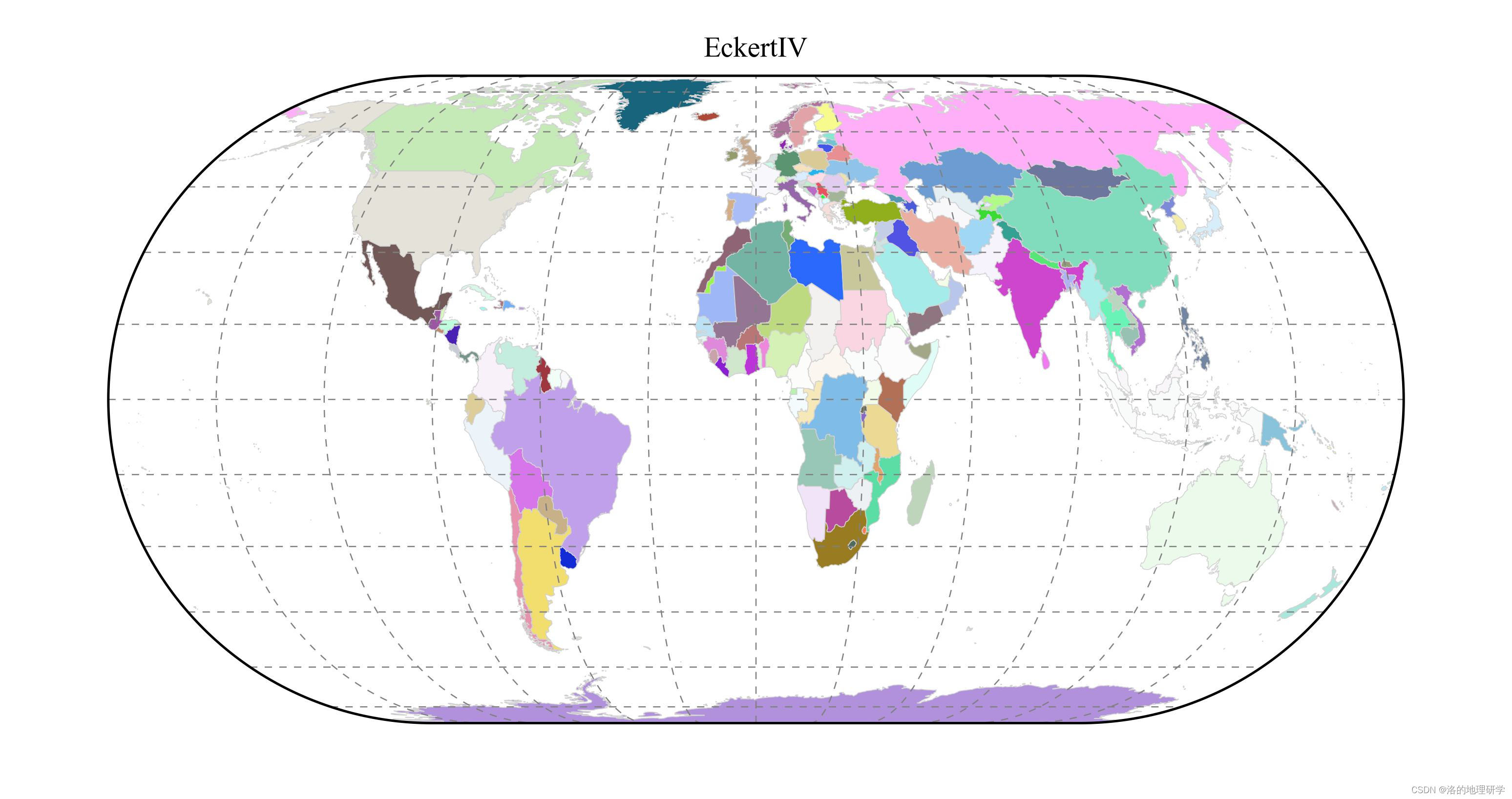
EckertIV埃克特 IV 投影
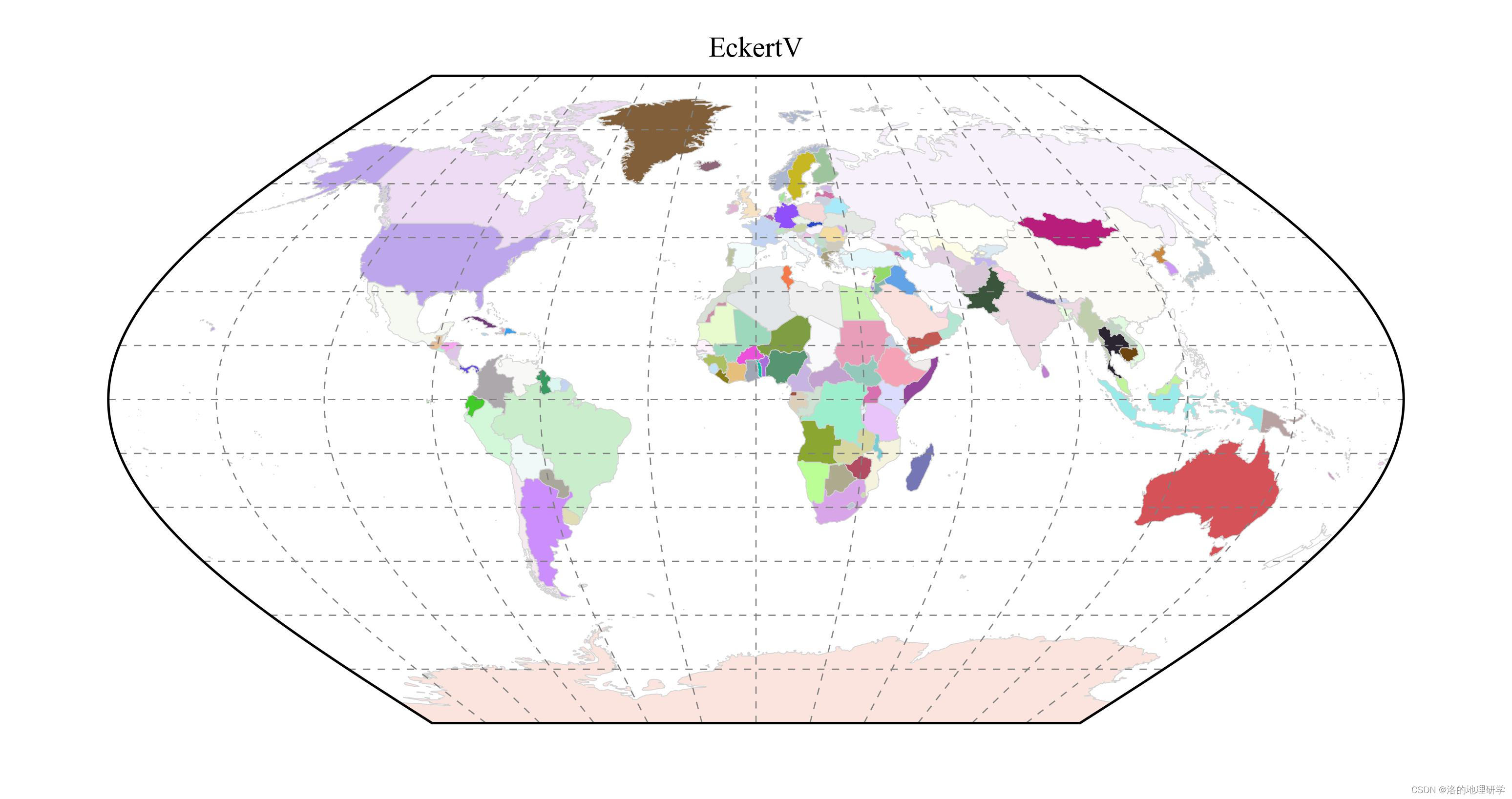
EckertV埃克特 V 投影
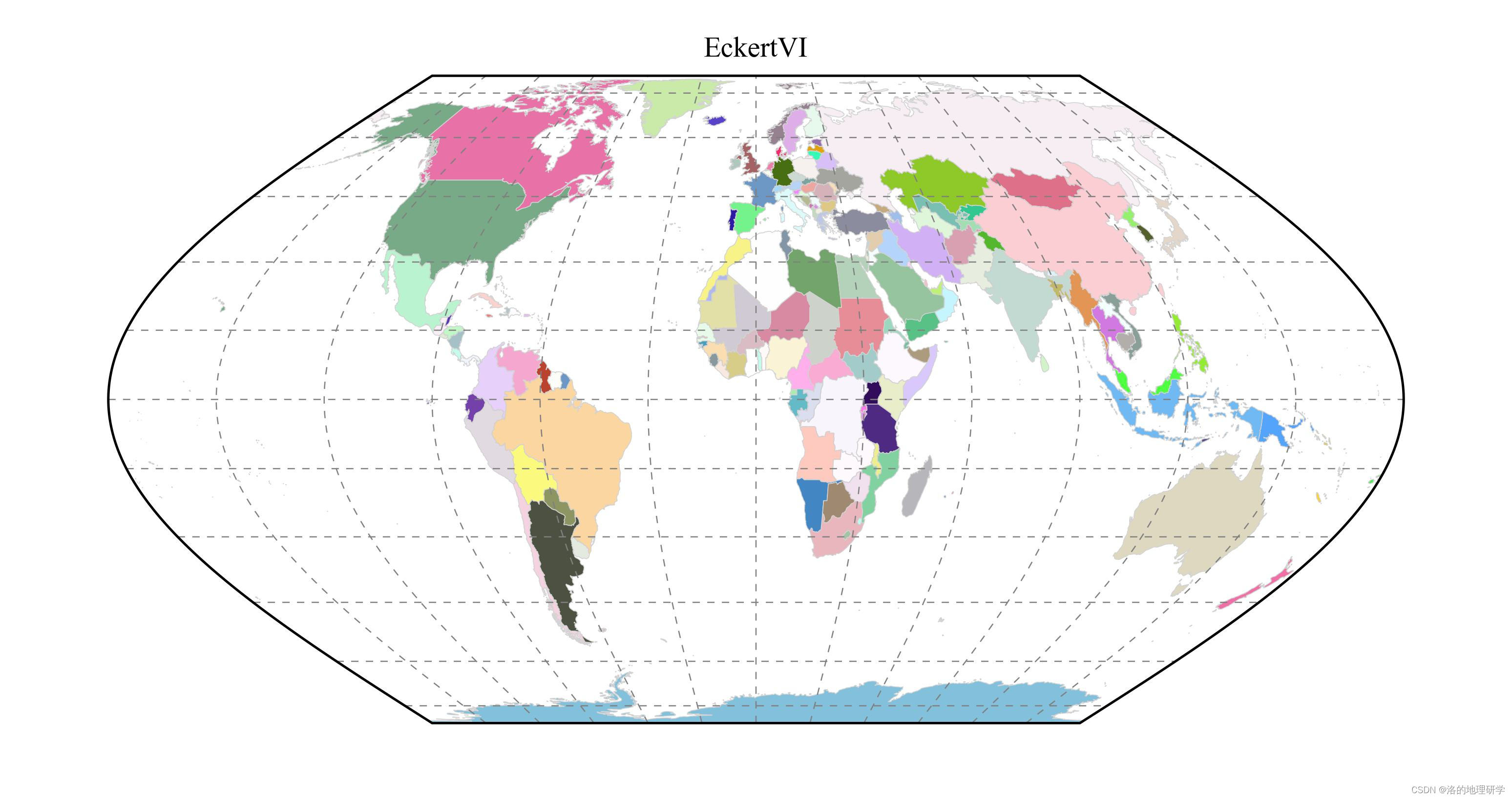
EckertVI埃克特 VI 投影
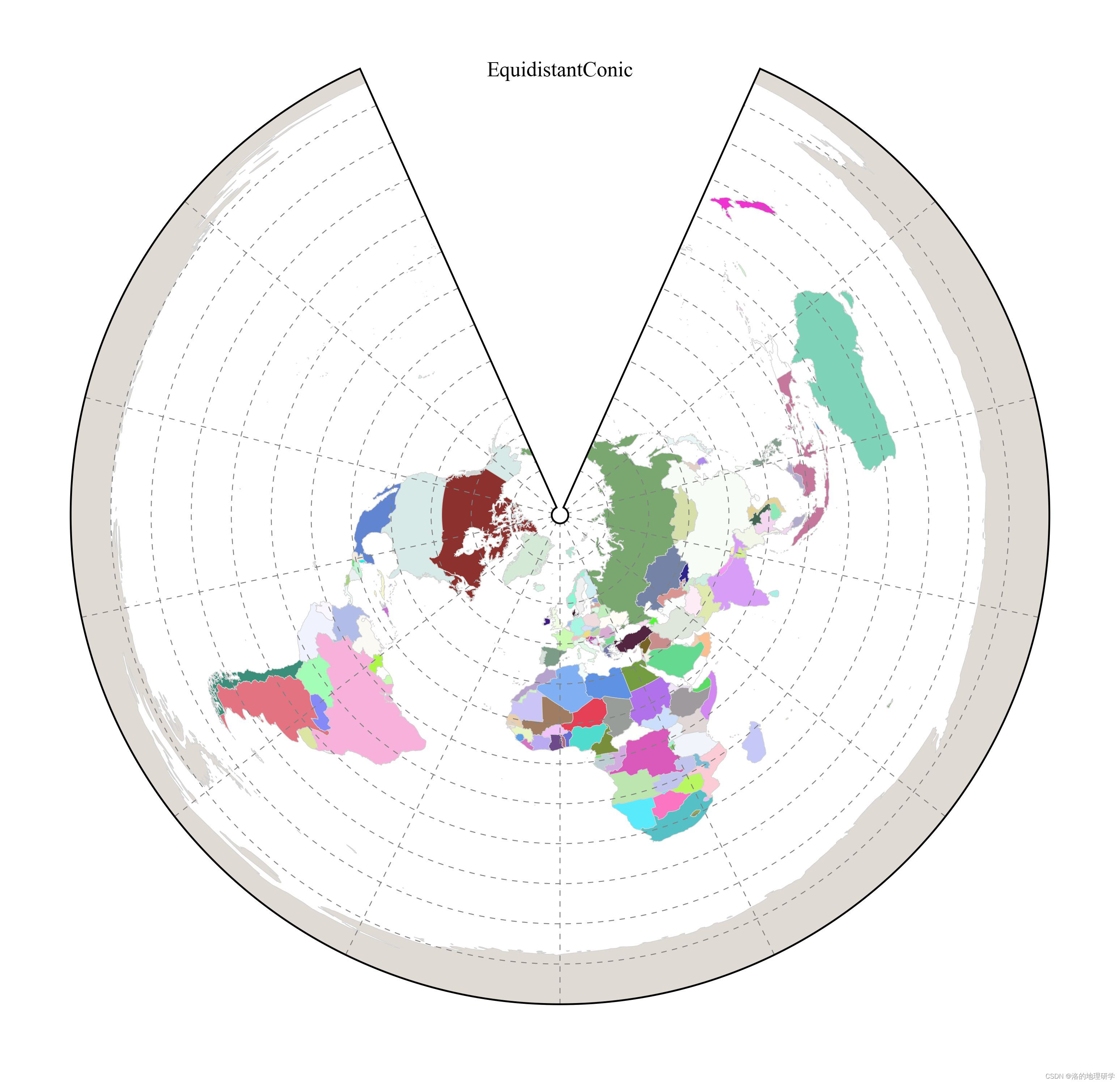
EquidistantConic等距圆锥投影
Equirectangular等距柱状投影
LambertAzimuthalEqualArea兰伯特方位等积投影
Mercator2SP墨卡托投影（2标准纬线）
Mollweide摩尔维特投影
NaturalEarth自然地球投影
Polyconic多圆锥投影
Robinson罗宾森投影
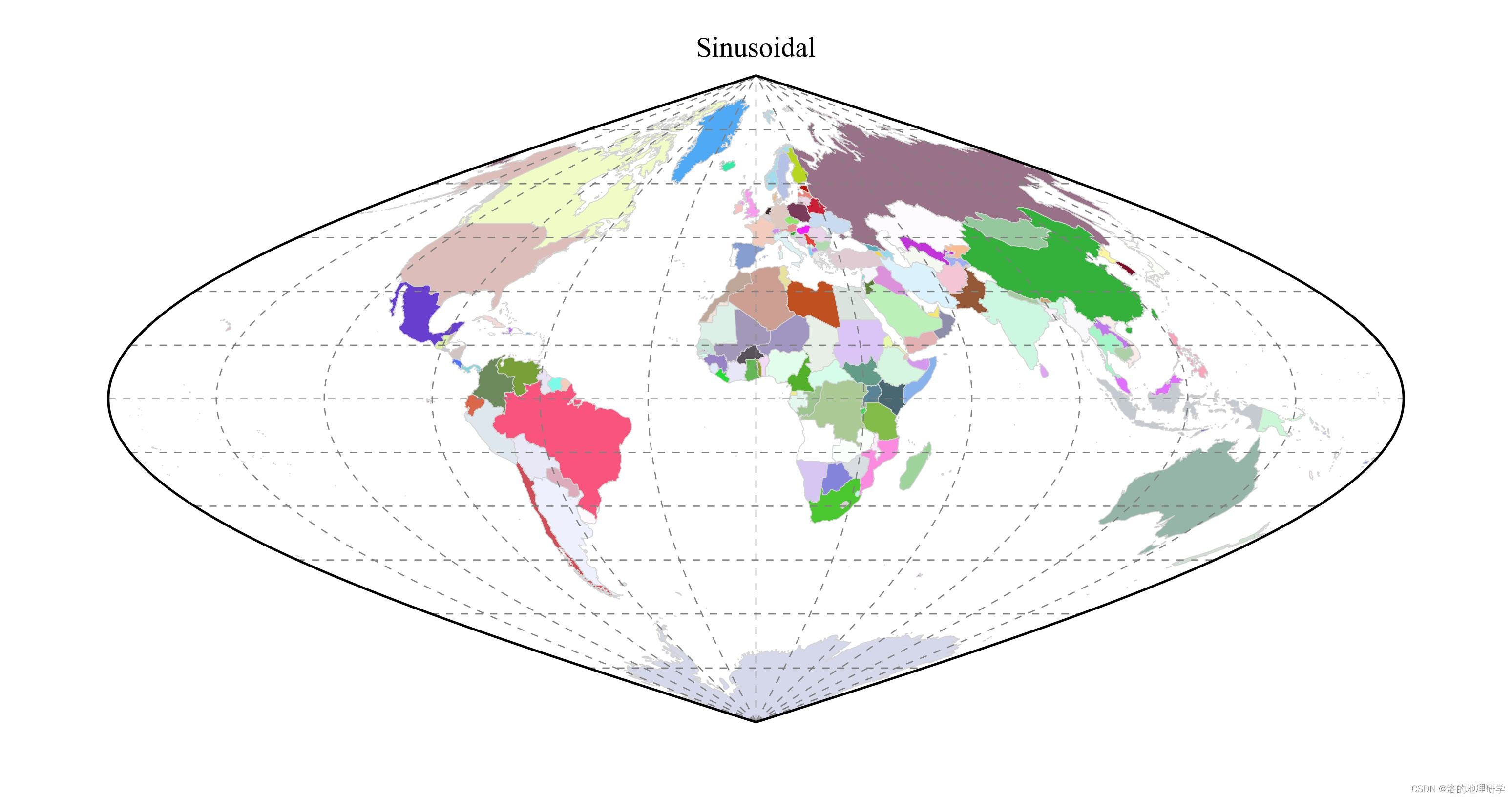
Sinusoidal正弦曲线投影
Stereographic通用极球面投影
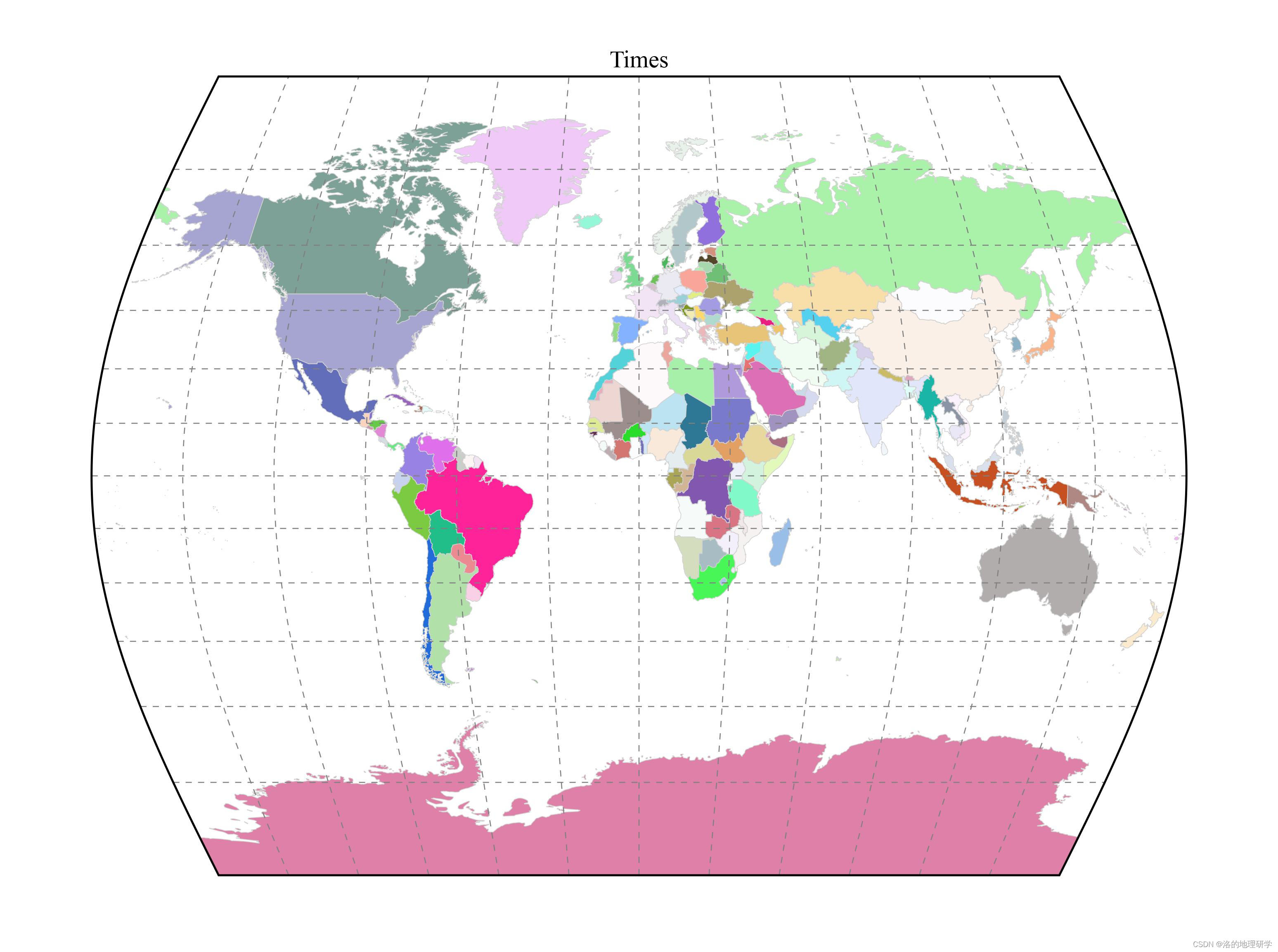
Times泰晤士投影
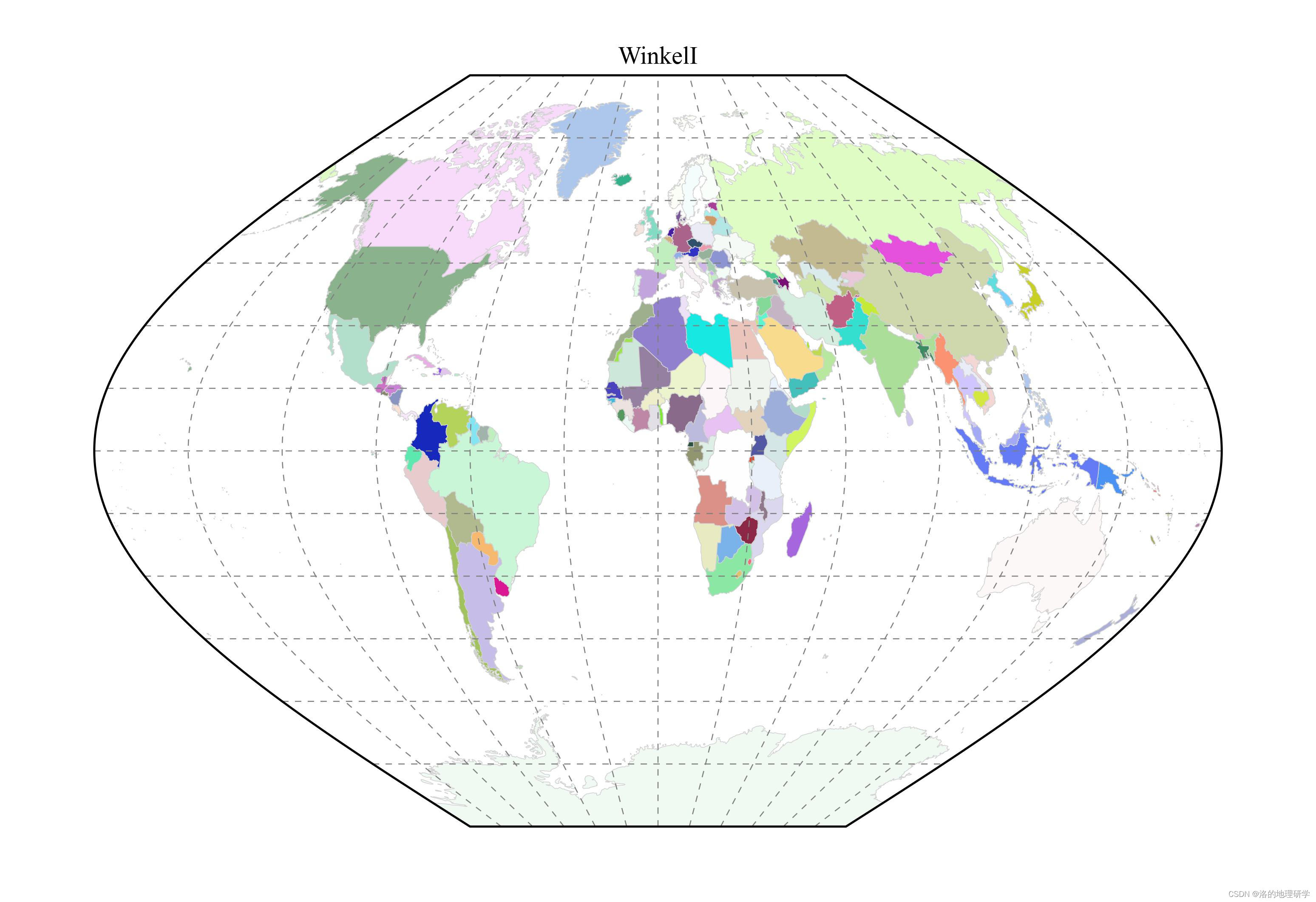
WinkelI温克尔 I 投影
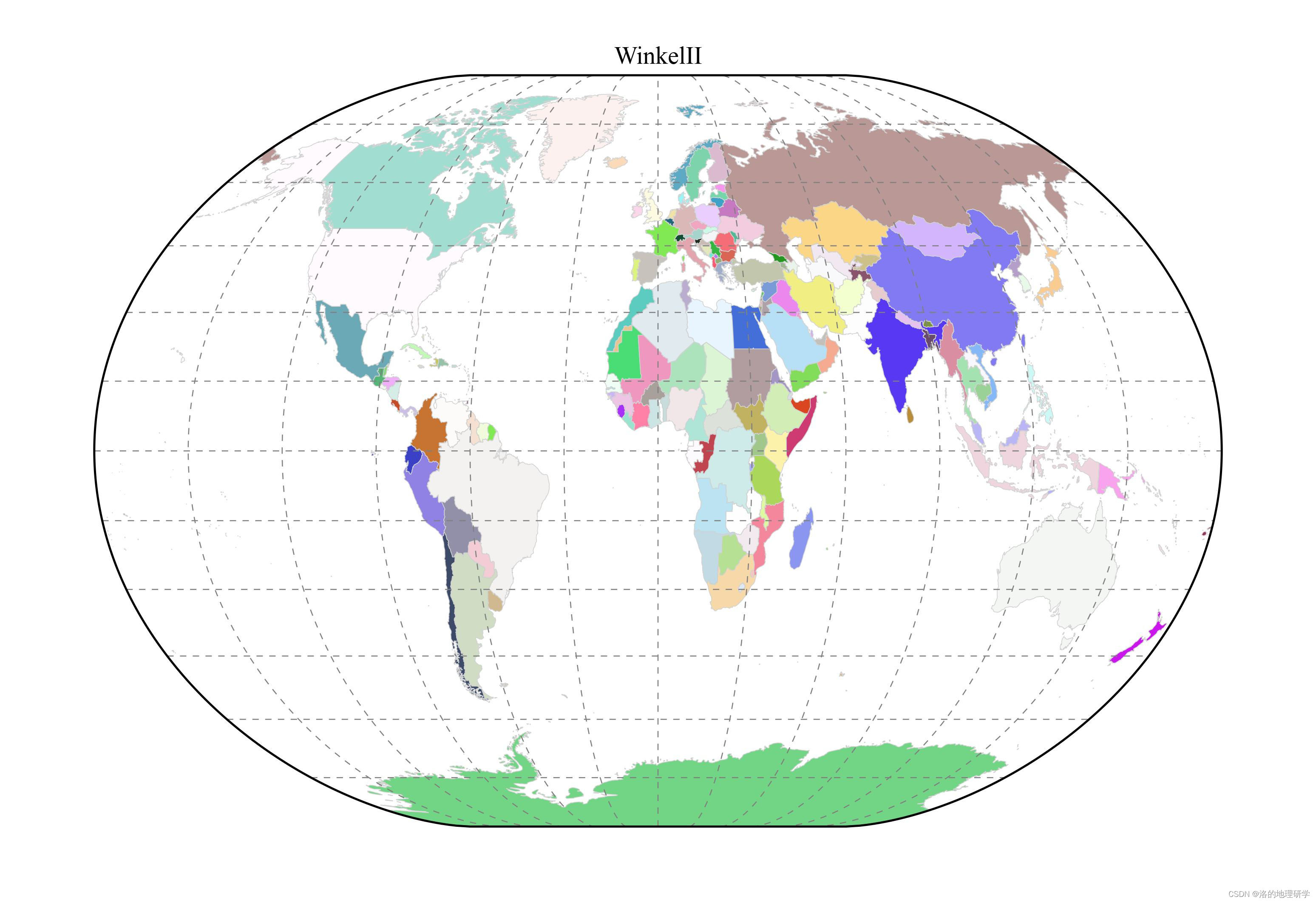
WinkelII温克尔 II 投影

本初子午线（gma.crs.PRIMEMs）

本初子午线名称对应中文名经线（°）
Athens雅典23.7163375
Bern伯尔尼7.439583333
Bogota波哥大-74.08091667
Brussels布鲁塞尔4.367975
Ferro费罗-17.66666667
Greenwich格林尼治0
Jakarta雅加达106.8077194
Lisbon里斯本-9.131906111
Madrid马德里-3.687938889
Oslo奥斯陆10.72291667
Paris巴黎2.337229167
Paris_RGS巴黎2.337208333
ReferenceMeridian参考经线0
Rome罗马12.45233333
Stockholm斯德哥尔摩18.05827778
Luoyang洛阳112.5422641

角度单位（gma.crs.PRIMEMs）

角度单位名称对应中文单位每单位弧度（°）
Arcminute弧分0.000291
Arcsecond弧秒4.85E-06
Degree度0.017453
Grad百分制度0.015708
Gon百分制度0.015708
Microradian微弧度1E-06
Mil6400密尔_64000.000982
Milliarcsecond毫微秒4.85E-09
MinuteCentesimal百分制分0.000157
Radian弧度1
SecondCentesimal百分制秒1.57E-06

线性单位（gma.crs.PRIMEMs）

单位中文对照每单位长度（m）
Meter米1
ClarkesLink克拉克令0.201166
GoldCoastfoot黄金海岸英尺0.3048
USSurveyFoot美国测量英尺0.304801
Foot英尺0.3048
ClarkesFoot克拉克英尺0.304797
link令0.201168
BritishChain英国测链（1922年废弃）20.11676
ClarkesYard克拉克码0.914392
Kilometer千米1000
IndianYard印度码0.914399
BritishChain英国测链（贝诺伊特1895 B）20.11678
BritishYard英国码（希尔斯 1922）0.914398
GermanLegalMeter德国法定米1.000014
BritishChain英国测链（希尔斯 1922）20.11677
BritishFoot英国英尺（希尔斯 1922）0.304799

6. 空间参考（gma.crs.SpatRef）

初始化一个一个空间参考。

7. gma 1.x 遗留函数

AlbersEqualArea
Mollweide
Robinson
CustomGCS

批量绘制世界地图

from gma import crs
from gma.map import plot, inres
import matplotlib.pyplot as plt

# 获取所有支持的投影
ProjMethods = [m for m in dir(crs.ProjMethod) if '__' not in m if 'Utils' not in m]

# 分别绘制 每个投影（默认参数） 下的世界地图
for m in ProjMethods:
    
    # 生成 投影 m 的投影坐标系
    PCS = crs.ProjCS(Name = 'GMA PCS', LinearUnit = 'Meter', ProjMethod = m, GCS = 'WGS84')

    # 1.初始化一个地图框，用于绘图
    MapF = plot.MapFrame(Axes = None, BaseMapProj = PCS, Extent = None)

    # 2.将内置的世界矢量图层添加到地图框
    MapL1 = MapF.AddLayer(inres.WorldLayer.Country, FaceColor = None, LineWidth = 0.2, EdgeColor = 'lightgray', Zorder = 1)
    
    # 3.经纬网
    MapF.AddGridLines(LONRange = (-180, 180, 30))
    
    # 4.地图框
    Frame = MapF.SetFrame(ShowBottom=False,ShowLeft=False,ShowRight=False,ShowTop=False)
    
    MapF.Axes.set_title(m, fontsize = 7, y = 0.93)
    
    # 保存每一张地图
    plt.savefig(f'D:/{m}.jpg' ,bbox_inches='tight', dpi = 600)

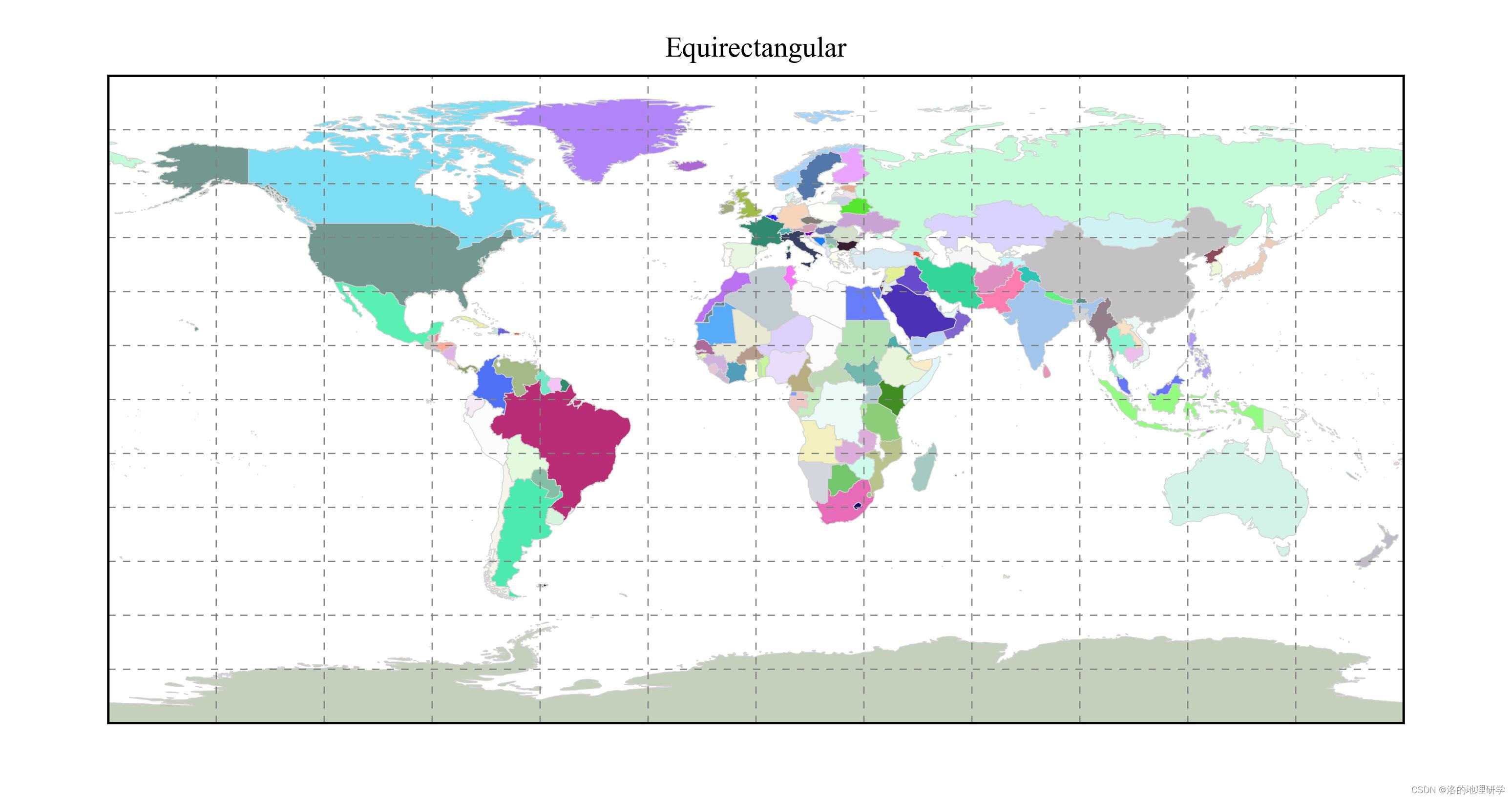
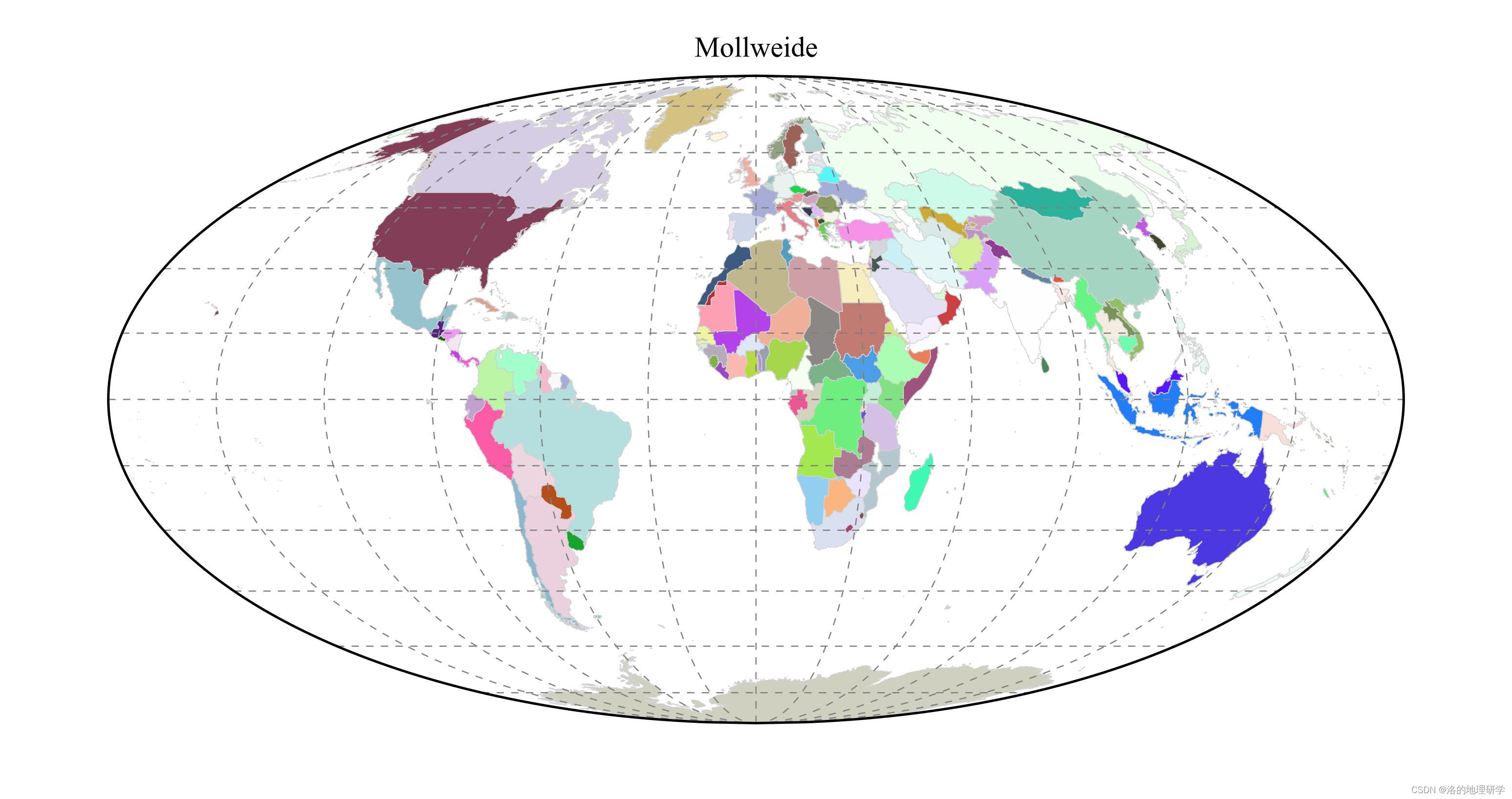
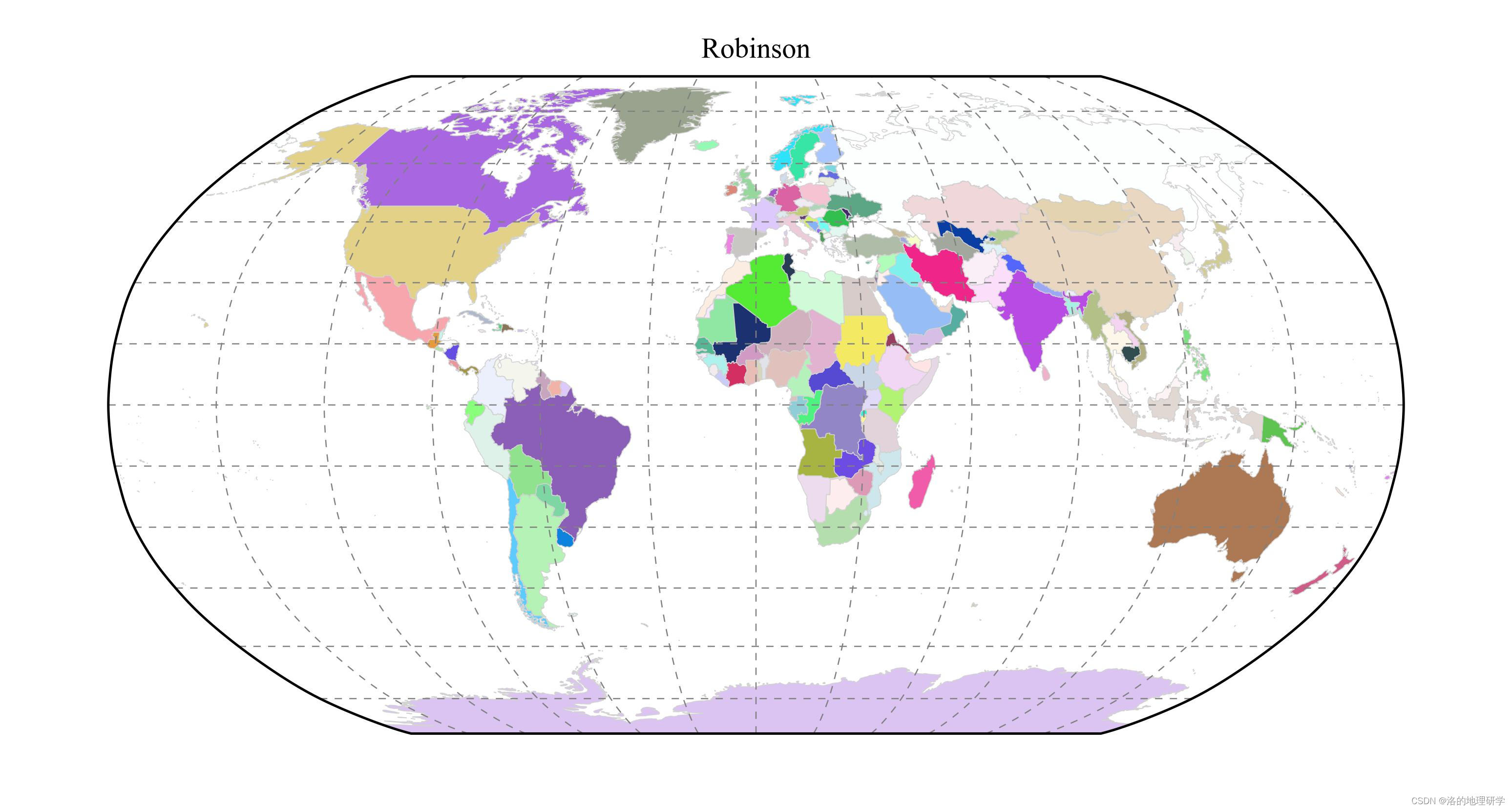
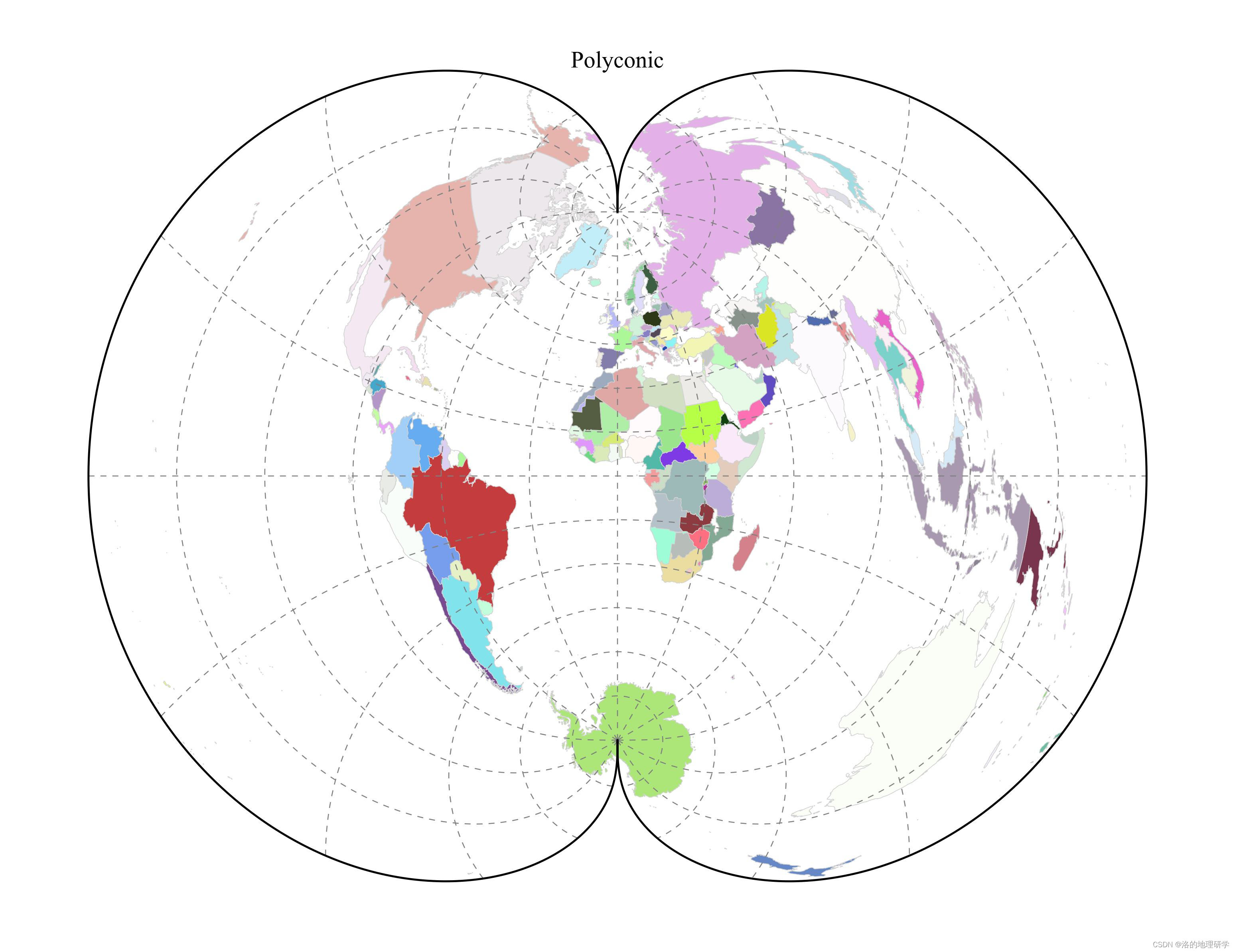
绘图结果展示

部分地图绘制异常，因此不在此处展示


















本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/525531.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

计算机三级网络技术总结(更新中)

计算机三级网络技术总结(更新中)

🍿*★,*:.☆(￣▽￣)/$:*.★* 🍿 🍟欢迎来到前端初见的博文，本文主要讲解我计算机三级网络技术🍟 👨‍🔧 个人主页 : 前端初见 🥞喜欢的朋友可以关注一下&#…
阅读更多...
BEV专栏（二）从BEVFormer看BEV流程（下篇）

BEV专栏（二）从BEVFormer看BEV流程（下篇）

前言 书接上回，在上一篇文章中，我们介绍了BEVFormer这一先进的BEV算法。在本篇文章中，我们将深入探讨BEVFormer的实现细节，旨在帮助读者更深入地理解BEVFormer的工作原理和性能表现。 本教程禁止转载。同时，本教程来自…
阅读更多...
【maven】自定义构建maven的jar包依赖

【maven】自定义构建maven的jar包依赖

前言 自己定义自己的maven的jar包依赖&#xff0c;本地版本。 实现 pom.xml pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSche…
阅读更多...
车载软件架构——闲聊几句AUTOSAR BSW（五）

车载软件架构——闲聊几句AUTOSAR BSW（五）

我是穿拖鞋的汉子，魔都中坚持长期主义的工程师。 老规矩，分享一段喜欢的文字，避免自己成为高知识低文化的工程师： 我们并不必要为了和谐，而时刻保持通情达理；我们需要具备的是，偶尔有肚量欣然承认在某些方面我们可能会有些不可理喻。该有主见的时候能掷地有声地镇得住场…
阅读更多...
车载基础软件——基础软件验证平台（网络管理和诊断）

车载基础软件——基础软件验证平台（网络管理和诊断）

我是穿拖鞋的汉子&#xff0c;魔都中坚持长期主义的工程师。 老规矩&#xff0c;分享一段喜欢的文字&#xff0c;避免自己成为高知识低文化的工程师&#xff1a; 我们并不必要为了和谐&#xff0c;而时刻保持通情达理&#xff1b;我们需要具备的是&#xff0c;偶尔有肚量欣然承…
阅读更多...
部署packstack及问题总结

部署packstack及问题总结

目录 一、部署packstack 1.1 简介 1.2 性能搭配 1.3 准备工作 1.4 安装 二、出现的问题 2.1 安装中断临时文件 2.2 提示某个安装包出错 2.3 leatherman版本太高 三、安装成功 一、部署packstack 1.1 简介 对于openstack初学者而言&#xff0c;传统部署openstack流程…
阅读更多...
MQ-rabbitMQ_基础篇

MQ-rabbitMQ_基础篇

MQ-rabbitMQ_基础篇 1.MQ1.1什么是MQ1,2应用 2.常见消息中间件协议&#xff08;模型&#xff09;2.1JMS模型&#xff08;协议&#xff09;2.2AMQP协议 3.RabbitMQ3.1六种工作模式3.1.1Hello Word简单模式3.1.2word queues 工作队列能者多劳 3.1.3Publish/Subscribe 发布与订阅模…
阅读更多...
在SwissTargetsPrediction数据库中预测成分靶点

在SwissTargetsPrediction数据库中预测成分靶点

1.对筛选的多肽成分进行靶点预测&#xff1a; ①用Uniport中的蛋白进行一系列操作&#xff08;水解&#xff0c;挑选2~8短肽&#xff0c;活性预测&#xff0c;毒性&#xff0c;过敏性预测&#xff0c;胃肠吸收度&#xff0c;半衰期和苦味的预测、生物活性功能预测&#xff09;…
阅读更多...
mybatis连接池源码分析

mybatis连接池源码分析

文章目录 前言一、PooledDataSourceFactory二、获取连接三、归还连接 前言 其实大部分连接池的代码都大同小异&#xff0c;总体获取连接&#xff0c;归还连接逻辑大都相同。希望通过阅读本文章&#xff0c;能给你带来帮助。 测试用例 public void testMybatis()throws Excepti…
阅读更多...
深入篇【C++】类与对象：运算符重载详解

深入篇【C++】类与对象：运算符重载详解

深入篇【C】类与对象&#xff1a;运算符重载详解 ⏰一.运算符重载&#x1f553;1.<运算符重载&#x1f550;2.>运算符重载&#x1f552;3.运算符重载&#x1f551;4.运算符重载①.格式1.改进12.改进2 ②.默认成员函数1.功能2.不足 &#x1f553;5.<运算符重载&#x1…
阅读更多...
学内核之十九：Linux文件系统结构大蓝图

学内核之十九：Linux文件系统结构大蓝图

目录 一&#xff1a;参考资料 二&#xff1a;整理的原因及基本原则 三&#xff1a;Linux文件系统大蓝图 四&#xff1a;补充说明 一&#xff1a;参考资料 博主梳理的关于文件系统的基础知识&#xff1a; 7.5 文件系统_定义_龙赤子的博客-CSDN博客 博主转载的关于page cac…
阅读更多...
深入理解深度学习——正则化（Regularization）：参数范数惩罚

深入理解深度学习——正则化（Regularization）：参数范数惩罚

分类目录&#xff1a;《深入理解深度学习》总目录 正则化在深度学习的出现前就已经被使用了数十年。线性模型&#xff0c;如线性回归和逻辑回归可以使用简单、直接、有效的正则化策略。许多正则化方法通过对目标函数 J J J添加一个参数范数惩罚 Ω ( θ ) \Omega(\theta) Ω(θ…
阅读更多...
三、Neo4j 源码研究系列 - 持久化

三、Neo4j 源码研究系列 - 持久化

version: v-2023051401 author: 路__ 说到数据库&#xff0c;那么离不开的模块就是持久化&#xff08;Persistence&#xff09;&#xff0c;数据持久化是数据库不可缺少的重要组成模块之一。可以说一个数据库少了持久化功能&#xff0c;可以说这个数据库就不足以称为数据库。…
阅读更多...
并查集：解密算法面试中的常客

并查集：解密算法面试中的常客

文章目录 1. 并查集原理&#x1f351; 举例说明&#x1f351; 并查集的应用 2. 并查集实现&#x1f351; 接口总览&#x1f351; 构造函数&#x1f351; 查询操作&#x1f345; 代码实现 &#x1f351; 合并操作&#x1f345; 动图演示&#x1f345; 代码实现 &#x1f351; 判…
阅读更多...
Linux文件打开函数open()

Linux文件打开函数open()

#include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #include <stdio.h> int main(void) {int fd -1; /*这个整数用来存放文件描述符*/char filename[] "good.txt"; /*打开的文件名&#xff0c;是一个字符数组…
阅读更多...
String类 [下]

String类 [下]

目录 一、拷贝构造和赋值重载的传统写法和现代写法 0x01 拷贝构造的传统写法 0x02 拷贝构造的现代写法 0x03 赋值重载的传统写法 0x04 赋值重载的现代写法 0x05 总结 二、 增删改查之后的string 0x01 成员函数swap: 0x02 reserve&#xff1a;改变容量 0x03 push_back: 尾…
阅读更多...
带你深入理解Java异常

带你深入理解Java异常

&#x1f495;“人生就像一盘棋&#xff0c;有时候你慢一步&#xff0c;就输掉了一局。但只要你不停止思考和行动&#xff0c;就永远有机会翻盘。”&#x1f495; &#x1f43c;作者&#xff1a;不能再留遗憾了&#x1f43c; &#x1f386;专栏&#xff1a;Java学习&#x1f38…
阅读更多...
《计算机网络——自顶向下方法》精炼——3.4.1-3.4.3

《计算机网络——自顶向下方法》精炼——3.4.1-3.4.3

聪明出于勤奋,天才在于积累。——华罗庚 文章目录 对协议的进一步改进rdt2.1rdt2.2rdt3.0&#xff1a;含有比特差错和丢包的可靠数据传输协议 流水线协议回退n步&#xff08;GBN&#xff09; 对协议的进一步改进 rdt2.1 在上一篇文章中&#xff0c;我们讲到对于产生比特差错的…
阅读更多...
A2-RIDE Long-tailed recognition by routing diverse distribution-aware experts

A2-RIDE Long-tailed recognition by routing diverse distribution-aware experts

文章目录 0. Abstract1. Introduction2. Related Works3. RIDE&#xff1a;ROUTING DIVERSE DISTRIBUTION-AWARE EXPERTS4. Experiments5. Summary论文总结长尾数据分布 (Long-tailed Data Distribution)RIDE方法及模型1. **Multi-expert framework**2. **Routing diversified …
阅读更多...
RabbitMQ如何保证顺序消费

RabbitMQ如何保证顺序消费

目录标题 生产者有序的情况下如何保证顺序生产单个消费者多个消费者 生产者无序的情况下消息返回队列消息不返回队列 生产者有序的情况下 如何保证顺序生产 单一生产者&#xff1a;消息生产的顺序性仅支持单一生产者。 串行发送&#xff1a;如果生产者采用多线程并行发送&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023