文章目录
- 1. 并查集原理
- 🍑 举例说明
- 🍑 并查集的应用
- 2. 并查集实现
- 🍑 接口总览
- 🍑 构造函数
- 🍑 查询操作
- 🍅 代码实现
- 🍑 合并操作
- 🍅 动图演示
- 🍅 代码实现
- 🍑 判断操作
- 🍅 动图演示
- 🍅 代码实现
- 🍑 集合个数
- 🍅 代码实现
- 3. 并查集路径压缩
- 🍑 举例说明
- 🍅 动图演示
- 🍅 代码实现
- 4. 并查集应用
- 🍅 省份数量
1. 并查集原理
在一些应用问题中,需要将 n 个不同的元素划分成一些不相交的集合。开始时,每个元素自成一个单元素集合,然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。
适合于描述这类问题的抽象数据类型称为 并查集(union-find set)
🍑 举例说明
某 BAT 公司今年校招预计在全国总共招生 10 人,北京招 4 人,成都招 3 人,武汉招 3 人,这 10 个人来自不同的学校,起先互不相识,每个学生都是一个独立的小团体,现在给这些学生进行编号 {0, 1, 2, 3, 4, 5, 6, 7, 8, 9},并给以下数组用来存储该小集体,数组中的数字代表该小集体中具有成员的个数(-1 就表示没有)。
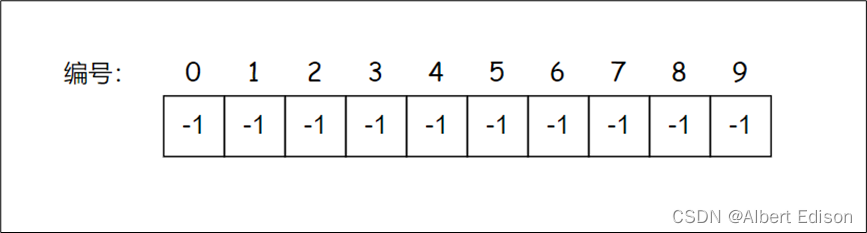
毕业后,学生们各自要去公司上班,每个地方的学生自发组织成小分队一起上路,于是:北京学生小分队 s1 = {0, 6, 7, 8},成都学生小分队 s2 = {1, 4, 9},武汉学生小分队 s3 = {2, 3, 5},分队里的成员就相互认识了,10 个人形成了三个小团体。
组好队以后,它们又各自选出了队长,假设 0,1,2 分布担任自己队的队长,负责大家的出行。
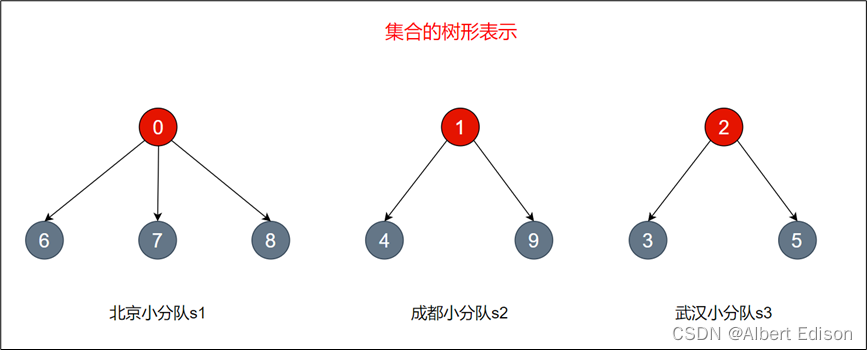
一趟火车之旅后,每个小分队成员就互相熟悉,称为了一个朋友圈。
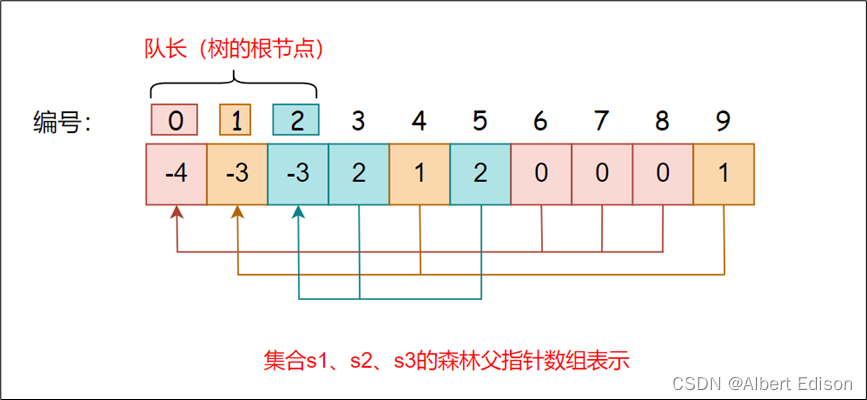
建立集合的规则:{0, 6, 7, 8} 是一个集合,那么可以 选取最小的值 0 作为树的根(也可以选取最大的),然后 0 就和 6、7、8 建立父子关系,此时 6、7、8 的状态由 -1 变成了 0,因为 0 是它们的根节点,那么 0 的状态由 -1 变成了 -4,因为它有三个孩子,并且这个三个孩子的初始状态是 -1,所以 -1 + -1 + -1 + -1 = -4
从上图可以看出:
- 编号为
6, 7, 8的同学属于 0 号小分队,该小分队中有 4 人(包含队长 0) - 编号为
4, 9的同学属于 1 号小分队,该小分队有 3 人(包含队长 1) - 编号为
3, 5的同学属于 2 号小分队,该小分队有 3 个人(包含队长 2)
仔细观察数组中的元素,可以得出以下结论:
- 数组的下标对应集合中元素的编号
- 数组中,一个位置的值如果是负数,那么这个值就是树的根,这个负数的绝对值就是这颗树的集合个数。
- 数组中,一个位置的值如果是非负数,那么这个值表示,该元素的父亲在数组中的下标(比如 6 的元素为 0,说明 0 下标是 6 的父亲)
那么在公司工作一段时间后,北京小分队中的 8 号同学与成都小分队的 1 号同学就成为了好朋友,那么各自两个小圈子的学生相互介绍,最后成为了一个小圈子:
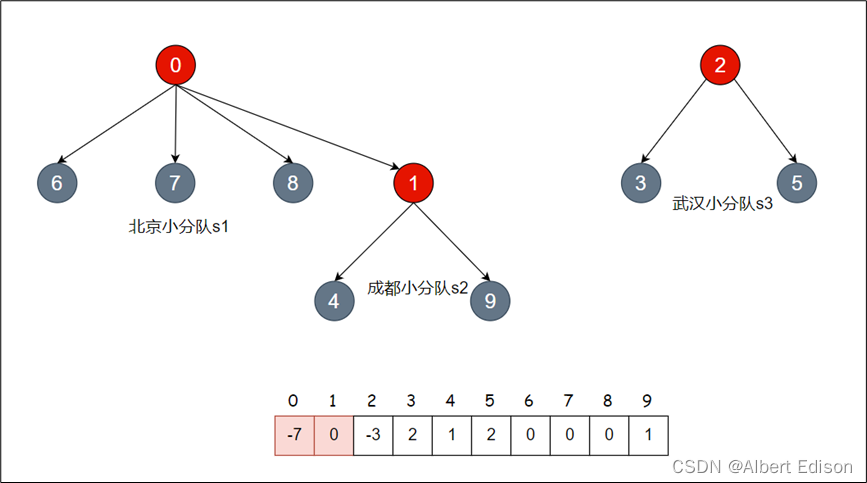
现在 0 集合有 7 个人,2 集合有 3 个人,所以总共有两个朋友圈。
那么 s1 和 s2 是如何合并呢???我们现在要合并 1 号同学和 8 号同学:
- 先找到 1 号同学所在的树的根
- 然后找到 8 号同学所在的树的根
- 接着两颗树的根节点进行比较,小的那棵树就合并到大的树下去(也可以大的合并到小的下面去),1 号同学的根节点就是它自己,8 号同学的根节点为 0,那么就把根节点为0的树链接到根节点1的下面
- 最后更新根节点 0 的元素个数,因为根节点为 0 的树最开始就有 3 个节点,再加上 s2 集合的个数,所以由
-4变成了-7,那么此时 1 的根节点已经变成 0 了,所以要存在 0。
🍑 并查集的应用
通过以上例子可知,并查集一般可以解决一下问题:
(1)查找元素属于哪个集合
- 沿着数组表示树形关系以上一直找到根(即:树中中元素为负数的位置)
(2)查看两个元素是否属于同一个集合
- 沿着数组表示的树形关系往上一直找到树的根,如果根相同表明在同一个集合,否则不在
(3)将两个集合归并成一个集合
- 将两个集合中的元素合并
- 将一个集合名称改成另一个集合的名称
(4)集合的个数
- 遍历数组,数组中元素为负数的个数即为集合的个数。
2. 并查集实现
🍑 接口总览
对于并查集的实现,我们可以不用映射关系这么复杂的结构,假设现在只有下标,那么可以选择用 vector 来存储。
代码示例
class UnionFindSet
{
public:
// 构造函数
UnionFindSet(size_t n);
// 查询操作(找到x所在树的根节点)
int FindRoot(int x);
// 合并操作(合并x1和x2)
void Union(int x1, int x2);
// 判断操作(判断x1和x2是否在同一个集合内)
bool InSet(int x1, int x2);
// 集合个数(找到这个数组有多少个集合)
size_t SetSize();
private:
vector<int> _ufs; // 数组
};
🍑 构造函数
因为是用 vector 来存储的,所以在初始化列表的时候,直接开辟长度为 n 的数组,并初始化为 -1。
代码示例
// 构造函数
UnionFindSet(size_t n)
:_ufs(n, -1)
{}
🍑 查询操作
如何找到 x 的根节点呢?很简单:
- 如果 x 位置是一个负数,那么说明 x 就是根节点
- 如果 x 位置不是一个负数,那么说明就要去找根节点
- 先把 x 的值赋给 parent,然后用 parent 作下标去访问该位置的值
- 如果
_ufs[parent] >= 0,说明就要跳到_ufs[parent]的位置再去查找,也就是parent = _ufs[parent]
假设我们要找 9 的根节点:
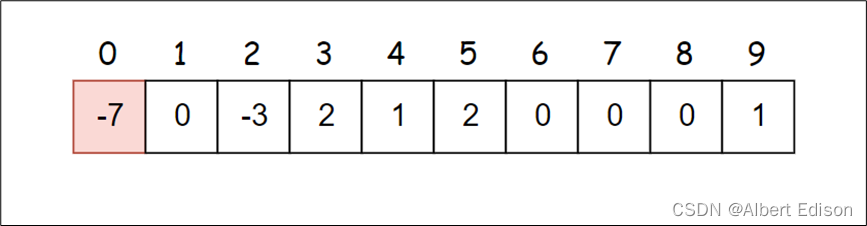
9 位置里面存储的值为 1,说明 1 就是 9 的父亲的下标,那么就去看下标 1 位置里面存储的值,判断是否为一个负数。
1 位置里面存储的值为 0,说明 0 不是 9 的根节点,但是 0 是 1 的父亲的下标,那么就去看下标 0 位置里面存储的值,判断是否为一个负数。
0 位置里面存储的值为 -7,而 -7 小于 0,说明 0 就是 9 的根节点,直接返回即可。
🍅 代码实现
代码示例
// 查询操作(找到x所在树的根节点)
int FindRoot(int x)
{
int parent = x; // x下标存储的值是它父亲的下标
while (_ufs[parent] >= 0) // 当父亲位置的值大于等于0,进入循环
{
parent = _ufs[parent];
}
// 程序走到这里,说明父亲位置里面存的是一个负数,即x的根节点
return parent;
}
🍑 合并操作
如何合并 x1 和 x2 呢?
- 先找到 x1 的根节点 root1,再找到 x2 的根节点 root2,然后判断是否在同一个集合
- 如果 root1 等于 root2,说明 x1 和 x2 在同一个集合,那么就不需要合并
- 如果 root1 不等于 root2,说明需要合并
- 这里统一成把大的根节点所在的树合并到小的里面去,假设 root2 大,root1 小
- 首先要把 root2 里面的节点个数加到 root1 里面去:
_ufs[root1] += _ufs[root2] - 然后修改 root2 的根节点,此时 root2 位置里面存储的就是它的父亲,也就是 root1,即
_ufs[root2] = root1
- 首先要把 root2 里面的节点个数加到 root1 里面去:
🍅 动图演示
如下图所示:合并 3 和 8 两颗子树

🍅 代码实现
代码示例
// 合并操作(合并x1和x2)
void Union(int x1, int x2)
{
int root1 = FindRoot(x1); // 找到x1的根节点
int root2 = FindRoot(x2); // 找到x2的根节点
// 如果root1和root2相等,说明它俩本身就是在一个集合,那么就没必要合并了
if (root1 == root2)
return;
// 把小的根节点合并到大的根节点里面去
// 默认root2大,root1小
if (root1 > root2) // 如果root1大,root2小
swap(root1, root2); // 那么就交换
_ufs[root1] += _ufs[root2]; // 把root2所在树的节点个数添加到root1里面去
_ufs[root2] = root1; // root2位置存在的根节点为root1
}
🍑 判断操作
如何判断 x1 和 x2 是否在同一个集合内呢?
很简单:
- 先分别找到 x1 和 x2 的根节点
- 如果根节点相等,说明在一个集合;反之,不在一个集合。
🍅 动图演示
现在我们要判断 0 和 12 是否在同一个集合内

🍅 代码实现
代码示例
// 判断操作(判断x1和x2是否在同一个集合内)
bool InSet(int x1, int x2)
{
// 直接返回结果即可
return FindRoot(x1) == FindRoot(x2);
}
🍑 集合个数
如何找到这个数组有多少个集合呢?
这个接口也很简单,我们只需要判断数组里面有几个负数,那么说明就有多少个集合,因为负数代表树的根节点。
🍅 代码实现
代码示例
// 集合个数(找到这个数组有多少个集合)
size_t SetSize()
{
size_t size = 0; // 统计集合的个数
for (size_t i = 0; i < _ufs.size(); ++i) // 遍历真个数组
{
if (_ufs[i] < 0) // 如果i下标存储的元素小于0,说明就是一集合
{
++size; // 个数加1
}
}
return size; // 返回集合的个数
}
3. 并查集路径压缩
首先,让我们来回忆一下 FindRoot 执行的操作:从一个节点,不停的通过 parent 数组向上去寻找它的根节点,在这个过程中,我们相当于把从这个节点到根节点的这条路径上的所有的节点都给遍历了一遍,那么,思考一下,在 FindRoot 的同时,是否可以顺便加上一些其它的操作使得树的层数尽量变得更少呢?答案是可以的。
对于一个集合树来说,它的根节点下面可以依附着许多的节点,因此,我们可以尝试在 FindRoot 的过程中,从底向上,如果此时访问的节点不是根节点的话,那么我们可以把这个节点尽量的往上挪一挪,减少数的层数,这个过程就叫做路径压缩。
🍑 举例说明
下面举一个具体的例子来说明一下。
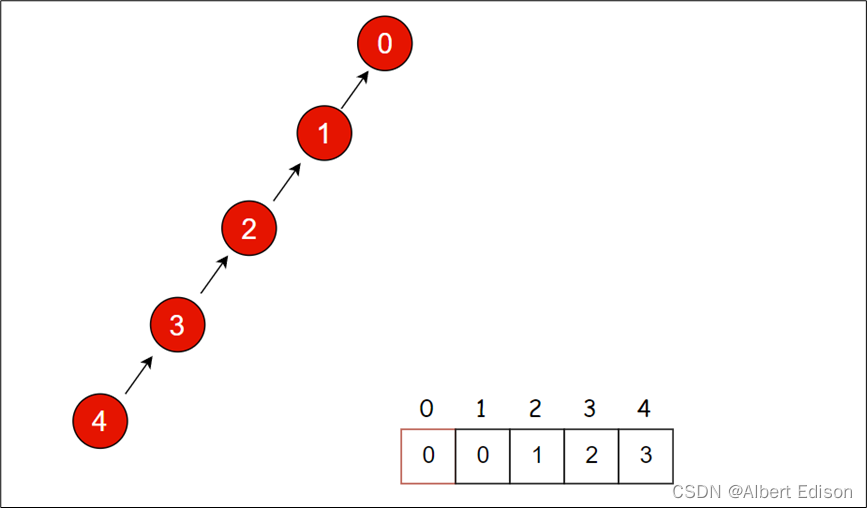
假设我们起始的并查集如上图所示,现在我们要 find[4],首先我们根据 parent[4] 可以得出,4 并不是一个根节点,因此,我们可以在向上继续查询之前,把这个节点往上面挪一挪(路径压缩),首先把 4 节点连接到其父亲 3 节点上,我们可以让 4 节点不在指向 3 节点作为父亲节点了,而是让其跳一下,让其指向 2 节点(即父亲节点的父亲节点)作为新的父亲节点:
- 如果该元素的父亲节点正好是根节点,那么让其指向父亲节点的父亲节点并不会出错,因为根据根元素的父亲节点指向其自己的结构,此时父亲节点的父亲节点仍然是有效的,即还是根节点,不会发生越界问题。
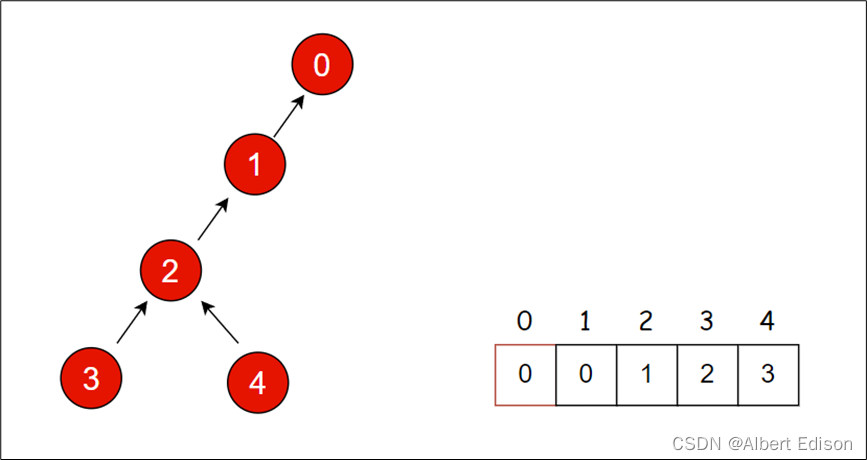
这样,我们就发现树的层数由原来的 5 层变成了现在的 4 层,即路径被压缩了一下。
下面,我们把继续来对 2 节点进行 find 操作,这里我们没有再去访问 3 节点,相当于跳过了一步操作(因为 3 节点也不是根节点,并不是我们想要返回的结果。如果 3 节点是根节点的话,那么 4 节点就会指向 3 节点,接下来就会访问 3 节点,所以这样的跳过是可行的),对于 2 节点来说,2 节点也不是我们所要找到的根节点,因此,我们同样也可以对其进行压缩操作,让 2 节点指向父亲节点的父亲节点 0 节点作为新的父亲节点,如下图所示:
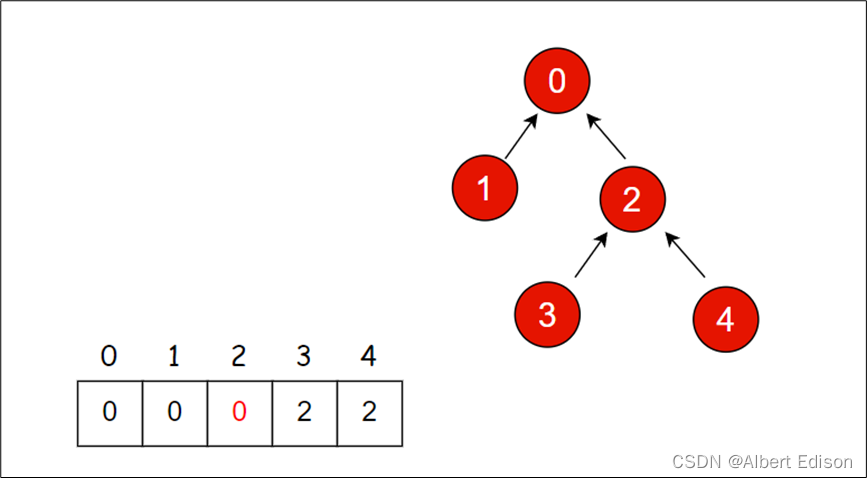
此时,树的层数由 4 层被压缩到了 3 层,与此同时,我们还跳过了一个 1 节点,接下来,我们只需要对 0 节点在进行路径压缩操作就好了。因为 0 节点是我们要找的根节点,因此,我们不在需要执行路径压缩操作了,只需要把找到的结果即根节点给返回就好了。
通过上面的过程我们可以看到,在进行 find 操作的同时,我们不仅把需要查找的根节点给找到了,与此同时我们还对树进行了压缩操作,这便是路径压缩的意思。通过路径压缩,我们在下一次执行 find 操作的时候,层数变得尽可能少了,那么效率将会大大的提高。
🍅 动图演示
现在我们要查找 8 的根节点,可以看到,当找到根节点以后,就把这条路径上的所有结点都连接到了根节点下面,从而进行了路径压缩

🍅 代码实现
代码示例
// 查询操作(路径压缩)
size_t FindRoot(int x)
{
// 先找到x的根节点节点
int root = x;
while (_ufs[root] >= 0)
root = _ufs[root];
// 路径压缩
// 从上面查找x根节点的路径开始更新
while (_ufs[x] >= 0) // 直到更新到 根节点!
{
//记录x的parnet,避免被修改
int parent = _ufs[x];
//直接让x作为root的子节点
_ufs[x] = root;
x = parent;
}
return x;
}
4. 并查集应用
🍅 省份数量
题目描述
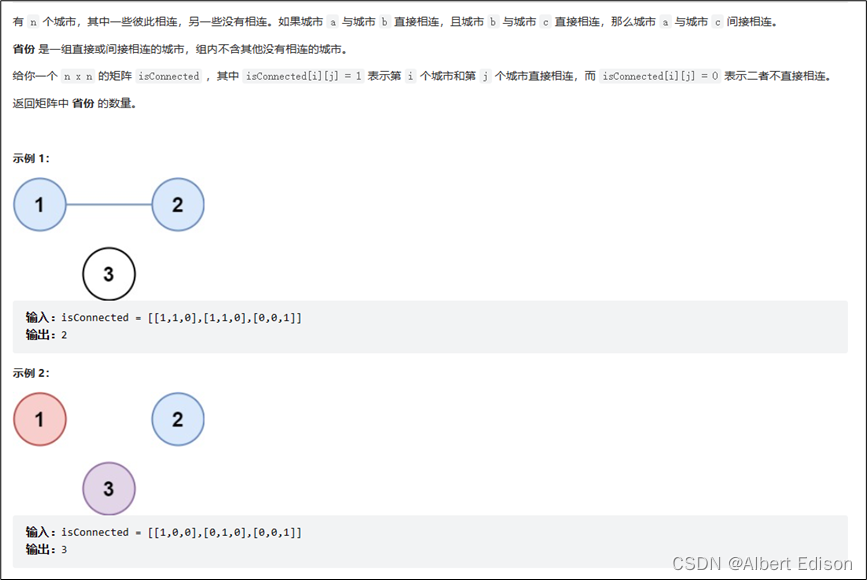
解题思路
- 写一个并查集
- 然后判断
isConnected[i][j]是否等于 1,如果等于 1,就放进一个集合中 - 最好返回并查集中的集合个数
代码实现
// 并查集
class UnionFindSet
{
public:
// 构造函数
UnionFindSet(size_t n)
:_ufs(n, -1)
{}
// 查询操作(找到x所在树的根节点)
int FindRoot(int x)
{
int parent = x; // x下标存储的值是它父亲的下标
while (_ufs[parent] >= 0) // 当父亲位置的值大于等于0,进入循环
{
parent = _ufs[parent];
}
// 程序走到这里,说明父亲位置里面存的是一个负数,即x的根节点
return parent;
}
// 合并操作(合并x1和x2)
void Union(int x1, int x2)
{
int root1 = FindRoot(x1); // 找到x1的根节点
int root2 = FindRoot(x2); // 找到x2的根节点
// 如果root1和root2相等,说明它俩本身就是在一个集合,那么就没必要合并了
if (root1 == root2)
return;
// 把小的根节点合并到大的根节点里面去
// 默认root2大,root1小
if (root1 > root2) // 如果root1大,root2小
swap(root1, root2); // 那么就交换
_ufs[root1] += _ufs[root2]; // 把root2所在树的节点个数添加到root1里面去
_ufs[root2] = root1; // root2位置存在的根节点为root1
}
// 判断操作(判断x1和x2是否在同一个集合内)
bool InSet(int x1, int x2)
{
// 直接返回结果即可
return FindRoot(x1) == FindRoot(x2);
}
// 集合个数(找到这个数组有多少个集合)
size_t SetSize()
{
size_t size = 0; // 统计集合的个数
for (size_t i = 0; i < _ufs.size(); ++i) // 遍历真个数组
{
if (_ufs[i] < 0) // 如果i下标存储的元素小于0,说明就是一集合
{
++size; // 个数加1
}
}
return size; // 返回集合的个数
}
private:
vector<int> _ufs; // 数组
};
// 省份相连
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
UnionFindSet ufs(isConnected.size());
for (size_t i = 0; i < isConnected.size(); ++i)
{
for (size_t j = 0; j < isConnected.size(); ++j)
{
// 如果i和j相连的话,就合并到一个集合中去
if (isConnected[i][j] == 1)
{
ufs.Union(i, j);
}
}
}
return ufs.SetSize();
}
};
其实也可以不用手撕一个并查集。
代码优化
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
// 手动控制并查集
vector<int> ufs(isConnected.size(), -1);
// 查找根
auto findRoot = [&ufs](int x)
{
while (ufs[x] >= 0)
{
x = ufs[x];
}
return x;
};
//
for (size_t i = 0; i < isConnected.size(); ++i)
{
for (size_t j = 0; j < isConnected[i].size(); ++j)
{
if (isConnected[i][j] == 1)
{
// 合并集合
int root1 = findRoot(i);
int root2 = findRoot(j);
if (root1 != root2)
{
ufs[root1] += ufs[root2];
ufs[root2] = root1;
}
}
}
}
//
int n = 0;
for (auto e : ufs)
{
if (e < 0)
{
++n;
}
}
//
return n;
}
};

![String类 [下]](https://img-blog.csdnimg.cn/0e589f1adfe3467d8fbf25b9bded99dc.png)