目录
1简介
2距离函数
2.1 L2范数(欧氏距离)
1简介
在数据科学中,相似性度量是一种衡量数据样本如何相互关联或相互接近的方法。另一方面,相异性度量是告诉数据对象有多少是不同的。此外,当相似的数据样本被分组到一个集群中时,这些术语通常用于聚类。所有其他数据样本被分组到不同的样本中。它还用于分类(例如 KNN),其中根据特征的相似性标记数据对象。另一个例子是当我们谈论与其他数据样本相比不同的异常值时(例如,异常检测)。
相似性度量通常表示为一个数值:当数据样本越相似时它就越高。它通常通过转换表示为零和一之间的数字:零表示相似度低(数据对象不相似)。一是相似度高(数据对象非常相似)。
让我们举一个例子,其中每个数据点只包含一个输入特征。这可以被认为是显示三个数据点 A、B 和 C 之间差异性的最简单示例。每个数据样本可以在一个轴上具有单个值(因为我们只有一个输入特征);让我们将其表示为 x 轴。让我们取两个点,A(0.5)、B(1) 和 C(30)。如您所知,与 C 相比,A 和 B 彼此足够接近。因此,A 和 B 之间的相似性高于 A 和 C 或 B 和 C。换句话说,A 和 B 具有很强的相关性。因此,距离越小,相似度越大。
当且仅当它满足以下四个条件时,给定的距离(例如相异性)才能成为度量:
1- 非负性:对于任意两个不同的观察值 p 和 q,d(p, q) ≥ 0。
2- 对称性:对于所有 p 和 q,d(p, q) = d(q, p)。
3- 三角不等式:对于所有 p、q、r,d(p, q) ≤ d(p, r) + d(r, q)。
4-仅当 p = q 时 d(p, q) = 0。
距离度量是分类的基本原则,例如 k 最近邻的分类器算法,它测量给定数据样本之间的差异性。此外,选择距离度量会对分类器的性能产生很大影响。因此,计算对象之间距离的方式将对分类器算法的性能起着至关重要的作用。
2距离函数
用于测量距离的技术取决于您正在处理的特定情况。例如,在某些地区,欧几里得距离可能是最佳的并且对计算距离很有用。其他应用程序需要更复杂的方法来计算点之间的距离或余弦距离等观测值。以下列举的列表表示计算每对数据点之间距离的各种方法。
2.1 L2范数(欧氏距离)
用于数字属性或特征的最常见距离函数是欧几里德距离,其定义如下:
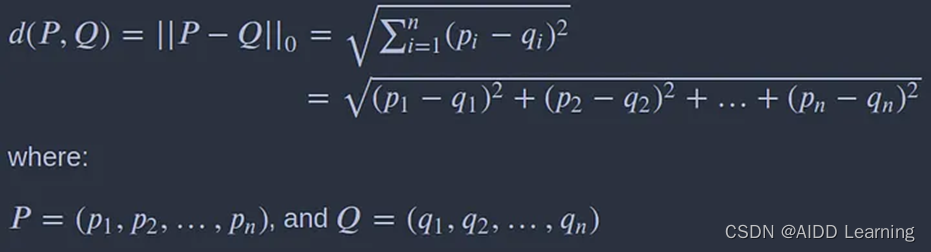
N维空间中两点之间的欧氏距离
距离度量具有众所周知的属性,例如对称、可微、凸、球形等。在二维空间中,等于直角三角形斜边的长度,上式公式可以表示为:

二维空间中两点之间的欧氏距离
此外,欧几里德距离是一种度量,因为它满足其标准,如下图所示。

欧氏距离满足作为度量的所有条件
此外,使用该公式计算的距离表示每对点之间的最小距离。也就是说,它是从A点到B点的最短路径(二维直角坐标系),如下图所示:
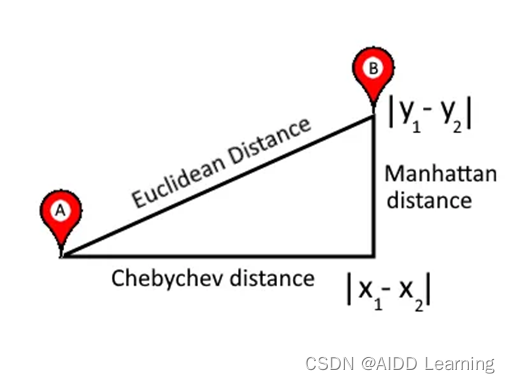
欧氏距离是最短路径(不包括量子世界中虫洞的情况)
因此,无论何时您想在路径上没有障碍物的情况下计算两点之间的距离,都可以使用此公式。相反,您想要使用其他度量标准,例如曼哈顿距离,这将在后期文章中进行解释。