欢迎关注更多精彩

问题描述

给定点O，线段AB，平面OP，求以OP法向为某一轴，以AB在OP上的投影为另一轴，O为原点的局部坐标系。要求给出X,Y,Z轴的单位向量，以及原点O. 求出转换到世界坐标系的旋转矩阵RT。

如图，

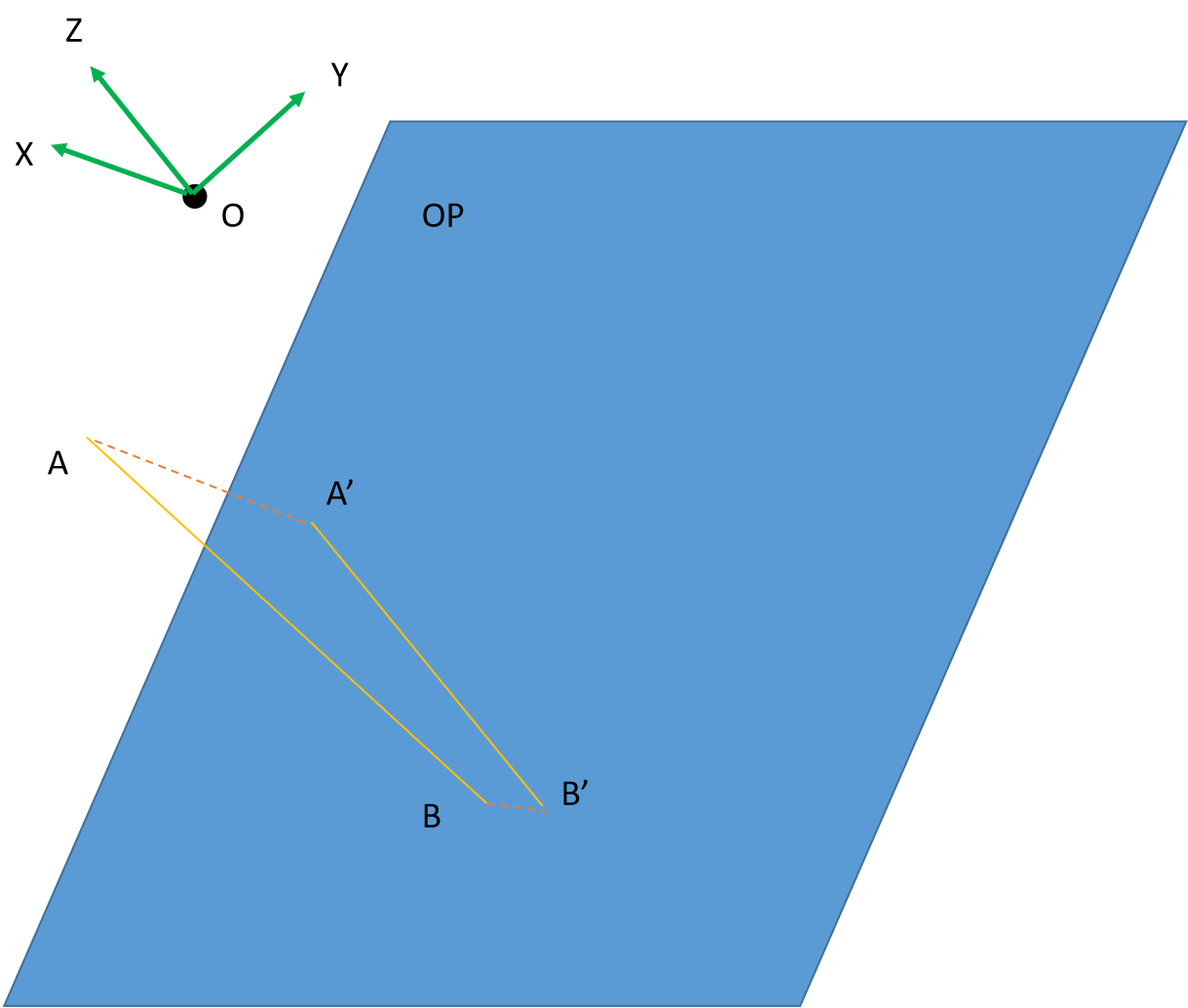
A’B’为AB在OP上的投影，坐标系中X轴平行于OP面的法向，Z轴平行于A’B’。

问题分析

关键技术难点

1. 投影的计算
2. 第三轴计算
3. 旋转矩阵计算

投影的计算

对线段的投影可以转化成两个端点的投影。
点的投影可以认识是由点出发沿平面法向的直线与平面的交点。
具体可以参考 点击前往

第三轴计算

条件中只给出两轴，必须计算第三轴。
由于三轴两两垂直，

根据公式

$Z=X\times Y，X=Y\times Z，Y=Z\times X$

可以发现，只要给定其中两轴必定可以计算出第三轴。

旋转矩阵计算

要求返回一个形如 点击前往的旋转矩阵。

基本思路是行把原点移动到（0，0，0）点RT1，然后先把X轴旋转到重合RT2，再把Y轴旋转到重合RT3。最终结果就是RT3*RT2*RT1。

接口设计&基本步骤

坐标系计算

接口设计

接口函数：

RigidRTMatrix GenerateCoordinate(const Point & p, const Point &line_start, 
const Point &line_end, const Point & plane_normal, const Point & plane_point, 
CoordinateOrient line_orient, CoordinateOrient normal_orient);

参数：
出参 RigidRTMatrix 矩阵的三行代表X,Y,Z坐标，Translation代表坐标系原点位置。

参数名	类型	作用	备注
p	行向量	坐标系原点
line_start	行向量	线段起点
line_end	行向量	线段终点
plane_normal	行向量	平面法向	单位向量
plane_point	行向量	平面上任意一点
line_orient	CoordinateOrient枚举形	线段投影指向代表的坐标系名称	X,Y,Z 可选
normal_orient	CoordinateOrient枚举形	线段投影指向代表的坐标系名称	X,Y,Z 可选

基本步骤

1.计算线段投影的单位向量。
2.根据输入要求确定坐标系的两个轴。
3.根据已经确定的两轴计算剩下的一轴。
4.确定原点。

旋转矩阵计算

接口设计

接口函数：

RigidRTMatrix Coordinate2RT(const RigidRTMatrix & coordinate);

参数：
出参 RigidRTMatrix，代表局部坐标系到世界坐标系的变换矩阵。

参数名	类型	作用	备注
coordinate	RigidRTMatrix	局部坐标系信息

基本步骤

1. 将坐标系原点移动致0点，矩阵为RTO
   
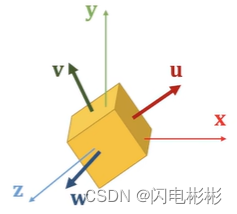
   设置新坐标系是uvw，原来是xyz。
   先计算矩阵A使得原坐标系转化到新坐标系。
   可以列出方程出
   $\{\begin{array}{l}A\cdot x=u\\ A\cdot y=v\\ A\cdot z=w\end{array}$
   u,v,w本身是正交的，且是单位向量。
   原来坐标系可以组成一个单位矩阵
   可以得到
   $A\cdot \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]=\left[\begin{array}{ccc}u& v& w\end{array}\right]$

$\therefore A=[uvw]$
最终结果为
$RT{O}^{-}1\ast A^T\ast RTO$

代码实现

• 代码库点击前往
• 代码库点击前往
• 代码库点击前往

坐标系计算

RigidRTMatrix GenerateCoordinate(const Point& p, const Point& line_start,
	const Point& line_end, const Point& plane_normal, const Point& plane_point,
	CoordinateOrient line_orient, CoordinateOrient normal_orient) {
	cout << "GenerateCoordinate" << endl;
	assert(abs(plane_normal.squaredNorm() - 1) < 1e-6);
	RigidRTMatrix coord;
	// 1.计算线段投影的单位向量。
	Point project_line_start = line_start;
	BasicTools::PointProjectPlane(project_line_start, plane_point, plane_normal);

	Point project_line_end = line_end;
	BasicTools::PointProjectPlane(project_line_end, plane_point, plane_normal);
	Point project_vec = (project_line_end - project_line_start).normalized();
	assert(project_vec.squaredNorm() > 1e-4);
	cout <<( project_vec.squaredNorm() > 1e-4) << endl;

	coord.mat.block<1, 3>(line_orient, 0) = project_vec;
	// 2.根据输入要求确定坐标系的两个轴。
	coord.mat.block<1, 3>(normal_orient, 0) = plane_normal;
	// 3.根据已经确定的两轴计算剩下的一轴。
	int left = CoordinateOrient::X + CoordinateOrient::Y + CoordinateOrient::Z;
	left -= line_orient + normal_orient;
	coord.mat.block<1, 3>(left, 0) = coord.mat.block<1, 3>((left + 1) % 3, 0).cross(coord.mat.block<1, 3>((left + 2) % 3, 0));

	// 4.确定原点。
	coord.trans = p;

	return coord;
}

旋转矩阵计算

RigidRTMatrix Coordinate2RT(const RigidRTMatrix& coord) {
	RigidRTMatrix res;
	RigidRTMatrix RTO;
	RTO.trans = -coord.trans;
	RigidRTMatrix RTOInvers;
	RTOInvers.trans = coord.trans;
	RigidRTMatrix A;
	A.mat = coord.mat.transpose();
	res = A * RTO;
	res = RTOInvers * res;
	return res;
}

---

本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。