---

子集问题

1 78 子集

如果把 子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题是收集树的叶子节点，而子集问题是找树的所有节点！

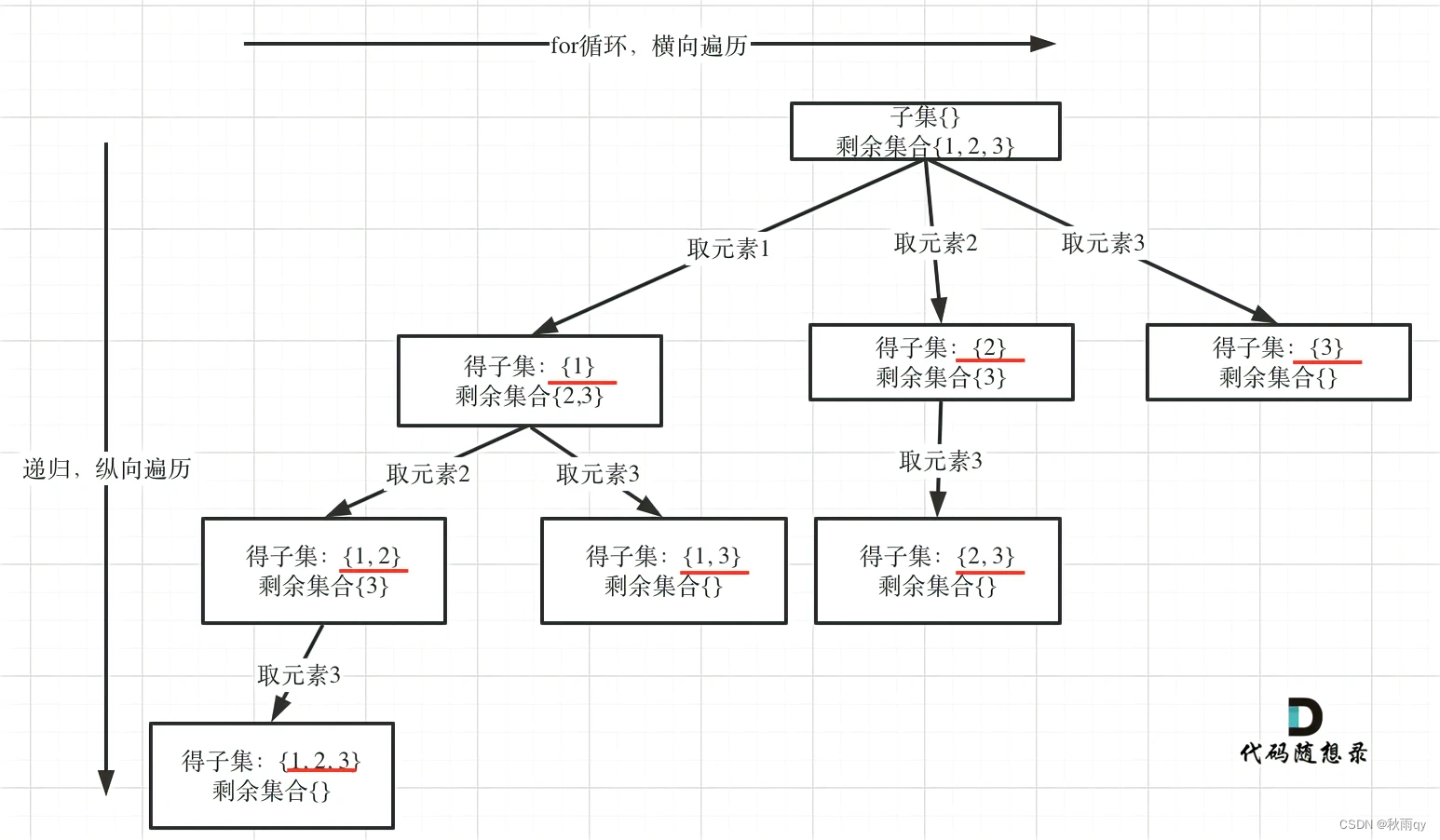
因为需要找到所有的节点，所以终止条件可以去掉。

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void dfs(vector<int>& nums, int startIndex){
        //if(startIndex == nums.size()){
        //    return;
        //}

        for(int i = startIndex; i < nums.size(); ++i){
            path.push_back(nums[i]);
            res.push_back(path);
            dfs(nums, i + 1);
            path.pop_back();
        }
    }

    vector<vector<int>> subsets(vector<int>& nums) {
        dfs(nums, 0);
        path.clear();
        res.push_back(path);
        return res;
    }
};

2 90 子集II

此题与题1不同之处在于，给定的nums数组中可能包含重复的元素。
作为子集问题同样无需return条件。

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void dfs(vector<int>& nums, int startIndex) {
        res.push_back(path);

        for(int i = startIndex; i < nums.size(); ++i) {
            if(i > startIndex && nums[i] == nums[i-1]){
                continue;
            }
            path.push_back(nums[i]);
            dfs(nums, i + 1);
            path.pop_back();
        }
    }

    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        dfs(nums, 0);
        return res;
    }
};

3 491 递增子序列

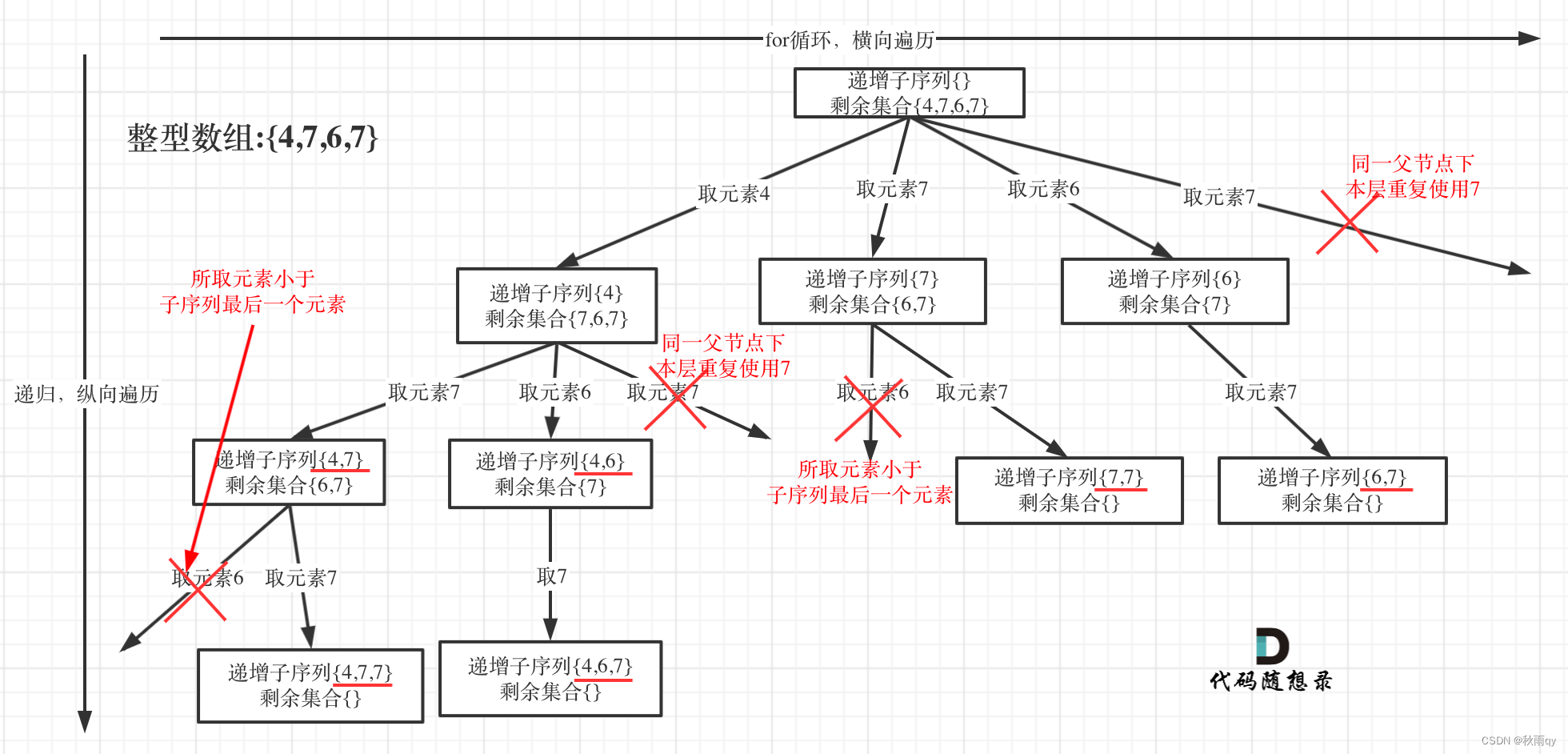
两个特点：
1、一个元素不能重复使用，所以需要startIndex。
2、数组中可能含有重复元素（但不能用之前的去重套路，因为不能对数组进行排序）。
故需要用哈希表进行去重。

unordered_set<int> uset; // 使用set来对本层元素进行去重
for (int i = startIndex; i < nums.size(); i++) {
    if ((!path.empty() && nums[i] < path.back())
            || uset.find(nums[i]) != uset.end()) {
            continue;
    }
    uset.insert(nums[i]); // 记录这个元素在本层用过了，本层后面不能再用了
    path.push_back(nums[i]);
    backtracking(nums, i + 1);
    path.pop_back();
}