一、本周周赛总结

• 干T2写wa了
• T1 模拟。
• T2 递推模拟。
• T3 DP或bfs。
• T4 图论并查集。
  

6430. 找出转圈游戏输家

6430. 找出转圈游戏输家

1. 题目描述

2. 思路分析

按题意模拟即可。

• 由于每个人只会接球一次，复杂度是n。

3. 代码实现

class Solution:
    def circularGameLosers(self, n: int, k: int) -> List[int]:
        vis = [0] * n
        x = 0
        cnt = 1
        while True:
            if vis[x]:break
            vis[x] = 1 
            x = (x+k*cnt)%n
            cnt += 1
        return [x+1 for x,v in enumerate(vis) if not v]

6431. 相邻值的按位异或

6431. 相邻值的按位异或

1. 题目描述

2. 思路分析

• 朴素思路是把第一位设置成1或0直接模拟到最后一位看看是否合法。
• 写完发现其实就是把所有位异或起来再异或s是否等于s。
• 那只有0异或别人是保持。

3. 代码实现

class Solution:        
    
    def doesValidArrayExist(self, derived: list[int]) -> bool:
        def check(s):
            t = s 
            for v in derived:
                t^=v
            return t == s

        return check(0) or check(1)

class Solution:            
    def doesValidArrayExist(self, derived: list[int]) -> bool:    
        return reduce(xor,derived)==0

6433. 矩阵中移动的最大次数

6433. 矩阵中移动的最大次数

1. 题目描述

2. 思路分析

• 转移时定向的，可以直接向右DP。

3. 代码实现

class Solution:
    def maxMoves(self, g: List[List[int]]) -> int:
        m,n = len(g),len(g[0])
        f = [[0]+[-inf]*(n-1) for _ in range(m)]
        ans = 0
        for j in range(1,n):
            for i in range(m):
                if g[i][j] > g[i][j-1]:
                    f[i][j] = max(f[i][j],f[i][j-1]+1)
                if i and g[i][j] > g[i-1][j-1]:
                    f[i][j] = max(f[i][j],f[i-1][j-1]+1)
                if i < m-1 and g[i][j] > g[i+1][j-1]:
                    f[i][j] = max(f[i][j],f[i+1][j-1]+1)
                ans = max(ans,f[i][j])
        return ans 

6432. 统计完全连通分量的数量

6432. 统计完全连通分量的数量

1. 题目描述

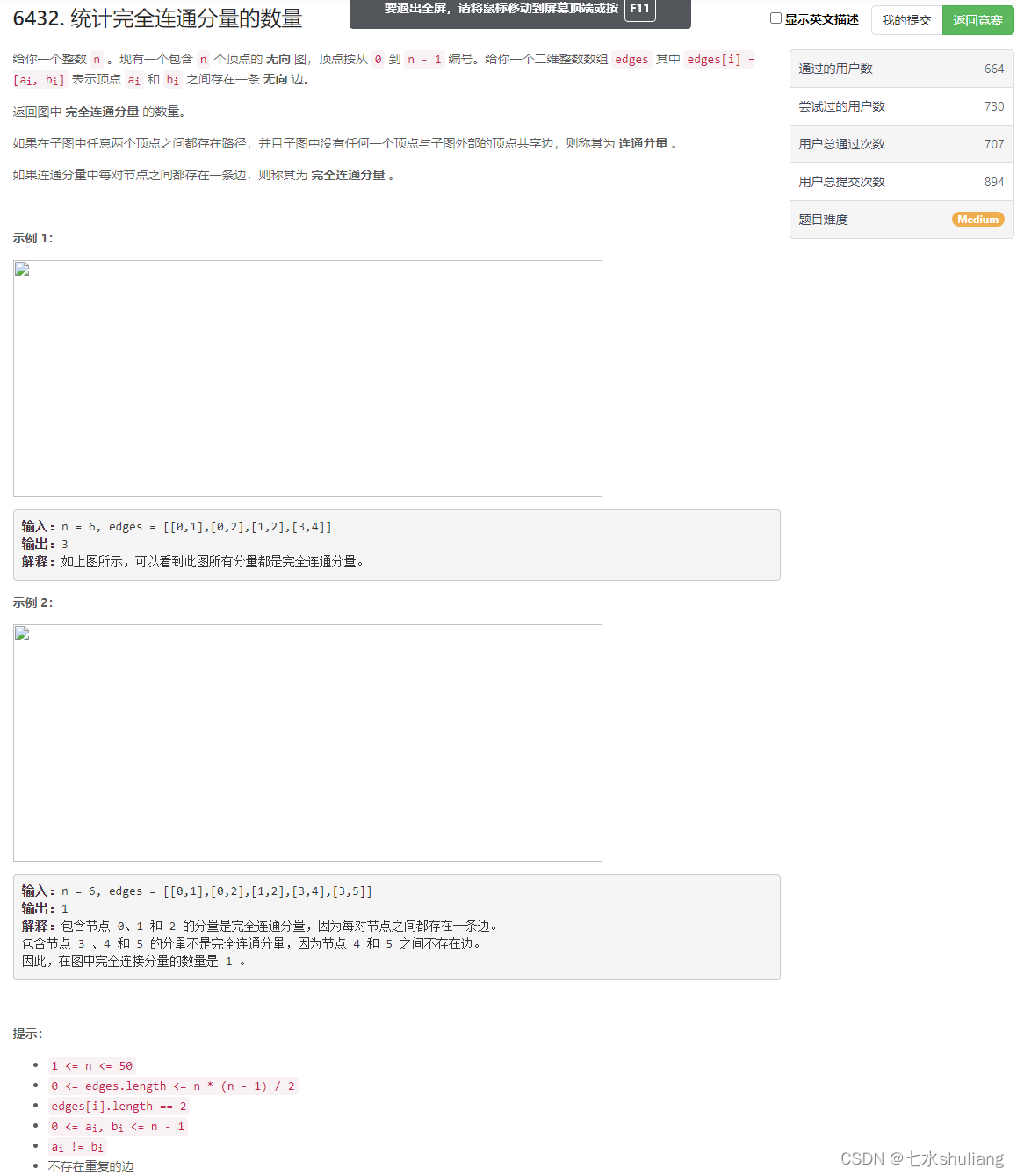
2. 思路分析

• 图是裂的，只好手画。好在题意说的比较明确。
• 求连通分量直接并查集即可，然后看每个分量的边数m和点数n的关系，对于完全连通分量，有：
  • m=n*(n-1)/2
• 前阵子正好写了维护边数的并查集。

3. 代码实现

class DSU:
    def __init__(self, n):
        self.fathers = list(range(n))
        self.size = [1] * n  # 本家族size
        self.edge_size = [0] * n  # 本家族边数(带自环/重边)
        self.n = n
        self.setCount = n  # 共几个家族

    def find_fa(self, x):
        fs = self.fathers
        t = x
        while fs[x] != x:
            x = fs[x]
        while t != x:
            fs[t], t = x, fs[t]
        return x

    def union(self, x: int, y: int) -> bool:
        x = self.find_fa(x)
        y = self.find_fa(y)

        if x == y:
            self.edge_size[y] += 1
            return False
        # if self.size[x] > self.size[y]:  # 注意如果要定向合并x->y，需要干掉这个；实际上上边改成find_fa后，按轶合并没必要了，所以可以常关
        #     x, y = y, x
        self.fathers[x] = y
        self.size[y] += self.size[x]
        self.edge_size[y] += 1 + self.edge_size[x]
        self.setCount -= 1
        return True
class Solution:
    def countCompleteComponents(self, n: int, edges: List[List[int]]) -> int:
        dsu = DSU(n)
        for u,v in edges:
            dsu.union(u,v)
        ans = 0
        
        for i in range(n):
            if dsu.find_fa(i) == i :
                p = dsu.size[i]
                m = dsu.edge_size[i]
                if p*(p-1)//2 == m:
                    ans +=1
        return ans         

参考链接