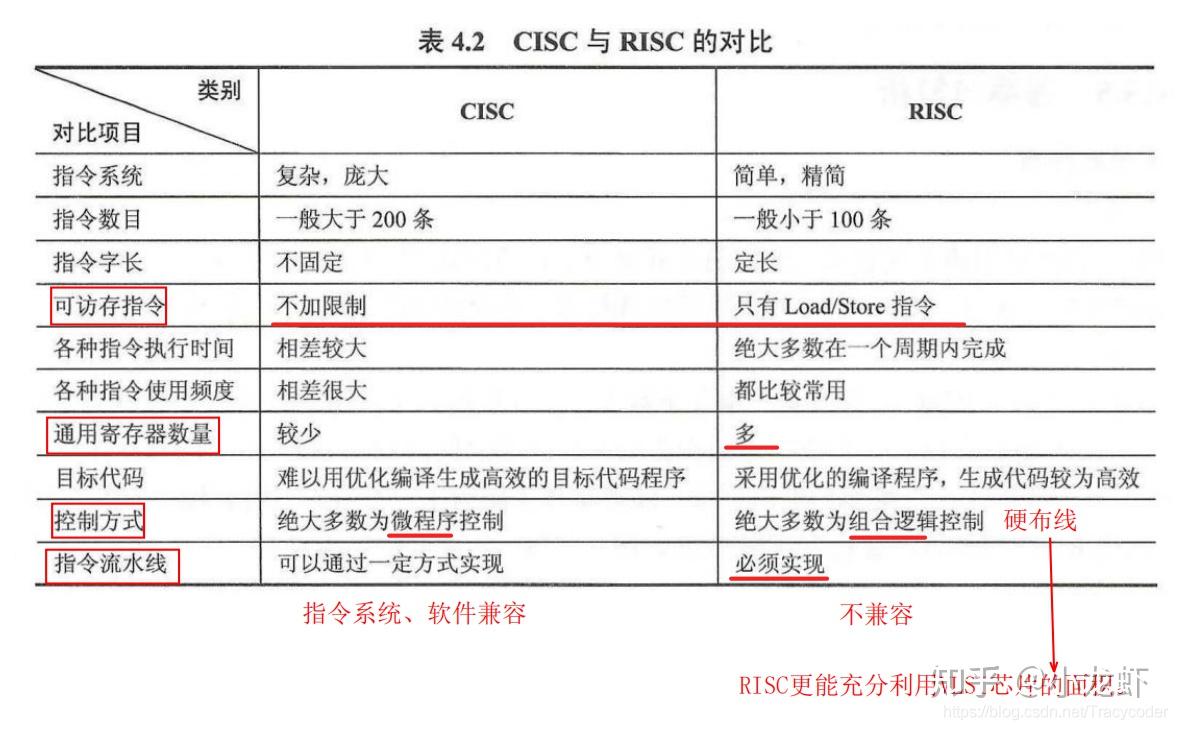
目录
- 1 引入情境
- 基本归并排序实现 C++
- 2 原地归并排序
- 2-1 死板的解法
- 2-2 原地工作区
- 2-3 链表归并排序
- 3 自底向上归并排序
- 4 两路自然归并排序
- 4-1 形式化描述
- 4-2 代码实现
1 引入情境
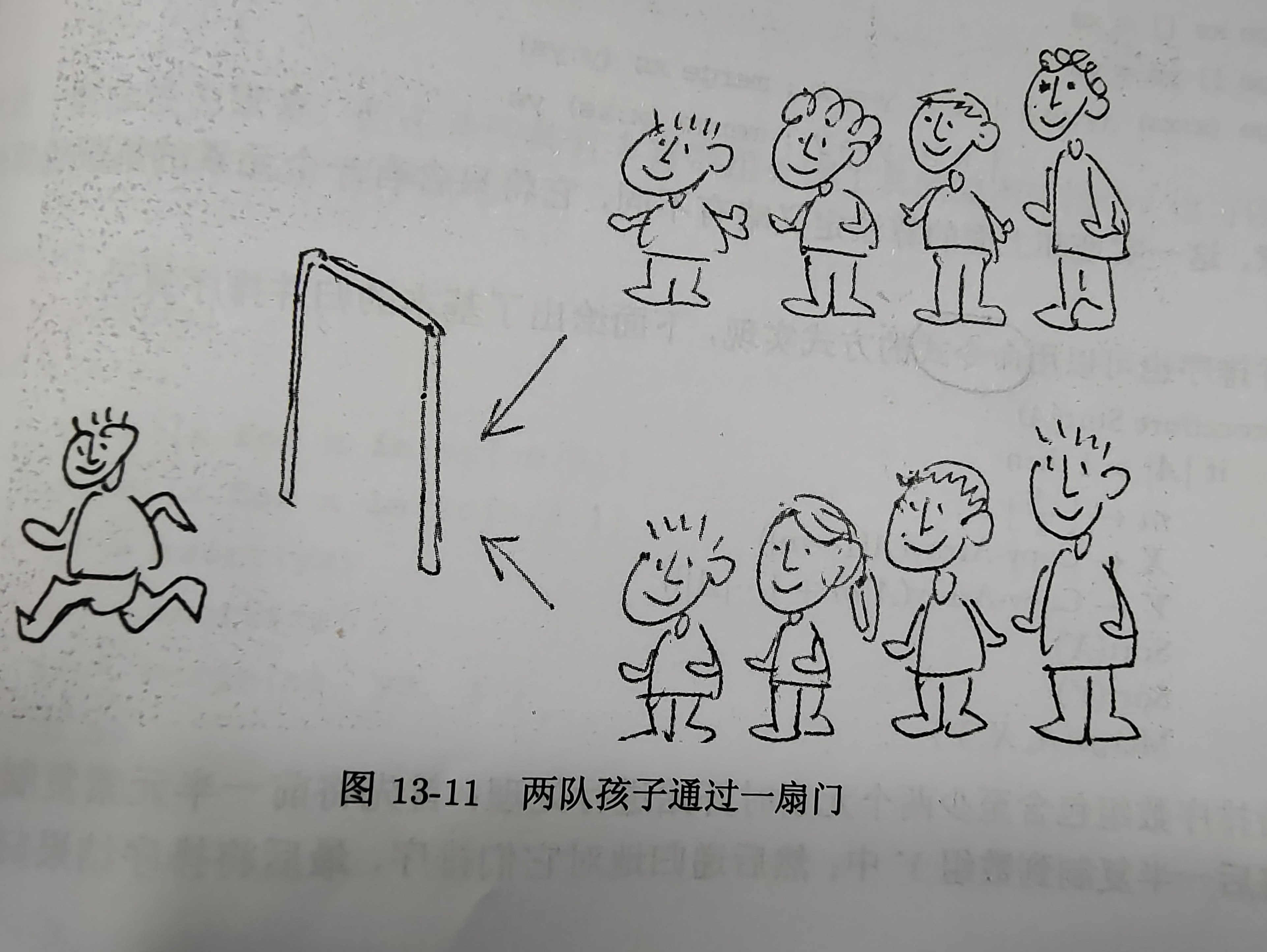
归并思想:假设有两队小孩,都是从矮到高排序,现在通过一扇门后合并为一队。要求:任何孩子,只有所有比它矮的孩子通过后,才能通过。
function merge_sort(A):
if len(A) > 1 then
m = floor(len(A)/2) # 获取中心点
X = copy_array(A,0,m)
Y = copy_array(A,m+1,len(A)-1) #拆成差不多的两半
merge_sort(X)
merge_sort(Y) # 分别排序
merge(A,X,Y) # 合并
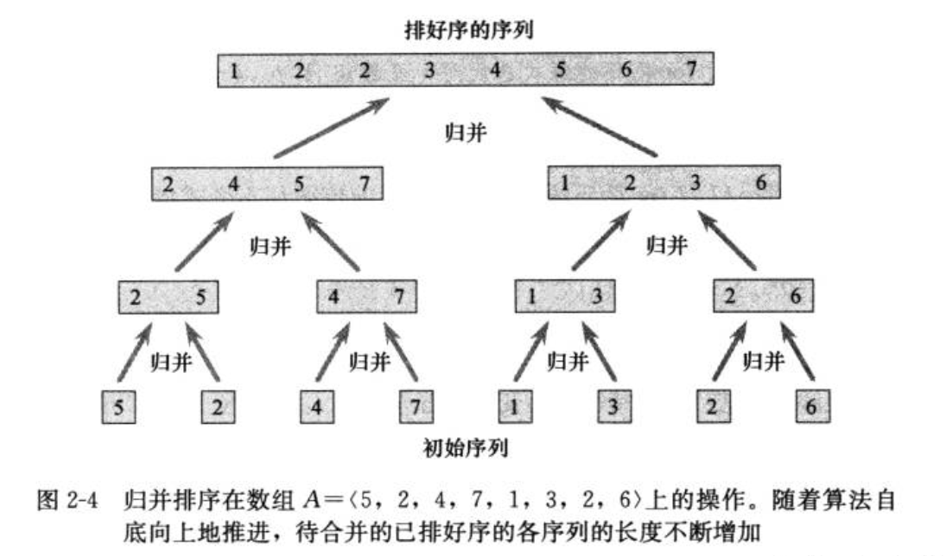
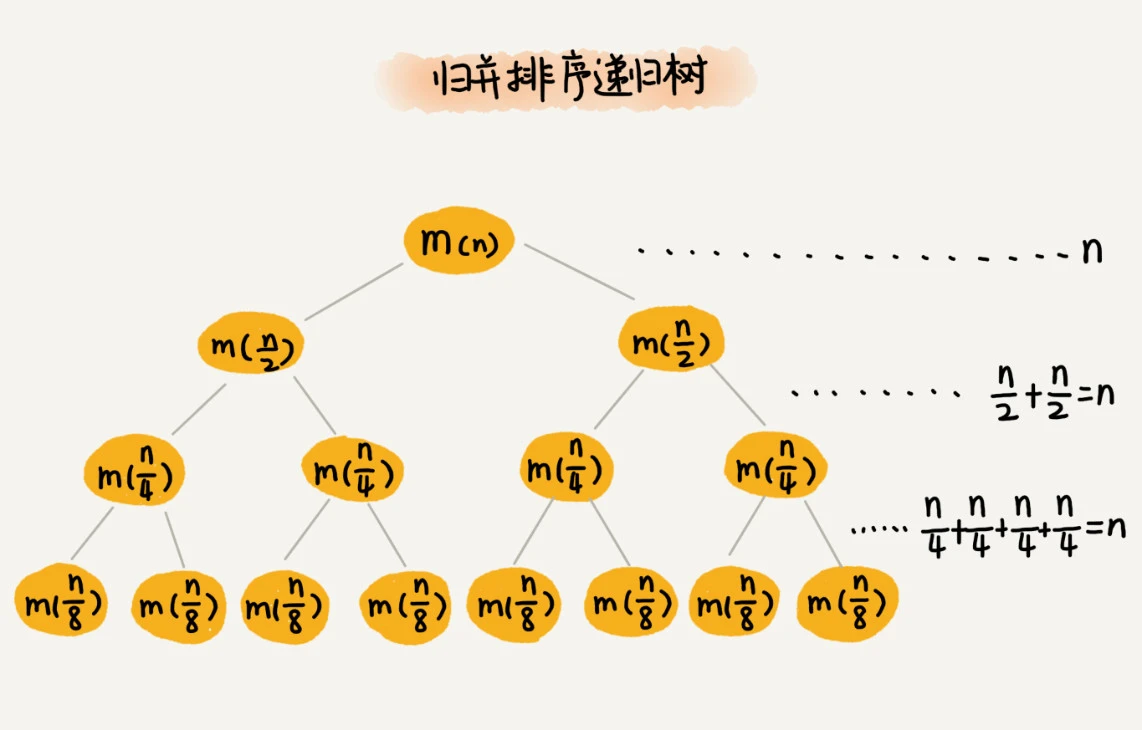
假如我理解了上面归并,但是,在排序之前,怎么得到有序的两个队列呢?注意到,伪代码的出口是 l e n ( A ) ≤ 1 len(A) \leq 1 len(A)≤1 就会返回,即一个数本身有序。当它拆分到自然有序,返回头开始合并,直接上图:
只剩下一个问题,merge(A,X,Y)是怎么做的?简单的理解,每次比较X,Y头部,选一个最小的放到目标有序数组A的队尾即可;若一队为空,另一队还有剩余就直接放到A的队尾。给出伪代码描述:
function Merge(A,X,Y):
i=1,j=1,k=1
xlen=|X|
ylen=|Y|
# 从队伍头部选一个最小的放到目标队伍末尾
while i<= xlen and j <=ylen do
if X[i] <= Y[i] then
A[k] = X[i]
i = i + 1
else
A[k] = Y[j]
j = j + 1
k = k + 1
# 处理剩余的部分,放到末尾
while i <= xlen do
A[k] = X[i]
k = k + 1
while j <= ylen do
A[k]= Y[j]
j = j + 1
关于时间复杂度,设排序用时为
T
(
N
)
T(N)
T(N),则递归开销为:
T
(
N
)
=
T
(
N
2
)
+
T
(
N
2
)
+
c
N
T(N) = T(\frac {N} {2})+T(\frac {N} {2})+cN
T(N)=T(2N)+T(2N)+cN
对两半分别排序是
2
T
(
N
2
)
2T(\frac {N} {2})
2T(2N),
c
n
cn
cn是合并两个队列用时,解开后是O(NlgN)。另一种直观理解的方式如下图,拆半分层最多是
l
g
N
lgN
lgN层,每层归并都是O(N),相乘即可。
基本归并排序实现 C++
在实现之前,我们加一个小改进,在每队队伍加入一个哨兵:正无穷大(如果是非递增是负无穷),于是,merge的过程无需另行考虑剩余部分。
# 加入正无穷哨兵,会让一个较短的队列的下标阻塞在末尾
function merge(A,X,Y):
append(X,INF) # 在队列尾加入哨兵,正无穷INF
append(Y,INF)
for k from 1 to A.len do
if X[i] < Y[j] then
A[k]=X[i]
i = i + 1
else
A[k]=Y[j]
j =j + 1
实现时发生了两个错误:
l+(r-l)>>1和l+(r-l)/2是不同的;l+(r-l)/2和l+((r-l)>>1)才等价- l 和 1 总是容易弄混;下载编程字体点链接source code Pro
#include <iostream>
#include <vector>
#include <string>
using namespace std;
const int INF=1e5;
using Key=int;
using Array =vector<Key>;
void merge(Array &A,int l,int m,int r){
// 开两个队列分别放 A[l,m) A[m,r)
Array X(m-l+1);//多一个哨兵的位置
Array Y(r-m+1);
//复制元素
int i=0,j=0;
for(int k=l;k<m;++k) X[i++]=A[k];
for(int k=m;k<r;++k) Y[j++]=A[k];
X[m-l]=INF; //设置哨兵
Y[r-m]=INF;
for(i=0,j=0;l<r;++l){
A[l]=X[i] < Y[j] ? X[i++]:Y[j++];
}
}
// A[l,r)
void merge_sort(Array &A,int l,int r){
if(r-l>1){
int m = l+(r-l)/2; // 防止溢出
merge_sort(A,l,m);
merge_sort(A,m,r);
merge(A,l,m,r);
}
}
static void see_array(string arr_info,const Array &A){
cout<<arr_info <<" { ";
for(auto& item:A){
cout<<item<<" ";
}
cout<<"}"<<endl;
}
void test(){
Array arr{23,45,1,2,7,5,6};
// merge(arr,0,3,arr.size());
merge_sort(arr,0,arr.size());
see_array("sorted ",arr);
}
int main()
{
test();
return 0;
}
注意到,在merge中需要申请两个数组来放数据,频繁的申请释放内存会花费大量的时间。一个解决办法是一次性申请一个和待排序数组一样大的数组B,作为工作区。这一改进将所需空间从O(NLgN)减少到了O(N),对十万个数字排序上速度提示20%~25%。C++实现如下:
#include <iostream>
#include <vector>
#include <string>
using namespace std;
const int INF=1e5;
using Key=int;
using Array =vector<Key>;
void merge(Array &A,Array &B,int l,int m,int r){
// 合并 A[l,m) A[m,r) 到 B,再复制回来
int i,j,k;
// 记录两个队列的起点
i=k=l;
j=m;
// 归并
while(i<m && j<r){
B[k++]=A[i]<A[j] ? A[i++]:A[j++];
}
// 收尾工作
while(i<m) B[k++]=A[i++];
while(j<r) B[k++]=A[j++];
for(;l<r;++l) A[l]=B[l];
}
void msort(Array &A,Array &B,int l,int r){
int m;
if(r-l>1){
m = l+(r-l)/2; // 防止溢出
msort(A,B,l,m);
msort(A,B,m,r);
merge(A,B,l,m,r);
}
}
// A[l,r)
void merge_sort(Array &A,int l,int r){
Array B(r-l); //申请一个同样大小的工作区
msort(A,B,l,r);
}
static void see_array(string arr_info,const Array &A){
cout<<arr_info <<" { ";
for(auto& item:A){
cout<<item<<" ";
}
cout<<"}"<<endl;
}
void test(){
Array arr{23,45,1,2,7,5,6};
// merge(arr,0,3,arr.size());
merge_sort(arr,0,arr.size());
see_array("sorted ",arr);
}
int main()
{
test();
return 0;
}
2 原地归并排序
不带优化的基本实现需要空间O(NLgN),使用工作区也需要O(N),可以不用额外空间原地排序吗?
2-1 死板的解法
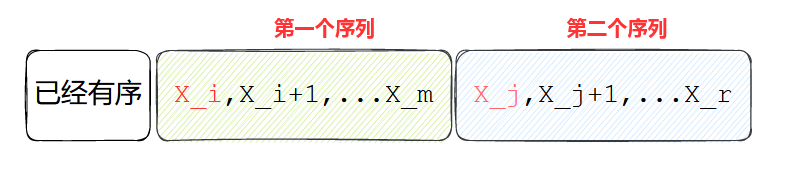
如下图,类比插入排序,通过比较 x i x_i xi和 x j x_j xj的大小确定把谁放在当前 x i x_i xi的位置上;注意到如果 x j x_j xj是更小的那个,需要把第一个序列整体向后移动一步,即覆盖掉 x j x_j xj,这样一来归并排序降低为 O ( N 2 ) O(N^2) O(N2)。
void naive_merge(Array &A,int l,int m,int r){
int i;
Key tmp;
for(;l<m && m<r;++l){
if(!(A[l]<A[m])){
tmp=A[m++]; //先保存,后覆盖
for(i=m-1;i>l;--i) A[i]=A[i-1];
A[l]=tmp;
}
}
}
2-2 原地工作区
注意,这一节有亿点点的抽象,看不懂可以跳过。原地工作区的思路是借用数组未排序的部分复用为归并的工作区,稍作思考就会发现有几个问题:
-
工作区一般是空白的,如果和未排序元素共用,会不会直接把原来的、还没有排序的数据给覆盖,造成数据丢失?
-
有序的子序列很大,自然意味着剩余未排序的空间小,那用这么小的工作区能完成归并任务吗?是不是和有序的子数组也会重叠呢?
先记下这些问题并直接给出方案,并逐渐改进使问题得到应对。
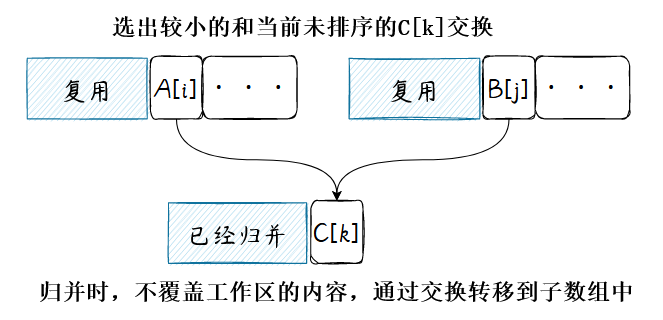
核心操作就是交换未排序的数据到子序列中,伪代码描述:
function merge(A,[i,m),[j,n),k):
while i<m and j <n do
if A[i]<A[j] then
swap(A[k],A[i])
i =i+1
else
swap(A[k],A[j])
j =j+1
k=k+1
while i<m do
swap(A[k],A[i])
i=i+1
k=k+1
while j<n do
swap(A[k],A[j])
j=j+1
k=k+1
考虑问题2,在工作区>=待归并元素长的条件下,容易实现数组的一半有序,因为可以拿另一半作为工作区。接下来的问题是,剩下的一半怎么搞?再递归呢?如果直接归并1/4和1/2,未排序的复用空间明显不够用。
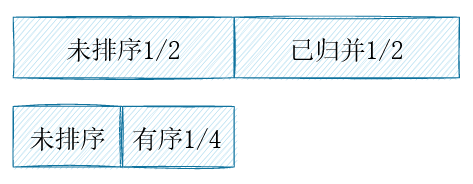
实际上,工作区可以和任何一个有序的子数组重叠,但是需要保证,尚未归并的元素不会被覆盖。所以,当归并1/4和1/2的元素时,我们可以把工作区放在正中间,允许它和有序的子数组重叠。
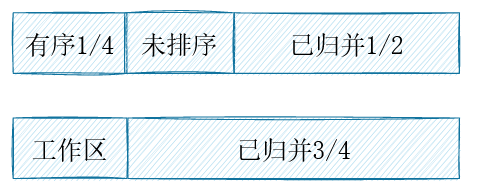
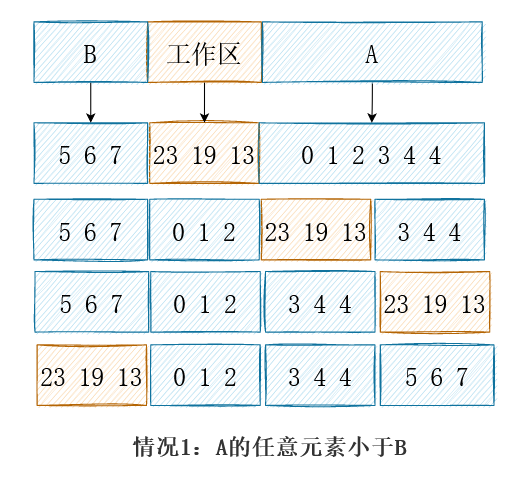
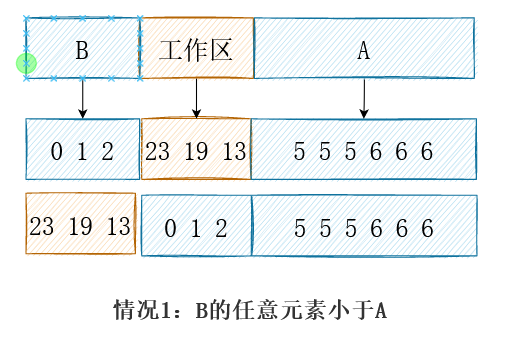
其他正常的例子与特殊情况均可保证工作区被换到左侧。于是算法明确了:总是重复对未排序部分的前1/2进行排序,从而将有序的结果交换到前一半,而使得工作区位于中间。渐渐当工作区足够小,剩余一个元素等价于插入排序;实际上对于最后几个元素(20以内)完全可以直接插入排序。伪代码描述如下:
function sort(A,l,r)
if r-l>0 then
m = floor((l+r)/2)
w = l+r-m # 工作区的起点
sort1(A,l,m,w) # 保证后一半元素有序
while w -l >1 do # 工作区间不为空
nr = w
w = ceil((l+nr)/2)
sort1(A,w,nr,l) # 同样递归对后1/2排序后放到前面
merge(A,[l,l+nr-w],[nr,r],w)
## 改用插入排序
for i from w down-to l do
j =i
while j <= r and A[j]<A[j-1] do
swap(A[j],A[j-1])
j=j+1
#反向调用sort 用于交换工作区和有序部分
function sort1(A,l,r,w)
if r-l > 0 then
m = floor((l+r)/2)
sort(A,l,m)
sort(A,m+1,r)
merge(A,[l,m],[m+1,r],w) #排序并放到w开始的位置
else #将所有元素交换到工作区
while l<=r do
swap(A[l],A[w])
l =l+1
w =w+1
注意虽然实现了原地归并,即O(1)的空间复杂度,但多了不少额外的交换操作。和使用额外工作区的版本相比,对十万个数字排序,速度下降了60%。C++ 详细实现如下:
#include <iostream>
#include <cmath>
#include <ctime> //随机数组
using namespace std;
using Key = int;
// 定于一个区间
struct Range
{
int l, r;
Range(int a, int b) : l(a), r(b) {}
void set(int left, int right)
{
l = left;
r = right;
}
int size()
{
return r - l;
}
}; //[l,r);
// 封装C语言的数组
struct Array
{
Key *arr;
int len;
Array(int l) : len(l)
{
arr = (Key *)malloc(sizeof(Key) * len);
srand(time(NULL));
static const int M=15; //在1~M范围内生成随机数
for (int i = 0; i < len; i++)
{
at(i) = rand() % M + 1;
}
}
Key &operator[](int i)
{
return *(arr + i);
}
Key &at(int i)
{
return *(arr + i);
}
void swap(int i, int j)
{
Key tmp = at(i);
at(i) = at(j);
at(j) = tmp;
}
void exchange(Array &B)
{
Key *tmp = arr;
arr = B.arr;
B.arr = tmp;
}
void show(const char info[]=""){
cout<<info<<"[";
for (size_t i = 0; i < len; i++)
{
cout<<at(i)<<" ";
}
cout<<"]."<<endl;
}
};
/// @brief 将数组A的两个区间的内容归并到start开始的区域
/// @param A 原数组
/// @param X 原数组的一个区间
/// @param Y 另一个区间
/// @param start 存放归并结果的开始位置
void merge(Array &A, Range &X, Range &Y, int start)
{
while (X.l < X.r && Y.l < Y.r)
{
int now = A[X.l] < A[Y.l] ? X.l++ : Y.l++;
A.swap(start++, now);
}
while (X.l < X.r)
A.swap(start++, X.l++);
while (Y.l < Y.r)
A.swap(start++, Y.l++);
}
void sort(Array &A, int l, int r, int w);
void merge_sort(Array &A, int l, int r)
{
int m, n, w;
if (r - l > 1)
{
m = l + (r - l) / 2; // mid
w = l + r - m; // 工作区的终点+1
sort(A, l, m, w); // 将前一半排序放到后一半
//[l,w]当前待排序的区间
while (w - l > 2)
{
n = w;
w = l + (n - l + 1) / 2;
sort(A, w, n, l); // 排序后一半放到前面
Range X(l, l + n - w), Y(n, r);
merge(A, X, Y, w); // 将两头有序数组合并
}
// 剩下一两个数作插入排序
for (n = w; n >= l; --n)
{
for (m = n; m < r && A[m] < A[m - 1]; ++m)
{
A.swap(m, m - 1);
}
}
}
}
/// @brief 把A[l,r)排序后,放到从下标w开始的区域
void sort(Array &A, int l, int r, int w)
{
int m;
if (r - l > 1)
{
m = l + (r - l) / 2;
merge_sort(A, l, m);
merge_sort(A, m, r);
Range X(l, m), Y(m, r);
merge(A, X, Y, w);
}
else
{
while (l < r)
{
A.swap(l++, w++);
}
}
}
void test()
{
int len = 8;
Array A(len);
A.show("srcArr ");
// test sort
// sort(A,0,3,3);
merge_sort(A, 0, len);
A.show("sorted ");
}
int main()
{
test();
return 0;
}
2-3 链表归并排序
和数组存储类似,链表也需要均分为两个差不多长的子序列,这里使用一种奇偶分割法,简单说,从原链表头部摘下节点,交替放到两个不同的子链表中。伪代码说明:
function split(L):
(A,B) =(null,null)
while L not null do
ptr = L # 当前头结点
L = next(L) # 头指针后移
A = link(p,A) #将p放到链表A的头部
swap(A,B) # 交换,下次换B被插入新元素
return (A,B)
C++ 详细实现如下:
#include <iostream>
#include <vector>
#include <string>
using namespace std;
const int INF=1e5;
using Key=int;
using Array =vector<Key>;
struct Node{
Key val;
struct Node* nxt;
Node(Key k,struct Node* next=nullptr):val(k),nxt(next){}
};
using Nptr=struct Node* ;
Nptr link(Nptr pre,Nptr old_head){
pre->nxt=old_head;
return pre;
}
Nptr mk_list(const Array &A){
Nptr head=new Node(-1);
Nptr p=head;
for(auto &x:A){
Nptr now=new Node(x);
p->nxt=now;
p=now;
}
return head->nxt;
}
Nptr merge(Nptr ap,Nptr bp){
Nptr head=new Node(-1);//哨兵,头结点
Nptr p=head;
while(ap && bp){
if(ap->val<bp->val){
link(p,ap);
ap=ap->nxt;
}else{
link(p,bp);
bp=bp->nxt;
}
p=p->nxt;
}
if(ap) link(p,ap);
if(bp) link(p,bp);
return head->nxt;
}
Nptr msort(Nptr L){
Nptr p, ap,bp;
if(!L || !L->nxt) return L;
ap=bp=nullptr;
while(L){
p=L;
L=L->nxt;
ap=link(p,ap);
swap(ap,bp);
}
ap=msort(ap);
bp=msort(bp);
return merge(ap,bp);
}
void test_list(){
Array A{23,7,1,56,23,8,31};
Nptr l=mk_list(A);
l=msort(l);
Nptr p=l;
while(p){
cout<<p->val<<endl;
p=p->nxt;
}
}
int main()
{
test_list();
return 0;
}
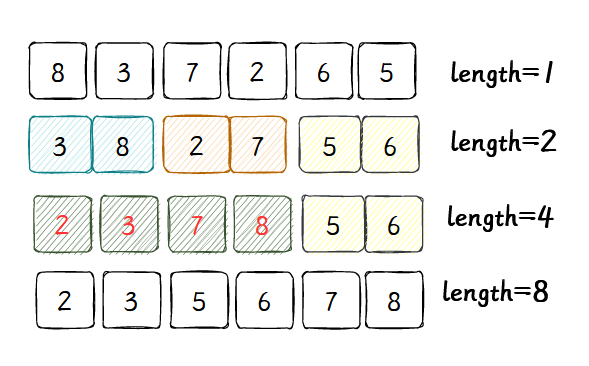
3 自底向上归并排序
不从整体开始切分,而是一开始把每一个元素当成一个列表,然后,自底向上地合并相邻的列表,重复利用开始的那张图。注意到,因为不同切分数组,可以直接迭代,无需递归。

- 首先获得N个子列表,每个子列表一个元素;
- 将相邻的两个子序列合并,得到 n / 2 n/2 n/2个长度为2的子序列;重复这个过程,直到整体有序。
伪代码描述:
function sort(A):
B = {} # 存放列表的列表,设下标从1开始
for each a in A do
B.append({a}) # 存入N个长度为1的子列表
N = B.length
while(N>1){
for i from 1 to floor(N/2) do
B[i] = merge(B[2i-1],B[2i]) # 每次取头两个合并
if Odd(N) then
B[ceil(N/2)] = B[N] # 处理落单的
N = ceil(N/2) # 向上取整
if B is empty then
return {}
return B[1]
严蔚敏的《数据结构(C语言版)》给出一种实现如下,写得真好:
/********************************************************
*函数名称:Merge
*参数说明:pDataArray 无序数组;
* int *pTempArray 临时存储合并后的序列
* bIndex 需要合并的序列1的起始位置
* mIndex 需要合并的序列1的结束位置
并且作为序列2的起始位置
* eIndex 需要合并的序列2的结束位置
*说明: 将数组中连续的两个子序列合并为一个有序序列
*********************************************************/
void Merge(int* pDataArray, int *pTempArray, int bIndex, int mIndex, int eIndex)
{
int mLength = eIndex - bIndex; //合并后的序列长度
int i = 0; //记录合并后序列插入数据的偏移
int j = bIndex; //记录子序列1插入数据的偏移
int k = mIndex; //记录子序列2掺入数据的偏移
while (j < mIndex && k < eIndex)
{
if (pDataArray[j] <= pDataArray[k])
{
pTempArray[i++] = pDataArray[j];
j++;
}
else
{
pTempArray[i++] = pDataArray[k];
k++;
}
}
if (j == mIndex) //说明序列1已经插入完毕
while (k < eIndex)
pTempArray[i++] = pDataArray[k++];
else //说明序列2已经插入完毕
while (j < mIndex)
pTempArray[i++] = pDataArray[j++];
for (i = 0; i < mLength; i++) //将合并后序列重新放入pDataArray
pDataArray[bIndex + i] = pTempArray[i];
}
/********************************************************
*函数名称:BottomUpMergeSort
*参数说明:pDataArray 无序数组;
* iDataNum为无序数据个数
*说明: 自底向上的归并排序
*********************************************************/
void BottomUpMergeSort(int* pDataArray, int iDataNum)
{
int *pTempArray = (int *)malloc(sizeof(int) * iDataNum); //临时存放合并后的序列
int length = 1; //初始有序子序列长度为1
while (length < iDataNum)
{
int i = 0;
for (; i + 2*length < iDataNum; i += 2*length)
Merge(pDataArray, pTempArray, i, i + length, i + 2*length);
if (i + length < iDataNum)
Merge(pDataArray, pTempArray, i, i + length, iDataNum);
length *= 2; //有序子序列长度*2
}
free(pTempArray);
}
几点说明:
- length代表的是单个子序列的长度;
- pTempArray 是上述文章提到的统一的工作区
- 实际排序时,并没有分为多个数组,而是只针对下标作逻辑上的合并,数据还在原来的数组中。
- 每次需要合并的两部分是
A[i,i+length) 和 A[i+length,i+2*length)注意右边界取不到。 - 下一次只需要把长度值翻倍即可,省去了许多开辟、释放空间的时间。
- 每次需要合并的两部分是
4 两路自然归并排序
从一个例子说起,如下图。虽然整个序列是混乱的,但是总有些部分是自然有序的(最差是一个数);想象一个两头都被点燃的蜡烛,同样的,我们从序列的两头同时开始寻找一个非递减的序列,如图中左右两端的 [8,12,14]和[15,7],合并到最右端;下一次找到后,合并到最最左端,这样做是为了平衡。
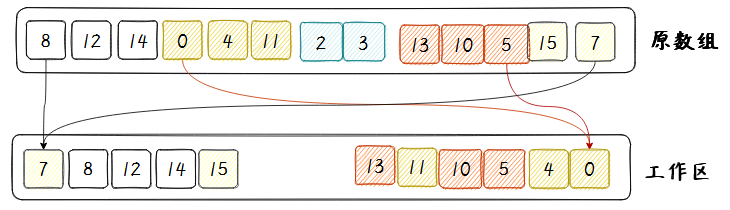
注意,上图数据归并后,左边是非递减,右边是非递增;且并不是一次完成所有的数据有序,而是多段有序,下面会进一步解释。
4-1 形式化描述
自然归并排序的不变性质,如下图所示:

- 任何时候,a之前和d之后的元素已经被扫描并归并到工作区的左右两端。
- 每次都需要将非递减子序列
[a,b)扩展到最长,同样的将[c,d)向左扩展到最长。 f(front)之前和r(rear)之后的元素是已经处理过的,可能包含若干有序的子序列,并非直接有序。- 奇数轮归并到
f这一边,偶数轮归并到r那一边。 - 关键中的关键,当扫描一轮后,原数组和工作区交换,继续归并,此时原数组(指针)指向工作区,且有序的子序列明显增多。
给出伪代码描述,如果还是看不明白建议抄一下伪代码:
function sort(A):
if A.length > 1 then
n = A.length
B = creat-array(n) # 创建工作区
loop
[a,b) = [1,1)
[c,d) = [n+1,n+1)
f = 1,r = n # 工作区的首尾指针
t = False # 控制从f还是r归并
while b < c do
repeat
b = b+1
until b >= c || A[b]<A[b-1]
repeat
c = c-1
until c<=b || A[c-1]<A[c]
if c < b then # 避免overlap 重叠
c = b
if b-a >=n then # 整个数组已经有序
return A
if t then # 从front归并
f = merge(A,[a,b),[c,d),B,f,1)
else #从rear归并
r = merge(A,[a,b),[c,d),B,r,-1)
a = b
d = c
t = not t # 换方向
exchange A<->B # 关键的一步,切换工作区
return A
# w 是工作区归并边界的下标 f 或 r
# det 表示方向 +1 或 -1
function merge(A,[a,b),[c,d),B,w,det):
while a<b and c<d do
if A[a]<A[d-1] then
B[w] = A[a]
a =a + 1
else
B[w] = A[d-1]
d = d-1
w = w+det
while a < b do
B[w] = A[a]
a=a+1
w=w+det
while c < d do
B[w]=A[d-1]
d=d-1
w=w+det
return w
4-2 代码实现
一些说明:
- 为了提高可读性,封装了C语言下的数组指针和区间类Range
- 参数很多时,建议先声明,然后统一赋值;注意到下标得到赋值在每一轮都需要更新
#include <iostream>
#include <cmath>
#include <ctime> //随机数组
using namespace std;
using Key = int;
// 定义一个左闭右开的区间
struct Range{
int l,r;
void set(int left,int right){
l=left;
r=right;
}
int size(){
return r-l;
}
};//[l,r);
// 封装C语言的数组
struct Array
{
Key* arr;
int len;
Array(int len):len(len){
arr=(Key*) malloc(sizeof(Key)*len);
}
Key& operator[](int i){
return *(arr+i);
}
Key& at(int i){
return *(arr+i);
}
void exchange(Array &B){
Key* tmp=arr;
arr=B.arr;
B.arr=tmp;
}
};
/// @brief 合并A的两个区间 Up Down到工作区B的w开始处
/// @param A 源序列
/// @param Up 位于左边的非递减序列
/// @param Down 位于右边的非递增序列
/// @param B 工作区,和源序列同样大
/// @param w 工作区的归并起点
/// @param det 控制w的增长方向,+1 or -1
/// @return 归并后的w值
int merge(Array &A, Range &Up, Range &Down,
Array &B, int w, int det)
{
for(;Up.l<Up.r && Down.l<Down.r;w+=det){
B[w]= (A[Up.l]<A[Down.r-1]) ? A[Up.l++]:A[--Down.r];
}
// 收尾工作
for(;Up.l<Up.r;w+=det){
B[w]=A[Up.l++];
}
for(;Down.l<Down.r;w+=det){
B[w]=A[--Down.r];
}
return w;
}
Array& merge_sort(Array &A){
if(A.len<2) return A;
Array B(A.len); //申请工作区
Range Up,Down; //左边的非递减区间,右边的非递增区间
int front,rear,dir;//工作区的前后指针和方向
for(;;){
Up.set(0,0);
Down.set(A.len,A.len);
front=0;
rear=A.len-1;
dir=1;
while(Up.r<Down.l){
do{
++Up.r; // 寻找非递减序列的右边界
}while(Up.r<Down.l && A[Up.r-1]<=A[Up.r]);
do{
--Down.l;
}while(Up.r<Down.l && A[Down.l]<=A[Down.l-1]);
if(Down.l<Up.r){
Down.l=Up.r; //消除可能的重叠
}
// 出口,已经有序
if(Up.size()>=A.len){
return A;
}
if(dir){
front=merge(A,Up,Down,B,front,1);
}else{
rear=merge(A,Up,Down,B,rear,-1);
}
Up.l=Up.r;
Down.r=Down.l;// 跳过已经扫描的部分
dir=!dir;
}
A.exchange(B);
}
return A;
}
void test(){
const int len=7;
Array A(len);
srand(time(NULL));
for(int i=0;i<len;i++){
A.at(i)=rand()%25+1;
cout<<A.at(i)<<" ";
}
cout<<endl;
merge_sort(A);
for(int i=0;i<len;i++){
cout<<A.at(i)<<" ";
}
cout<<endl;
}
int main()
{
test();
return 0;
}