电动力学专题：电磁波传播时的色散效应

news2024/11/29 0:31:32

本文中假定波动方程的性质足够好，不要杠，杠你就输了 @数学分析中的问题和XX
波动方程：\frac{\partial^2 u}{\partial t^2} - a^2 \frac{\partial^2 u}{\partial x^2} = 0......(1)

波的色散

波动方程描写的是以恒定速度a传播的非衰减波。方程（1）所描述的无界弦的总能量

我们可以证明，该波动方程对时间具有平移不变性，即能量守恒。

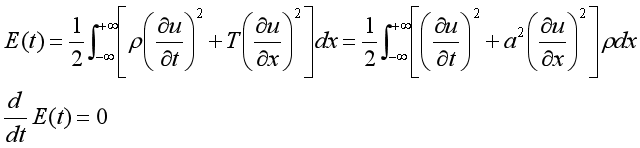
波动方程(1)可以分解为向左向右两个独立传播的波，不妨只考察向右传播的波，u(x,t)=f(x-at),即一阶波动方程 \frac{\partial u}{\partial t} + a\frac{\partial u}{\partial x}=0(2) 的解。

我们现在(2)中加上-\alpha \frac{\partial^2 u}{\partial x^2}(\alpha > 0)项，得方程（3）:

电动力学中要求我们找到方程谐波形式的解，即

u(x,t)=\int_{-\infty}^{+\infty} A(k)e^{i(kx-\omega t)}dk

代入(3)得，（3）的解为

u(x,t)=\int_{-\infty}^{+\infty} A(k)e^{i(kx-\omega t)} exp(-\alpha k^2 t)dk

且波数k和角频率\omega 满足\omega = ka - i\alpha k^2

我们可以看到，波的传播速度不变，但振幅衰减因子与波数有关，波形不断变化

我们现在(2)中加上\beta \frac{\partial^3 u}{\partial x^3}(\alpha > 0)项，可以观察到\omega = k(a-\beta k^2),也就是说，波长不同，波传播的速度也不同。

可以算出波的传播速度（相速） v_p = \frac{\omega}{k} = a - \beta k^2 与群速 v_g = \frac{d\omega}{dk}=a - 3\beta k^2

麦克斯韦方程组

波速 v = \omega / k = 1/\sqrt{\mu \eprsilon}

简单的说，不同频率的波在这里的传播速度是一样的

电磁波像速度v = \frac{\omega}{\beta}.简单的说，频率越大电磁波相速度越大且电磁波相速度小于无介耗媒质中的相速度。同样的，我们可以得到 v_g=\frac{d\omega}{d\beta} 但是难以求解。

趋肤效应是指交流电通过导体时，电流密度随电流方向的变化而发生变化的现象。在高频电磁场作用下，电流主要集中在导体表面附近，导体内部电流密度迅速衰减，这种现象称为趋肤效应。趋肤效应也叫肆虐效应，是交流电在导体中运动时，由于电磁感应作用导致电流集中在导体表面而产生的现象。越高频的交流电，在导体中运动时越容易产生趋肤效应。
波幅降职导体表面原值1/e时的传播距离为穿透深度，记作\delta = \sqrt{2/(\omega \mu \sigma)}

导体在高频下的电阻相当于厚度为\delta 的薄层的直流电阻
推导逻辑
- 导体内平均损耗功率密度 W = 1/2 Re(J* * E)
- 计算导体表面单位面积平均损耗功率 P = int W*dz
- P = I^2R = I^2/\sigma

因此，对应的电磁波的相位常数k_z可以表示为 k_z = \frac{2\pi}{\lambda}\sqrt{1-(\lambda \lambda_c)^2}。类似的，我们算出波导管内电磁的传播相速度 v_p = \omega/k_z
导行波的色散主要是由于边界条件对电磁波的制约作用
并非所有导行波都是色散波
- 例如由同轴线所引导的电磁波其主模是TEM波是一种非色散波，只有除主模以外的其它高次模才是色散波