1. 事务

场景：学工部整个部门解散了，该部门及部门下的员工都需要删除了。

在部门表当中维护的是部门的相关信息，在员工表当中维护了员工的相关信息，在员工表当中有一个字段dept_id关联的就是部门表的主键。

• 操作：

-- ================================事务==================================
-- 模拟一个解散部门的操作 --- 解散学工部
-- 删除学工部
delete from tb_dept where id = 1; -- 删除成功

-- 删除学工部下的员工
delete from tb_emp where dept_id = 1; -- 删除失败(操作过程中出现错误:造成删除没有成功)
                                      -- 在操作前后,数据出现了不一致的问题

• 问题：如果删除部门成功了，而删除该部门的员工时失败了，此时就造成了数据的                             不一致。

要解决上述的问题，就需要通过数据库中的事务来解决。 

导学：什么是事务，以及事务的控制操作和事务的四大特性

1.1 介绍 

事务是数据库当中非常重要的一个特性。

• 在实际的业务开发中，有些业务操作要多次访问数据库。
• 一个业务要发送多条SQL语句给数据库执行，需要将多次访问数据库的操作视为一个整体来执行，要么所有的SQL语句全部执行成功。
• 如果其中有一条SQL语句失败，就进行事务的回滚，所有的SQL语句全部执行失败。
• 简而言之：事务是一组操作的集合，它是一个不可分割的工作单位。事务会把所有的操作作为一个整体一起向系统提交或撤销操作请求，即这些操作要么同时成功，要么同时失败。
• 事务作用：保证在一个事务中多次操作数据库表中数据时，要么全都成功,要么全都失败。

提问：刚才在执行解散部门的这个业务操作时，涉及到两个操作，一个是删除部门，一个是删除               部门下的员工，由于它是属于同一个业务，也就意味着这两个操作是一个不可分割的工作               单位，属于一个事务，里面所涉及到的操作要么同时成功，要么同时失败，那为什么我们               刚才在测试的时候删除部门成功了，删除部门下的员工信息却失败了，而没有同时失败呢？

 回答：原因是在MySQL数据库当中，事务默认是自动提交的，也就是说，当我们在执行一条DML             语句的时候，一旦这条DML语句执行完成，MySQL当中的事务会立刻提交。这也就意味着             上面的这条SQL语句是一个事务，下面的这条SQL语句又是一个事务，也就是说，在我们               刚才执行解散部门这个业务操作的时候其实它是两个事务，第一条delete语句它是一个事               务，第二条delete语句它又是一个事务，所以就出现问题了。

如何解决？

• 需要将这两步操作控制在一个事务的范围内，此时就涉及到数据库当中的事务控制。            

1.2 操作 

我们可以在业务操作执行开始之前执行一个指令：start transaction；或者是begin；来开启一个事务。

当这一组操作当中，所有的操作都执行成功之后，我们再来提交事务。

• 提交事务就是把我们这次所执行的这些操作真正的提交到数据库来修改表结构当中的数据。

最后一步就是回滚事务，当我们这组操作当中有任何一个操作失败，此时就需要回滚事务。

• 回滚事务就是把所有的数据恢复到操作之前的样子。

MYSQL中有两种方式进行事务的操作：

1. 自动提交事务：即执行一条sql语句提交一次事务。（默认MySQL的事务是自动提交）
2. 手动提交事务：先开启，再提交。 

事务操作有关的SQL语句：

SQL语句	描述
start transaction; / begin ;	开启手动控制事务
commit;	提交事务
rollback;	回滚事务

手动提交事务使用步骤：

• 第1种情况：开启事务  =>  执行SQL语句   =>  成功  =>  提交事务
• 第2种情况：开启事务  =>  执行SQL语句   =>  失败  =>  回滚事务

-- =======================事务控制========================
-- 在该窗口开启了一个事务,只要这个事务还没有提交,在其它窗口当中是看不到我们所操作的数据的,因为其它窗口也相当于是一个事务,它们两者之间是相互隔离的。
-- commit是所有操作都成功执行之后才来执行的提交事务,只要有一个操作执行失败,我们要执行的是rollback回滚事务。
-- 一旦出现异常,我们就可以通过rollback回滚事务将删除掉的数据再恢复回来,从而保证在操作前后数据是一致的。
-- 这就是事务,要么同时成功,要么同时失败。
-- 开启事务
start transaction;

-- 删除学工部
delete from tb_dept where id = 1;

-- 删除学工部下的员工
delete from tb_emp where dept_id = 1;

-- 上述的这组SQL语句，如果如果执行成功，则提交事务
-- 提交事务(成功时执行)
commit;

-- 上述的这组SQL语句，如果如果执行失败，则回滚事务
-- 回滚事务(出错时执行)
rollback;

select * from tb_dept;
select * from tb_emp;

1.3 事务的四大特性(重点掌握)

原子性：原子指的就是不可再分的，事务是一个不可分割的最小操作单元，这个操作单元当中的                  操作要么全部成功，要么全部失败。

一致性：一致性指的是事务完成时必须使所有的数据都保持一致状态，不论是事务提交还是事务                  回滚都算事务完成了，只要事务完成了，所有的数据都保持一致状态。

隔离性： 隔离性指的是数据库当中所提供的隔离机制，保证事务在不受外部并发操作的影响下独                   立运行。

• 比如：在该窗口开启了一个事务,只要这个事务还没有提交,在其它窗口当中是看不到我们所操作的数据的,因为其它窗口也相当于是一个事务,它们两者之间是相互隔离的，这就是隔离性的体现。

• 隔离性我们是可以通过隔离级别去设置的，隔离性越高，事务越安全，但是效率也就越低，换隔离性我们一般不会手动去控制。

持久性：事务一旦提交或回滚，它对数据库当中数据的改变就是永久的。

• 举例：如果说你把一个事务提交了或者是回滚了，接下来你把数据库关了，下一次你再打                   开，数据依然是提交以及回滚之后的数据，对数据的改变是永久的。

事务的四大特性简称为：ACID

• 原子性（Atomicity） ：原子性是指事务包装的一组sql是一个不可分割的工作单元，事务中的操作要么全部成功，要么全部失败。

• 一致性（Consistency）：一个事务完成之后数据都必须处于一致性状态。

如果事务成功的完成，那么数据库的所有变化将生效。

如果事务执行出现错误，那么数据库的所有变化将会被回滚(撤销)，返回到原始状态。

• 隔离性（Isolation）：多个用户并发的访问数据库时，一个用户的事务不能被其他用户的事务干扰，多个并发的事务之间要相互隔离。

一个事务的成功或者失败对于其他的事务是没有影响。

• 持久性（Durability）：一个事务一旦被提交或回滚，它对数据库的改变将是永久性的，哪怕数据库发生异常，重启之后数据亦然存在。

 事务总结：

 

到此已经学习了MySQL数据库的设计，数据库的操作部分，包括单表的设计，单表的增删改查，以及多表的设计，多表的增删改查操作。

接下来学习最后一个部分数据库的优化 --- 提升查询效率最有效的方式 ---- 索引。

2. 索引 

导学：什么是索引，索引的数据结构，索引的具体操作语法，以及索引的具体操作

2.1 介绍 

概念：

索引(index)：是帮助 数据库 高效获取数据的 数据结构。

索引它的作用就是来高效获取数据的，换句话说索引就是来提高查询效率的，而且它的本质是一种数据结构，简单来讲，就是使用索引可以提高查询的效率。

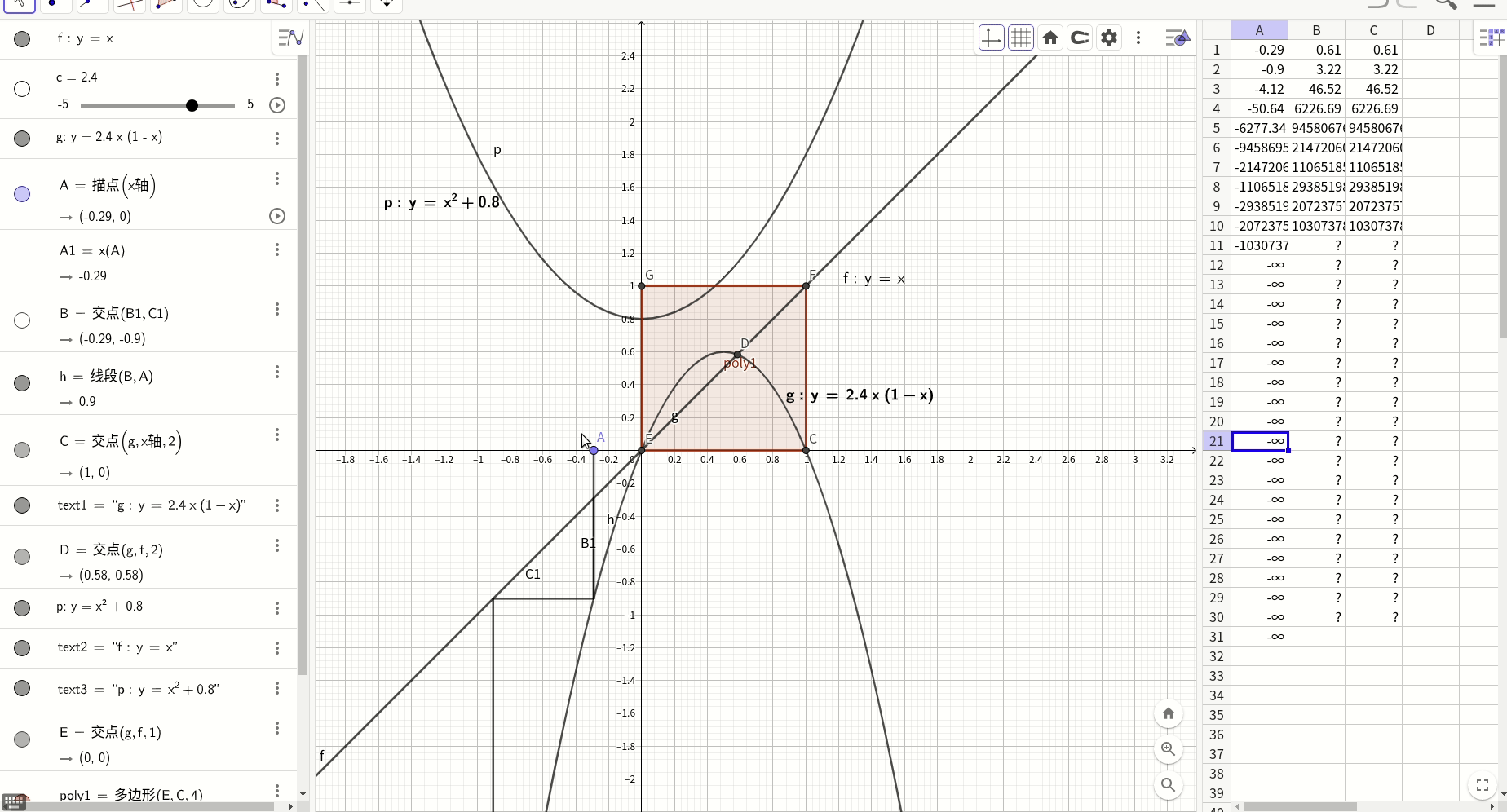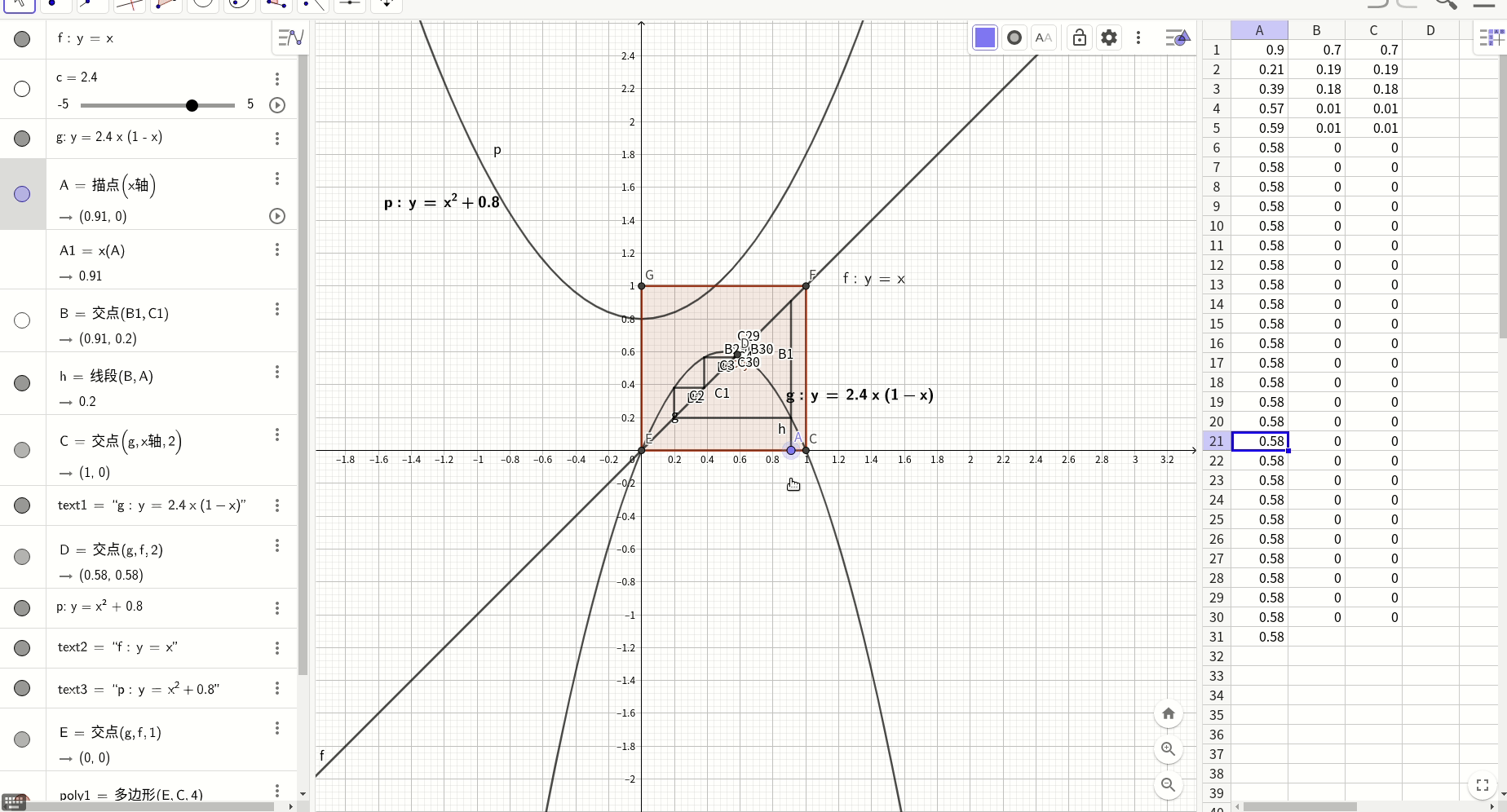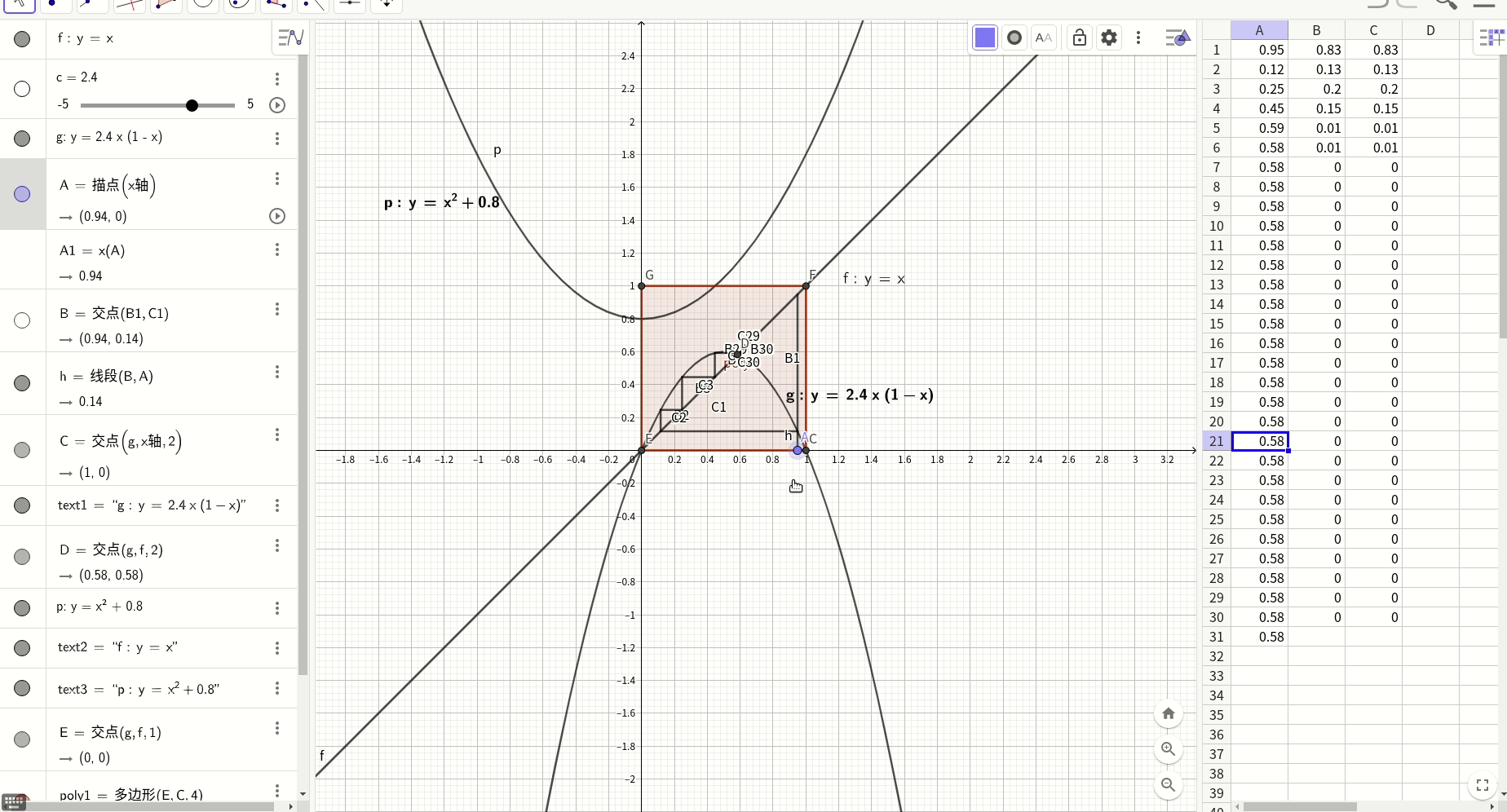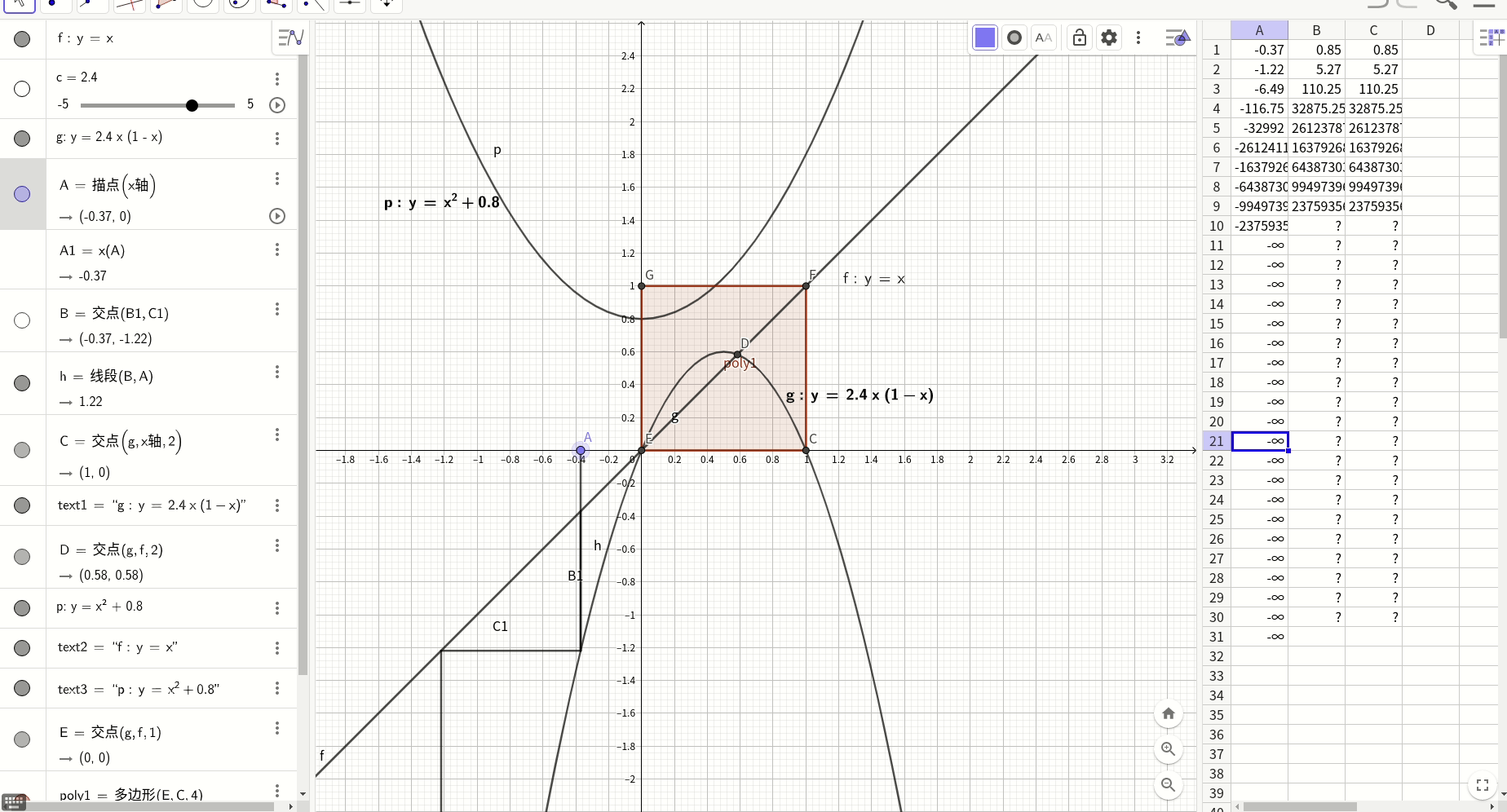
测试没有使用索引的查询：

添加索引后查询：

为该字段来构建索引，虽然这个过程是比较耗时的，但是这是一次性的操作。

-- 添加索引
create index idx_sku_sn on tb_sku (sn);  #在添加索引时，也需要消耗时间

-- 查询数据（使用了索引）
select * from tb_sku where sn = '100000003145008';

提问：在数据库当中没有索引的情况下它是如何查询的，有索引的情况下它又是如何查询的？

           通过索引是如何来提高查询效率的？

 

 

在没有索引的情况下，它就需要从第一条记录开始进行匹配查找，首先判断第一个值是不是我们要查找的，如果不是，再去找第二个，如果还不是，再去找第三个，继续往后找直到找到要查找的值。

提问：如果已经找到要查找的值了，还要不要继续往后找呢？

回答：如果要查找的该字段它不是唯一的，那我们还需要继续往后找，直到找到最后的一条记录，这就是没有索引的情况下，这种情况我们也称之为全表扫描。全表扫描的性能是非常低的，而且数据量越大，性能越低。

说明：上图所演示的二叉搜索树它仅仅是一个示意图，并不是真正的MySQL底层的索引结构。

如果我们为该字段建立了一个索引，它就会维护一个索引对应的数据结构，而这个数据结构，会大大的提高查询的效率。

提问：如果让你来实现这个索引，你会选择什么样的数据结构来实现索引呢？

注意：索引是用来提高查询效率的。

回答：用树形结构来实现索引，比如我们最为常见的二叉搜索树 / 二叉查找树

提问：以二叉搜索树为例，通过这样一个树形结构是如何来提高查询效率的？
在构建这个树形结构的时候，每一个结点都会去关联它的原始的数据记录，在二叉树当中，一个节点下面最多只能有两个子节点，二叉搜索树它的左子树上所有节点的值是要小于根节点的，而右子树上所有节点的值是要大于根节点的。

提问：有了二叉搜索树之后，现在我们要查询数据它又是如何查找的？
回答：如果构建了二叉查找树这样一个树形结构之后，接下来再进行查询的时候，就不用再去遍历整张表进行查询了，直接拿要查找的值与根节点的值进行比较，如果比根节点的值小，往左子树查找，如果大于根节点的值，往右子树查找。找到该节点后，又由于每一个节点又和原始的数据记录关联着，因此最终也就找到了原始的数据记录，这就是有索引的情况，在有索引的情况下进行数据记录的查询，就不用进行整表扫描了，我们只需要在索引结构上进行几次对比，就可以找到对应的数据，而且这个过程是非常高效的，查询效率会得到很大幅度的提升。

其实这个索引就类似于是一本书当中的目录，如果这本书当中没有目录，我们要查找某一章节的内容，就需要从第一页一直往后翻，直到找到这一章节的内容，类似于是一个全书扫描。

如果说我给这本书籍建立一个目录，那接下来我要查找某一章节的内容，我只需要去看一眼这个目录，我就知道这一章节的内容在第几页，那我就可以精准的定位到这一页的内容。 

索引的优缺点：

优点：

1. 提高数据查询的效率，降低数据库的IO成本。

2. 通过索引列对数据进行排序，降低数据排序的成本，降低CPU消耗。

缺点：

1. 索引会占用存储空间。

2. 索引大大提高了查询效率，同时却也降低了insert、update、delete的效率。

优点：索引可以提升数据库查询的效率以及排序的效率。

缺点：索引会占用磁盘空间。索引是一种数据结构，这种数据结构最终是要存储在磁盘文件当中               的。data目录下存放的就是MySQL的数据文件。

           索引虽然可以大大的提高查询的效率，但是同时却降低了增删改的效率。

           因为在进行增删改操作时，数据发生变化了，此时就需要去重新维护这个索引的数据结                   构，所以，我们在进行增删改的时候，除了需要去操作数据本身以外，还需要来维护这个               索引结构，那就会降低增删改的效率。

注意：在优点面前，索引的两个缺点可以忽略不计，因为对于现在的企业服务器来说，磁盘空间都是拿T来计算的，而且索引本身占用的磁盘空间也并不会太大。对于第二点降低增删改的效率就更不用担心了，因为对于一个正常的业务系统来说，查询会占到90%以上，增删改的频次本来就已经很低了，所以我们在进行业务操作时，主要考虑的是查询性能的优化。

2.2 结构

MySQL当中索引的数据结构

MySQL数据库当中支持的索引结构比较多

Hash索引 --- 哈希索引   B+Tree索引 --- B+树索引   Full-Text --- 全文索引

我们平时所说的索引，如果没有特别指明，都指的是MySQL当中默认的B+Tree索引结构。

在二叉搜索树当中，左子树上所有节点的值都是小于根节点的值，右子树上所有节点的值都是大于根节点的值，而且根节点的左右两个子树又都是一个二叉搜索树，而如果是一个二叉搜索树，又很容易出现一个问题，那就是偏向一边的情况 --- 瘸子现象。

如果我们在保存数据的时候，是根据数据的从大到小或者是从小到大的顺序来保存的，那此时就会将二叉搜索树退化成这样一个单向链表，此时，它的搜索性能就会大打折扣。这个时候，我们就可以选择平衡二叉树或者红黑树来解决这个问题，因为红黑树也是一颗平衡的二叉树。

但是，在MySQL数据库当中，并没有采用二叉搜索树或者是平衡二叉树或者红黑树来作为索引的数据结构。

思考：如果采用二叉搜索树或者是红黑树来作为索引的结构，有什么问题呢？
回答：最大的问题就是大数据量的情况下，层级较深，检索速度比较慢。因为不管是二叉搜索树还是红黑树，它一个节点下面只能有两个子节点，此时，在大数据量的情况下就会造成树的高度比较高，树的高度一旦高了，检索速度就会降低。

接下来，我们就来看一下在B+Tree结构当中，它又是如何来规避这个问题的？

B+Tree也叫多路平衡搜索树，首先，它是一颗平衡的树，

B+Tree的索引结构图：
在B+Tree当中，每一个节点是可以存储多个Key的，不像二叉树，二叉树当中一个节点只能存储一个Key，而且在B+Tree每一个节点当中，存储了N个Key就会有N个指针，如图，P1、P2、P3其实就是三个指针，这三个指针分别用来指向下一个磁盘块，黄色的区域我们就叫一个磁盘块，这个在数据库当中也叫页，页是数据库进行磁盘管理的最小单位。一个页它的大小是16KB。

这是B+Tree的第一个特点：在一个节点当中可以存储多个Key，有N个Key就会有N个指针，也就意味着这个节点会有N个子节点，多个子节点也就是我们提到的多路。

第二个特点：在B+Tree当中，上面的这些节点我们都称之为非叶子节点，下面的这层我们称之为叶子节点。B+Tree当中的非叶子节点它仅仅起到索引数据、查找数据的作用，它并不保存具体的数据，所有的数据都是在叶子节点这个部分来保存的，而且所有的Key也都会出现在叶子节点。

比如，在根节点当中有6这个Key，6这个Key在叶子节点当中也会有，在根节点当中还有38这个Key，38这个Key在叶子节点当中也存在。在根节点当中还有一个Key是67，67在叶子节点当中也有。也就是说，所有的Key都会在叶子节点出现，而且，在叶子节点当中会保存这个Key对应的数据，下面绿色的部分就是对应的数据。这是B+Tree的第二个特点。