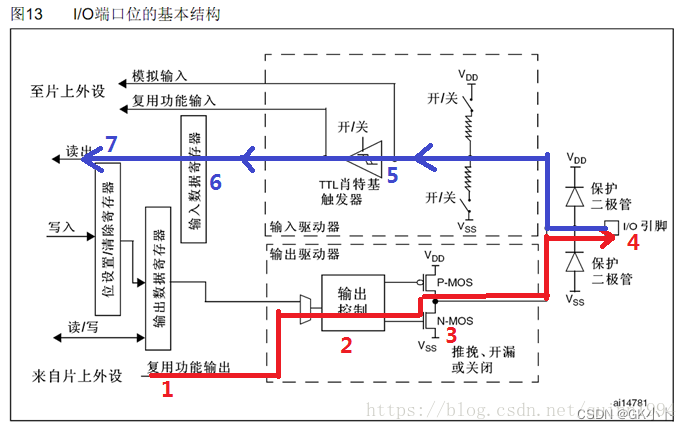
最近读高观点下的数学这本书，对书中介绍的布劳威尔不动点定理的有趣性质印象很深，原因是这个定理的某些性质能够解释我们生活中的一些常见现象，这里结合一个例题，聊以记录。

从一个数学题讲起：

f(x)是定义在[0,1]上的连续函数，并且0<=f(x)<=1.求证：至少存在一个ξ,使得f(ξ)=ξ;

证明过程比较简单，构造函数：

F(x)=f(x)-x

则,F(0)=f(0)-0 >=0, F(1)=f(1)-1<=0.

根据零点定理，函数F(x)在闭区间[0，1]上连续，且F(0)与 F(1)异号（即F(a)× F(b)<0），那么在开区间（a，b）内至少有函数F(x)的一个零点，即至少有一点ξ（0<ξ<1）使F(ξ)=0. 得证。

上面的例子拓展一下，给定函数f(x),那么就把满足f(x)=x这样的x称为不动点，其实就是题目中的ξ，有的函数有不动点，有的函数就没有不动点，比如下面的函数有不动点：

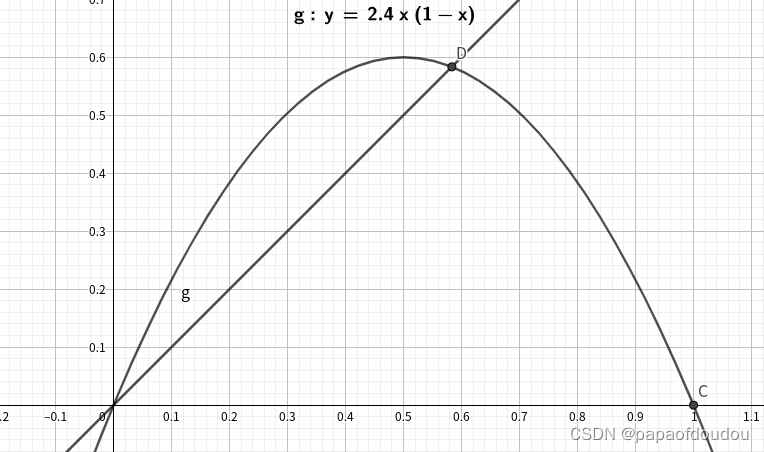
但是如下的函数y=x^2+0.8却没有不动点：

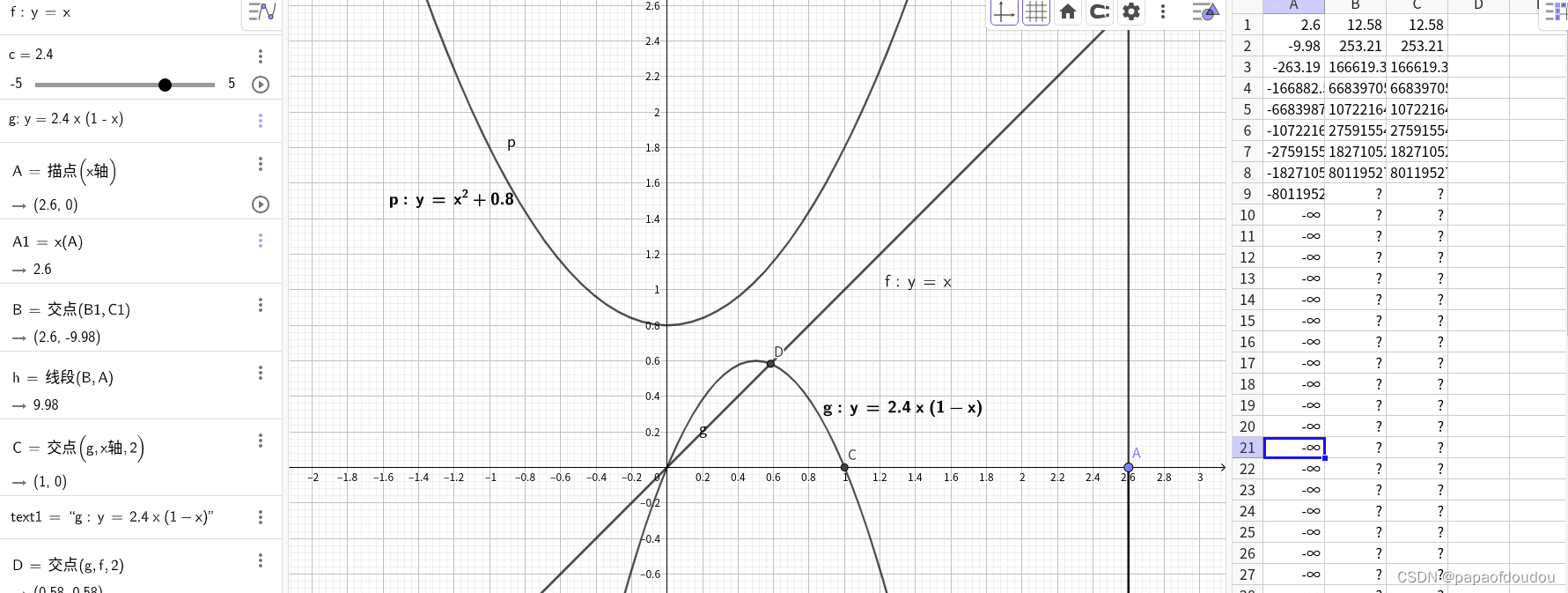
 那么什么样的函数会有不动点呢？我们从几何图形的角度反思一下刚才的题目，所谓满足f(x)=x的点，其实就是y=f(x)的图像与y=x这条直线的交点，在这个题目中，f(x)的定义域在[0,1]时，值域也是[0,1].所以，你的f(x)不管怎么画，只要它是连续的，必然会和正方形的对角线有1个交点，这个交点就是不动点：

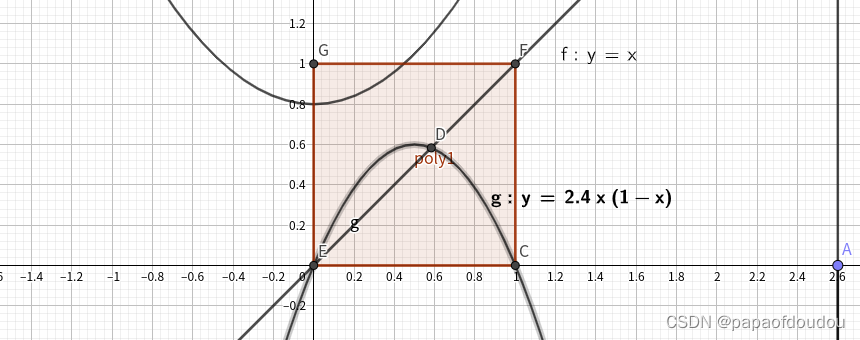
把上面的信息提取出来，就得到了布劳威尔定理的一维情景：f(x)是定义在闭区间I上的连续函数，如果它的值域也包含在I中，则它至少存在一个不动点，这个定理对于多维空间也是适用的。

可以用牛顿数值计算法找到这个不动点：

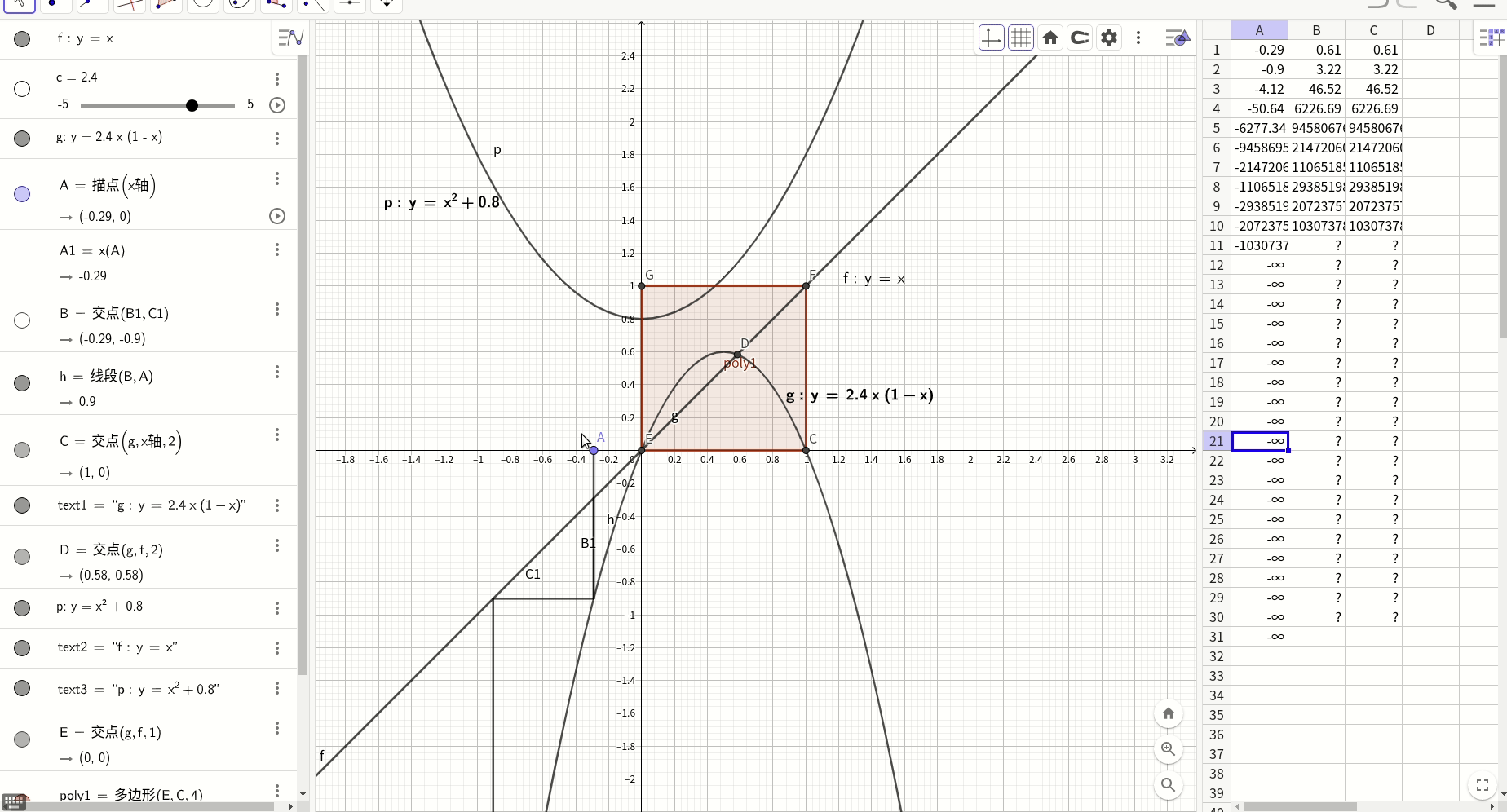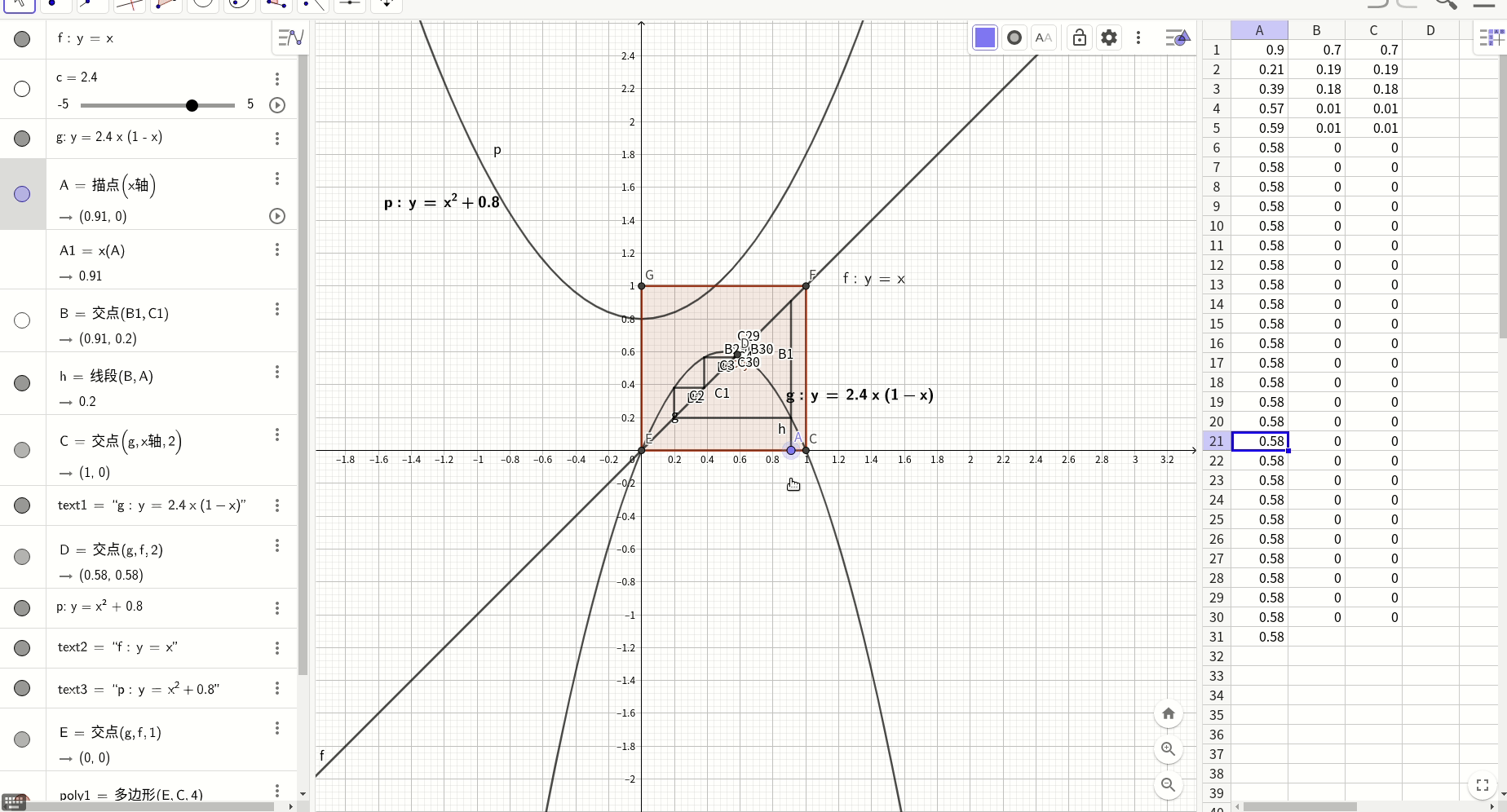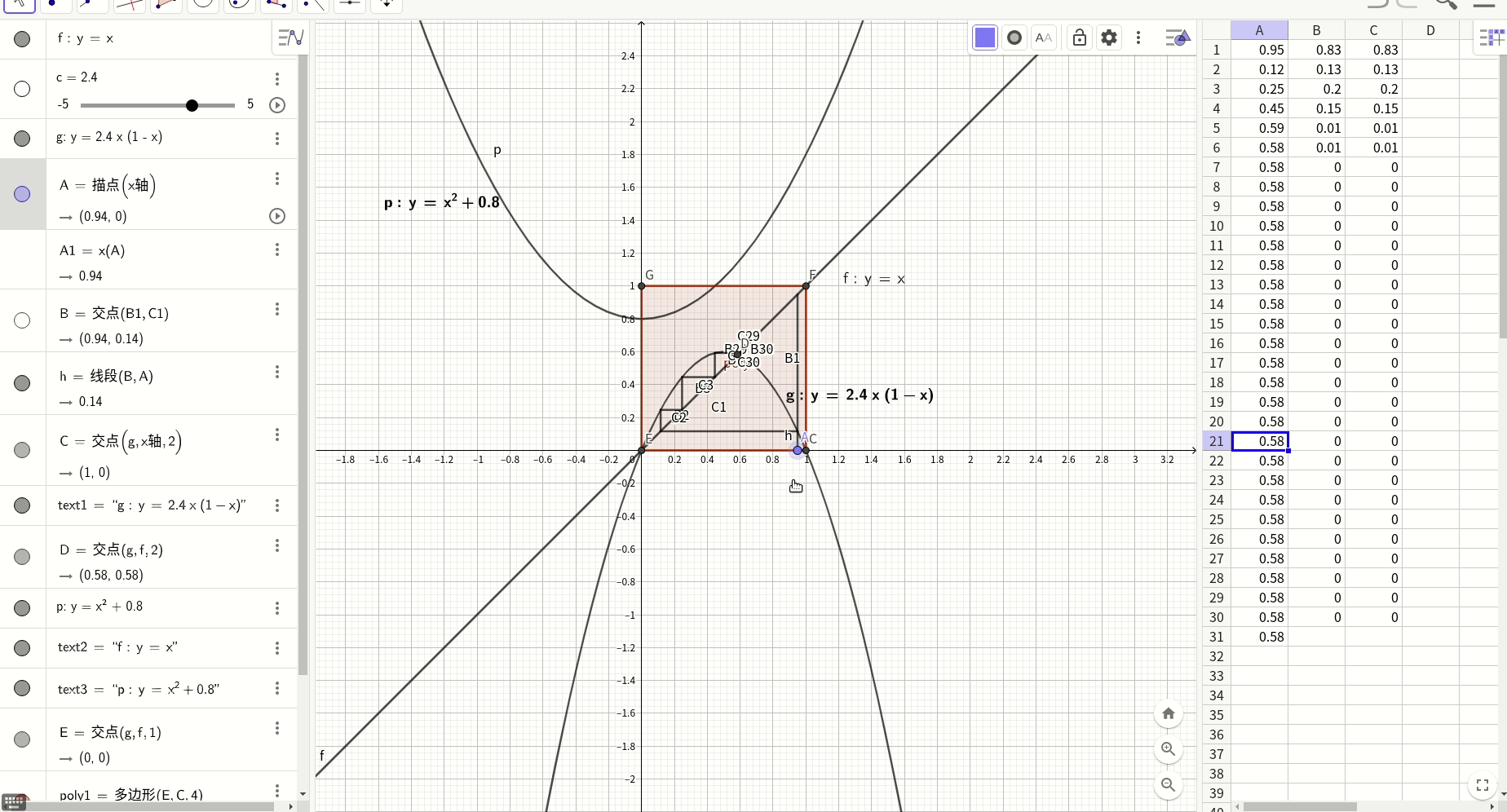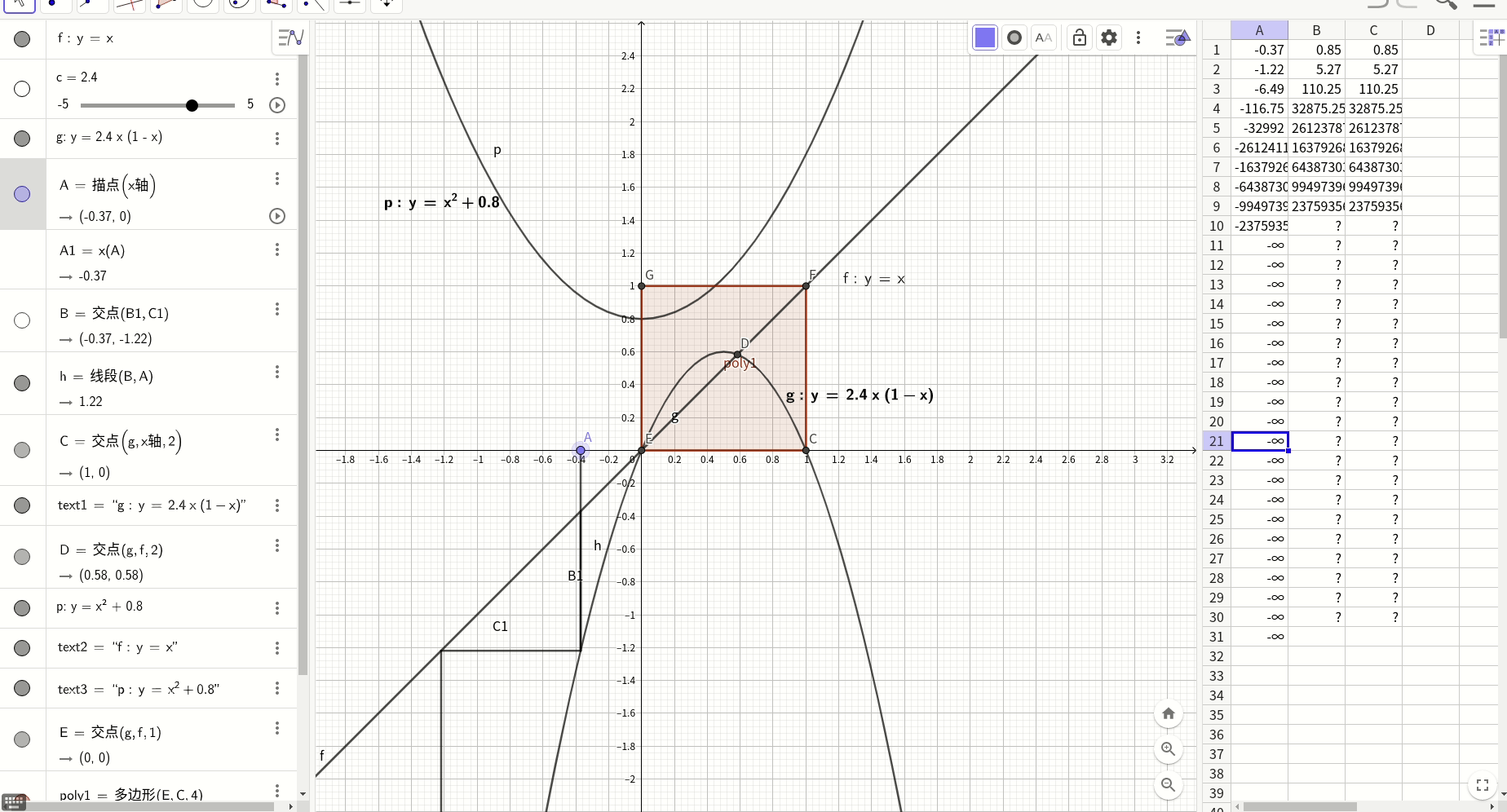
上图寻找不动点的轨迹在不动点两侧呈现出左吸右拉的特点，具体的说，在(-∞,0)时，寻找轨迹发散，无法找到不动点，但是在[0,不动点]区间，轨迹收敛于不动点，同样，[不动点，1]区间收敛，但是(1,∞)又开始发散，所以看起来围绕不动点的[0,1]区间有点类似于黑洞视界，主要进入它的势力范围，马上被吸入不动点，否则则是发散到无穷远处。

---

结束