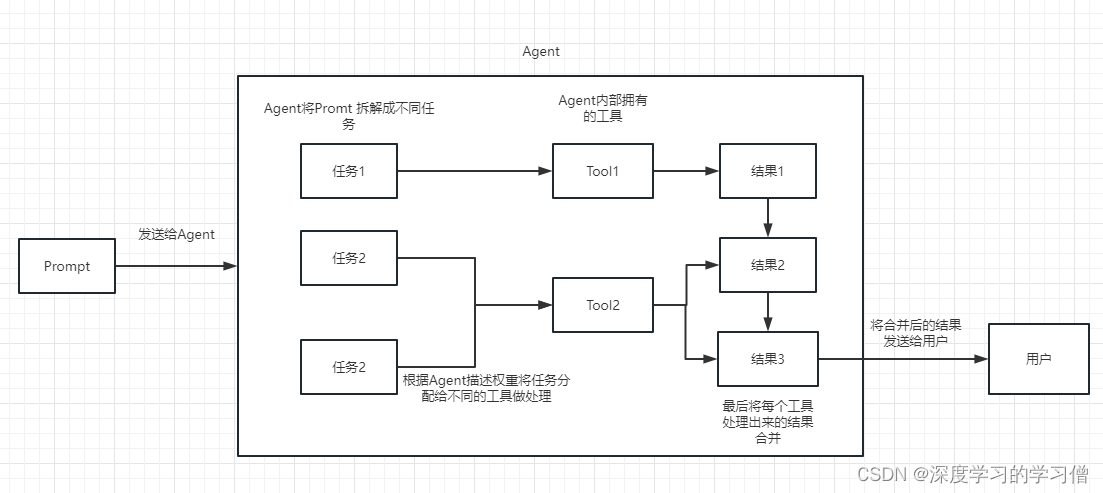
线段树暴力修改

 

关键是每个数取余操作，看似我们如果暴力改的话m*n肯定超时了

容易发现一个数小于给定模数的时候，取模不会发生改变，而大于给定模数的时候我们得到的最大的结果是x/2向上取整，结果一定小于等于这个数字,这里我想说的是任意一个数字它最多取模不超过log次就会变成0或者1，因此复杂度就是m*logn*log（ai）

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
typedef long long ll;
struct Segment{
	int l,r;
	ll maxn;
	ll sum;
}tr[N<<2];
ll w[N];
int n,m,l,r,x,k,op;


void pushup(int u){
	tr[u].maxn = max(tr[u<<1].maxn,tr[u<<1|1].maxn);
	tr[u].sum = tr[u<<1].sum + tr[u<<1|1].sum;
	
}

void build(int u,int l,int r){
	if(l==r)tr[u] = {l,r,w[l],w[l]};
	else{
		tr[u] = {l,r};
		int mid =l+r>>1;
		build(u<<1,l,mid),build(u<<1|1,mid+1,r);
		pushup(u);
	}
}
void modify1(int u,int l,int r,int x){
	if(tr[u].l>=l&&tr[u].r<=r){
		if(tr[u].maxn<x)return;
	    if(tr[u].l == tr[u].r){
	    	tr[u].maxn = tr[u].maxn%x;
	    	tr[u].sum  =tr[u].sum%x;
	    	return;
	    }
	}
	
	int mid = tr[u].l+tr[u].r>>1;
	if(l<=mid)modify1(u<<1,l,r,x);
	if(r>mid)modify1(u<<1|1,l,r,x);
	pushup(u);
}

void modify2(int u,int k,int v){
	if(tr[u].l==tr[u].r&&tr[u].l==k){
		tr[u].maxn = v;
		tr[u].sum  =v;
		return;
	}
	
	int mid = tr[u].l+tr[u].r>>1;
	if(k<=mid)modify2(u<<1,k,v);
	if(k>mid)modify2(u<<1|1,k,v);
	pushup(u);
}

ll query(int u,int l,int r){
	if(tr[u].l>=l&&tr[u].r<=r)return tr[u].sum;
	
	ll res=0;
	int mid = tr[u].l+tr[u].r>>1;
	if(l<=mid)res = query(u<<1,l,r);
	if(r>mid)res += query(u<<1|1,l,r);
	return res;
	
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>w[i];
	build(1,1,n);
	while(m--)
	{
		cin>>op;
		if(op==1){
			cin>>l>>r;
			cout<<query(1,l,r)<<endl;
		}else if(op==2){
			cin>>l>>r>>x;
			modify1(1,l,r,x);
		}else{
			cin>>k>>x;
			modify2(1,k,x);
		}
	}
}