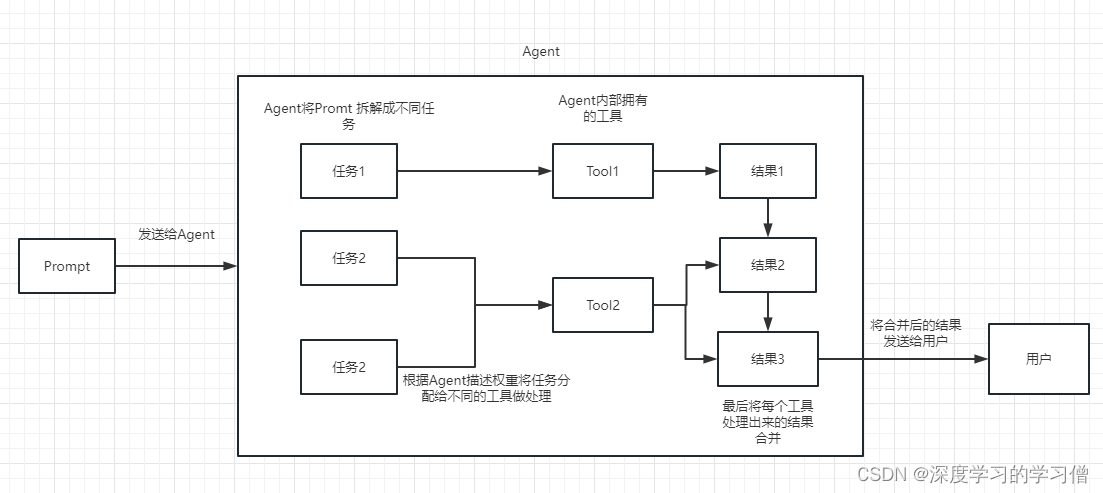
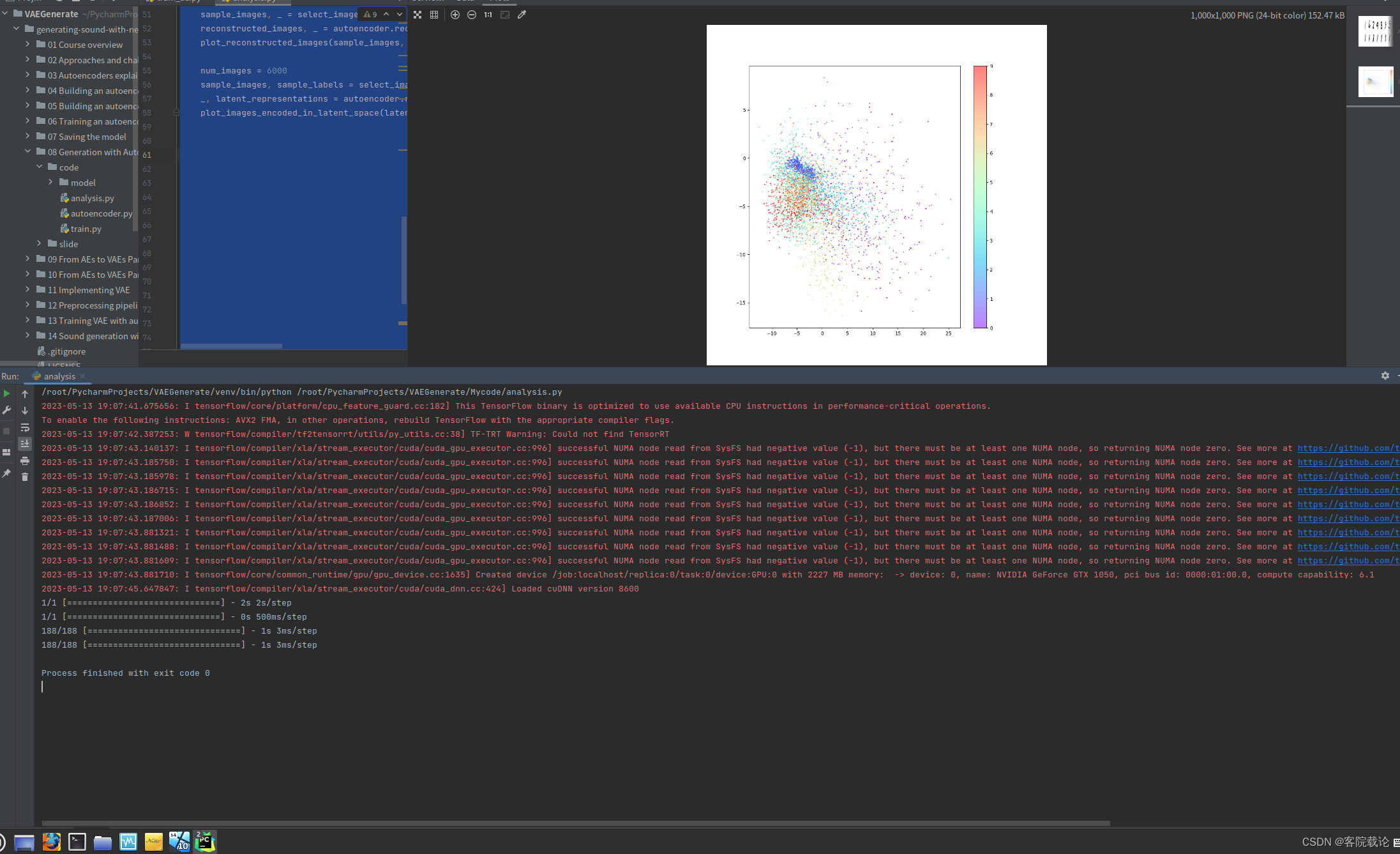
《编程思维与实践》1069.第一位数字
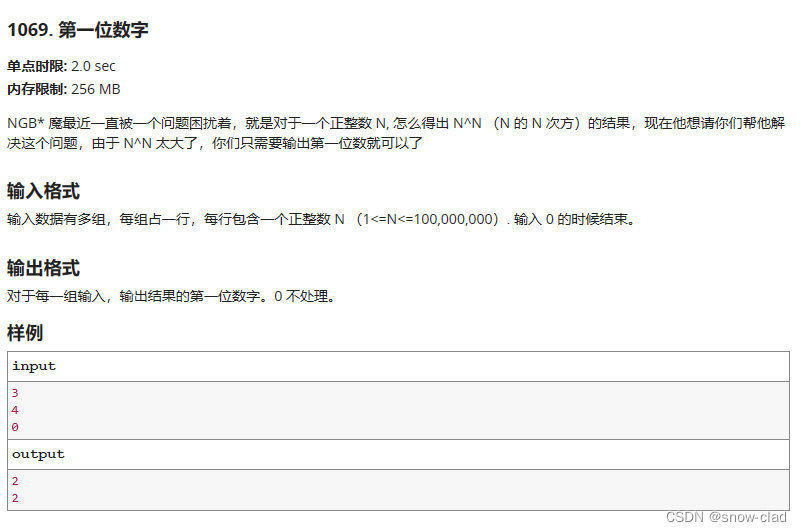
题目
思路
由于正整数N的N次方最大可以为 1 0 8 ⋅ 1 0 8 10^{8\cdot 10^8} 108⋅108,加上数据可能有很多组,所以直接采用大整数计算次方这方法很可能超时,
这里给出一种数学算法:
幂指函数通常的处理方式是取对数将乘方转化为乘法:
N N = 1 0 N l g N = 1 0 [ N l g N ] + { N l g N } = 1 0 [ N l g N ] ⋅ 1 0 { N l g N } N^N=10^{NlgN}=10^{[NlgN]+\{NlgN\}}=10^{[NlgN]}\cdot10^{\{NlgN\}} NN=10NlgN=10[NlgN]+{NlgN}=10[NlgN]⋅10{NlgN},
其中[x]表示取整,{x}表示取小数部分.
那么 1 0 [ N l g N ] 10^{[NlgN]} 10[NlgN]为10的倍数,后半部分 1 < 1 0 { N l g N } < 10 1<10^{\{NlgN\}}<10 1<10{NlgN}<10 且为小数,
只需再取出其整数部分即为幂指函数的第一个数字(类似科学计数法).
代码
#include<stdio.h>
#include<math.h>
int main()
{
int n;
while(scanf("%d",&n)!=EOF)
{
if(n!=0)
{
int first_number=0;
double temp=n*log10(n)-(int)(n*log10(n)); //取出小数部分
first_number=(int)(pow(10,temp));
printf("%d\n",first_number) ;
}
}
return 0;
}
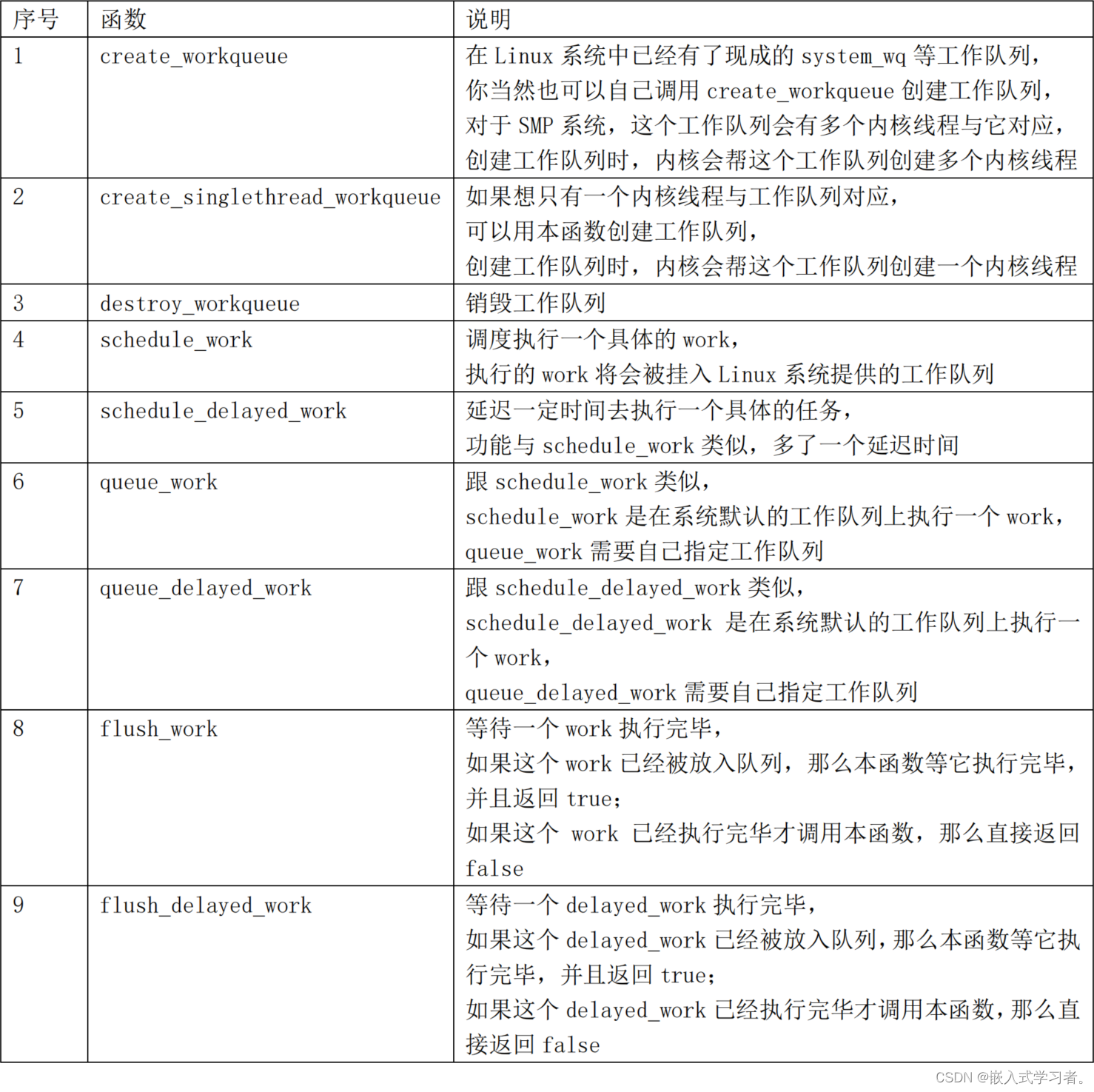







![[ 云计算 华为云 ] 华为云开天 aPaaS:构建高效的企业数字化平台(下)](https://img-blog.csdnimg.cn/img_convert/721ffe589e0c64aa061b6f318d09a0e7.png)