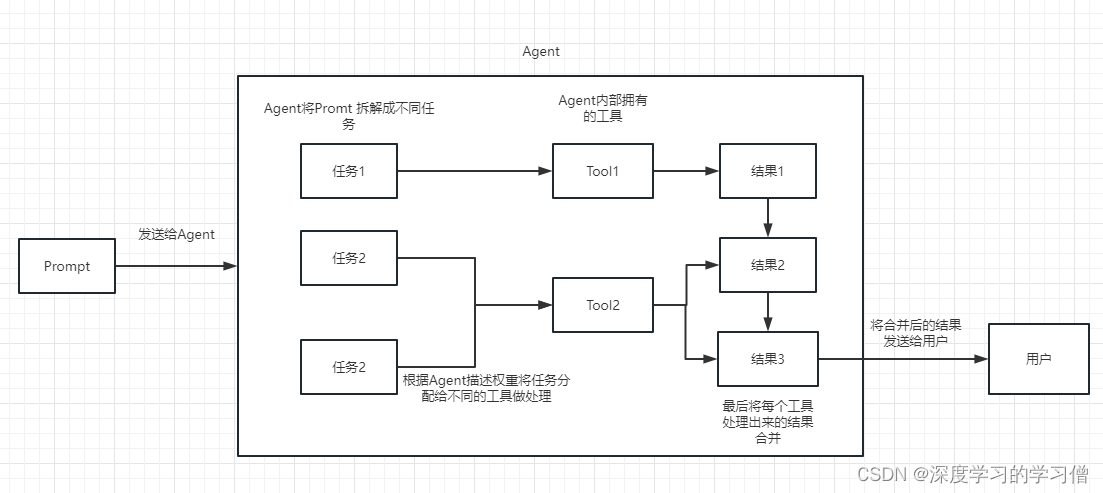
1 引入情境

我记得小时候玩过推箱子游戏，也是如下图这种，四周由深色的方格作为墙壁，白色的地方是可以通过的。现在想要从红色方格出发走到黄色方格，能有什么好办法呢？

注意到，对于计算机没有全局的观念，并不像人一眼就能看到出路。当然迷宫巨大无比时，人也是看一步走一步，很有可能沿着看似正确的判断却走入死胡同。因此，比较明智的方式是：

不断去尝试，再检查是否合理，不合理还得能退回。

尝试，从当前点考虑，它上下左右的下一步能不能走？
- 可以走，就要记录这个位置，怎么记录？
  - 用一个列表记录走过的点
  - 出现分叉会有多个列表，也得存一下
- 不能走，就尝试其他位置，都是什么点不能走？
  - 走过的点，不能再走，否则转圈。
  - 下一步是围墙，走不动。
如果是死胡同，还得退一步，怎么退回？
- 考虑栈结构，以前出现的、未处理的岔路口，放在栈里，当前死胡同就从栈顶弹出丢掉，再从栈顶取就回到了以前可走的地方。

2 形式化描述与分析

迷宫：用矩阵来描述，0代表可以通过，1代表墙壁，不能通过；转化为实际的节点图，如下所示。走过的点：用下标（X,Y）表示，自然路径就是一系列的坐标点。

            {0,0,0}-->{S,A,B}
            {1,0,1}-->{1,C,1}
            {1,0,0}-->{F,E,G}

下图展示了，记录路径的栈的变化；每次都是取出栈顶路径：

若当前末尾的下一个节点可达，加入到路径中，并重新入栈；
若当前末尾已经是死胡同，弹出后什么也不做。
若当前节的末尾已经是终点，则放入可达路径的队列里。

看上去在最坏的情况下，每个位置都有上下左右四个方向可选，好像是O( $4^N$ ），但实际上因为标记了走过的点，每个点最坏均被访问一次，时间复杂度是O(N)。因为用到了栈来存储候选路径，空间复杂度是O( $N^2$ )。

3 代码实现

注：在判断下一个节点是否已经被访问过，这里用的是在当前路径里检索；当然也可以用一个标记访问的矩阵，但需要额外的空间。

#include <iostream>
#include <vector>
#include <stack>

using namespace std;

// 迷宫问题
class Solution
{
    using Maze= vector<vector<int> >; //存放迷宫的二维数组
    using Pos = pair<int,int> ; // 坐标 (i,j)
    using Path = vector<Pos>; // 路径
    using Stack= stack<Path>; // 存放路径
public:
    vector<Path> solve_maze(const Maze &m,const Pos s,const Pos e){
        Stack S;
        S.push(vector<Pos>{s});
        vector<Path> L; //所有可能到达终点的路径

        while(!S.empty()){
            Path P=S.top();S.pop();
            Pos pn=P.back();
            if(e==pn){ //末尾就是终点
                L.push_back(P);
            }else{
                for(const auto pos : adj(m,pn)){
                    if(not_in(pos,P)){ //找到一个可行的节点
                        P.push_back(pos);
                        S.push(P);
                    }else{
                    ; //没有下一步可走，直接放弃这条路
                    }
                }
            }
        }
        return L;
    }
		//这一步也可以用一个全局的visited数组来标记
    bool not_in(Pos p,Path P){
        // 检查p是否不在路径P中
        for(const auto &pos:P){
            if(pos==p){
                return false;
            }
        }
        return true;
    }

    vector<Pos> adj(const Maze &m,Pos now){
        // 找出now的下一个可访问的邻居节点放入队列
        vector<Pos> pos_vec;
        int x=now.first;
        int y=now.second;

        int ds[4][2]={{0,1},{1,0},{-1,0},{0,-1}};
        for (size_t i = 0; i < 4; i++)
        {
            int nx=ds[i][0]+x;
            int ny=ds[i][1]+y;

            if (0 <= nx && nx < m.size() &&
                0 <= ny && ny < m[0].size() &&
                m[nx][ny] == 0)
            {
                pos_vec.push_back(Pos(nx, ny));
            }
        }
        return pos_vec;
    }

    void test(){
        Maze m={
            {0,0,1,0,0,0},
            {1,0,1,0,1,1},
            {0,0,0,0,0,0},
            {1,1,1,0,1,0},
            {0,0,0,0,1,1},
            {0,1,1,0,0,0},
        };

        Pos s(0,0),e(5,5);
        vector<Path> paths=solve_maze(m,s,e);
        for(auto &path:paths){
            for(auto &pos:path){
                cout<<"{"<<pos.first<<","<<pos.second<<"} ";
            }
            cout<<endl;
        }
    }
     
};


int main()
{
    Solution sol;
    sol.test();
    return 0;
}