线索二叉树操作详解（详细图例+cpp实现+源码）

news2024/10/7 3:42:31

文章目录

  • 线索二叉树
    • 中序线索二叉树
  • 构造线索二叉树
    • 节点的线索化
  • 其他操作
    • 销毁二叉搜索树
    • 获取中序遍历的第一个节点
    • 获取中序遍历的最后一个节点
    • 输出中序遍历序列
    • 逆序输出中序遍历序列
    • 源码

线索二叉树

线索二叉树又称为二叉树的线索化。

在一个具有n个节点的二叉树中，它含有n+1个空指针链域，如果我们把这些空指针链域利用起来，用它来记录当前节点的前驱节点与后继节点，这些指针被称为线索。 加上线索的二叉树成为线索二叉树。

线索二叉树：

  • 先序线索二叉树
  • 中序线索二叉树
  • 后序线索二叉树

我们在本节主要讨论中序线索二叉树。

线索二叉树的优势：

  1. 利用线索二叉树进行中序遍历时，不必采用堆栈处理，速度较一般二叉树的遍历速度快，且节约存储空间。
  2. 任意一个结点都能直接找到它的前驱和后继结点。

中序线索二叉树

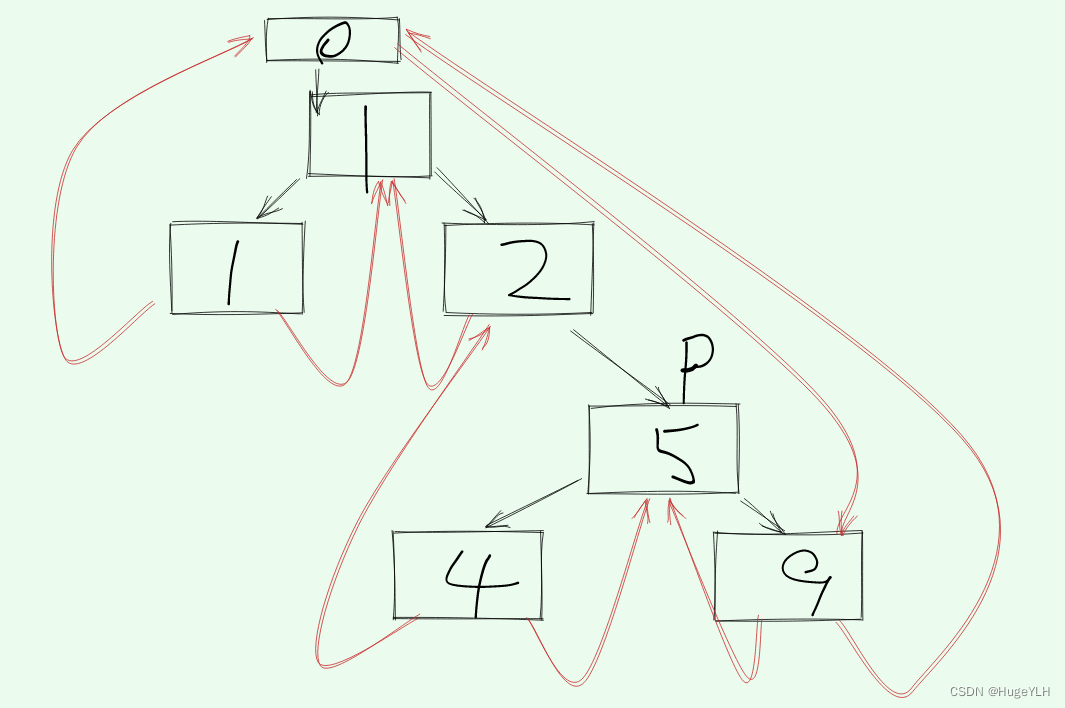
解析： 中序线索二叉树

这颗二叉树的中序遍历结果： 1 1 2 4 5 9 注意：我们使用了一个头节点（值为0）作为特殊的线索，在二叉树中本身并不包含这个头节点。

黑色指针链： 代表节点之间的正常的左右孩子关系。
红色指针链： 代表线索，即指针此节点的前驱与后继节点

注意：我们所讨论的前驱与后继都是根据这个二叉树的中序遍历的序列的位置关系。

  1. 根节点的左子树 1： 它是一个叶子节点，所以具有线索，左线索指向前驱节点，但是注意由于其前驱为空，所以规定他指向头节点；右线索指向其后继，在中序遍历中指向根节点1。
  2. 节点2：它的左为子树为空，所以它应该具有左线索，指向其前驱，应该为根节点1.
  3. 节点4：同第一步的节点1一致，具有左线索与右线索，分别指向前驱与后继节点，即节点2和节点5.
  4. 节点9：它是中序遍历的末尾节点，也是叶子节点，左线索指向前驱，即它的中序遍历前一个节点5；右线索指向后继，它没有后继，因此指向头节点。
  5. 注意：头节点也应该具有线索，左线索指向根节点，右线索指向这颗树的中序遍历的最后一个节点，即最右节点。

在这里插入图片描述

构造线索二叉树

我们经过上面的图分析后，可以得知：线索二叉树其实就是普通的二叉树，然后又加了指向其前驱与后继的线索。
那么如何表示左右指针链与线索呢？

存储结构：

template <typename T>
struct TreeNode
{
	T data;		//节点的值
	TreeNode* pleft, * pright;	//左右指针
	int ltag, rtag;		//表示有没有左右线索
};

  • ltag：是否具有左线索

    • 值为0： 直接用作普通的指针链即可，pelft指向其左孩子节点
    • 值为1： 它具有线索：此时pleft指向其当前节点的前驱节点。

  • rtag：是否具有右线索

    • 值为0： 直接用作普通的指针链即可，pright指向其右孩子节点
    • 值为1： 它具有线索：此时pright指向其当前节点的后继节点。

节点的线索化

当我们明确了二叉树节点的存储结构之后，我们便可以按照我们的思路来完成线索化了。

主要思路：
中序遍历一颗树，在中序遍历的过程中，检查当前节点的左右指针是否为空，为空则指向当前节点的前驱节点与后继节点。

请注意：既然需要前驱节点与后继节点，那么我们显然需要一个 pre节点，即指向当前节点的前驱节点的指针，用它来连接。

过程：

  1. 首先创建一个头节点pHead，用它来确保中序遍历的序列的首元节点和尾节点能够被线索化。
  2. 首先遍历左子树。
  3. 如果当前遍历的节点 p->pleft 不为空，则 p->ltag 置为0； p->pright 不为空，则 p->rtag 置为0，表示左右指针不需要线索化。
  4. 如果当前遍历的节点 p->pleft 为空，则 p->ltag 置为1，p->pleft指向其前驱节点 pre ； p->pright 为空，则 pre ->rtag 置为1，pre->pright指向其后继节点 p，表示左右指针需要线索化。（注意这个右线索化时，我们当前节点是p，前驱节点是pre，我们既然要让 p 连接后继节点，不如反过来让pre连接p。）
  5. 然后遍历右子树，递归，执行相同的操作。

代码示例：

template<typename T>
TreeNode<T>* Tree<T>::_createThread_Tree(TreeNode<T>* bt)
{
	//增加一个头节点
	TreeNode<T>* pHead = new TreeNode<T>{ 0,nullptr,bt,0,1 };
	//1. 判断这颗树是否是空的。
	if (bt == nullptr)
	{
		pHead->ltag = 0;
		pHead->pleft = pHead;
		pHead->rtag = 1;
		pHead->pright = nullptr;
	}
	else
	{
		//2. bt不为空树，则开始线索化。
		pHead->pleft = bt;	//（1）首先头节点的左指针线索化树根节点
		pre = pHead;		//（2）前驱节点首先设置为头节点
		_Thread(bt);		//（3）开始树中各个节点的线索连接
		//结束后，pre指向根节点  进行头节点根节点的连接
		pHead->pright = pre;	
		pre->rtag = 1;				
		pre->pright = pHead;
	}
	//返回头节点
	return pHead;
}
template<typename T>
void Tree<T>::_Thread(TreeNode<T>*& bt)
{	
	if (bt != nullptr)
	{
		//递归进入右子树，开始线索化
		_Thread(bt->pleft);	
		//直到其左指针为空，则需要将左指针线索化。
		//左指针指向其前驱节点，ltag标记为1
		if (bt->pleft == nullptr)
		{
			bt->pleft = pre;
			bt->ltag = 1;
		}
		else
		{
			//左指针不为空，则不需要线索化，ltag设置为0
			bt->ltag = 0;
		}
		//如果节点右指针为空，则需要将右指针线索化。
		//右指针指向其后继节点，rtag标记为1
		//注意： 当前节点与后继节点的连接可以转换为 ---> 前驱节点与当前节点(当作后继节点)的连接
		if (pre->pright == nullptr)
		{
			pre->pright = bt;
			pre->rtag = 1;
		}
		else
		{
			pre->rtag = 0;
		}
		//每次完成一个节点的操作后，前驱节点记得要更新为当前节点，然后当前节点接着往下遍历
		pre = bt;
		_Thread(bt->pright);	//递归进入右子树，开始线索化
	}
}

如果你对 _Thread线索化函数感到难以理解，我们来一步步图解这个过程：

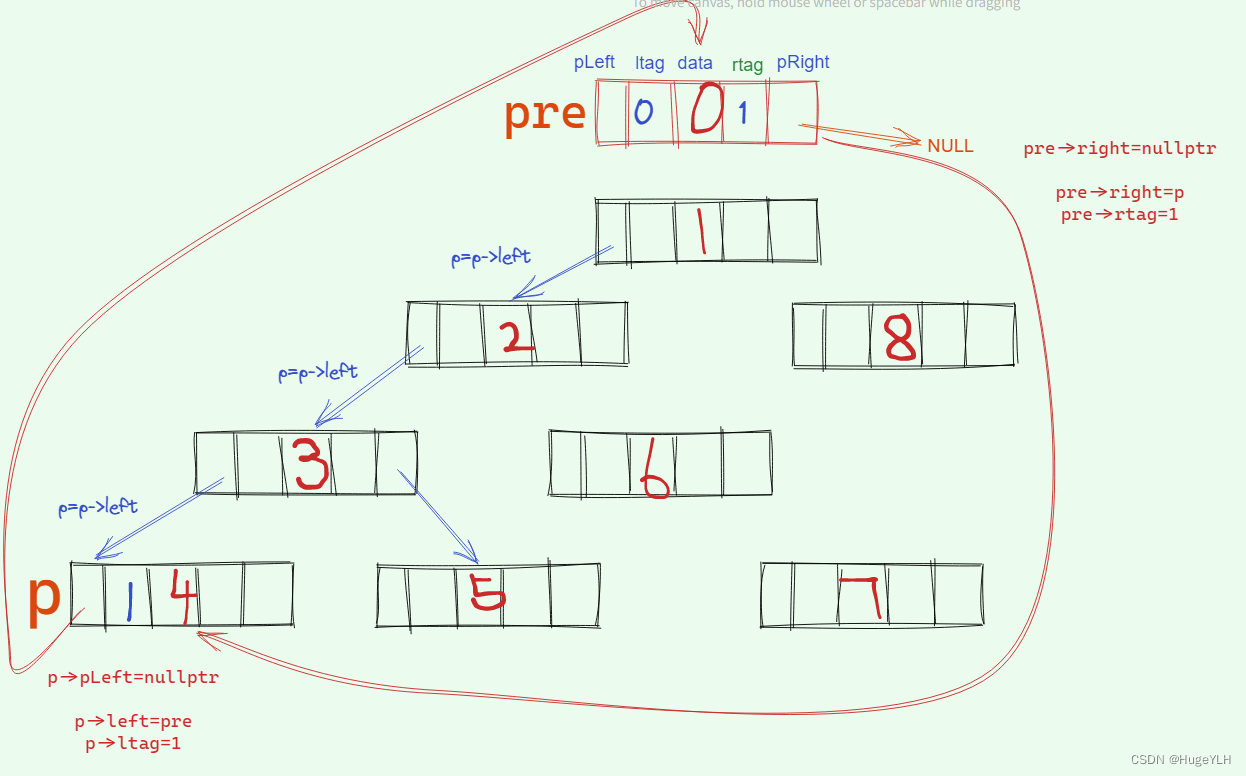
  1. 首先p一路递归到其左指针等于空的时候，开始线索化：左指针指向其前驱节点，此时pre默认为头节点（我们自定义的），左指针指向头节点，ltag标记为1；pre的右指针为空，pre的右指针指向当前节点，rtag标记为1，接着递归进入节点4的右子树。
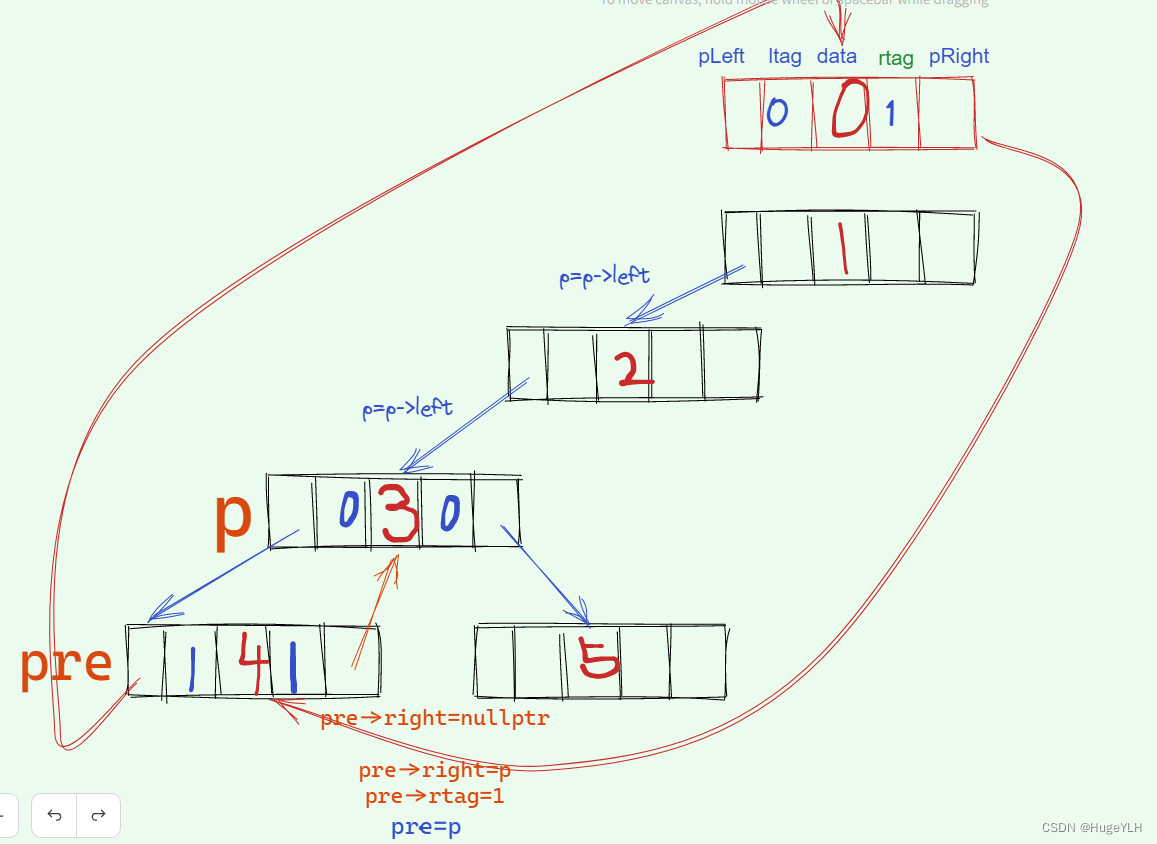
    在这里插入图片描述

  2. 节点4右指针为空，因此递归返回一层，返回到节点3。pre指向其前驱节点4。可以发现节点3的左指针不为空，因此ltag标记为0，无需对左指针进行线索化。pre的右指针为空，进行pre右指针的线索化，连接其后继节点。pre的pright连接当前节点p，标记ltag为1，此时就完成了节点4的线索化。
    在这里插入图片描述

  3. 接着递归进入节点3的右子树中，到达节点5，它的左指针为空，因此进行左线索化，连接其前驱节点pre，标记节点5的ltag为1。此时 节点3的线索化就完成了！ 然后递归进入节点5的右子树。
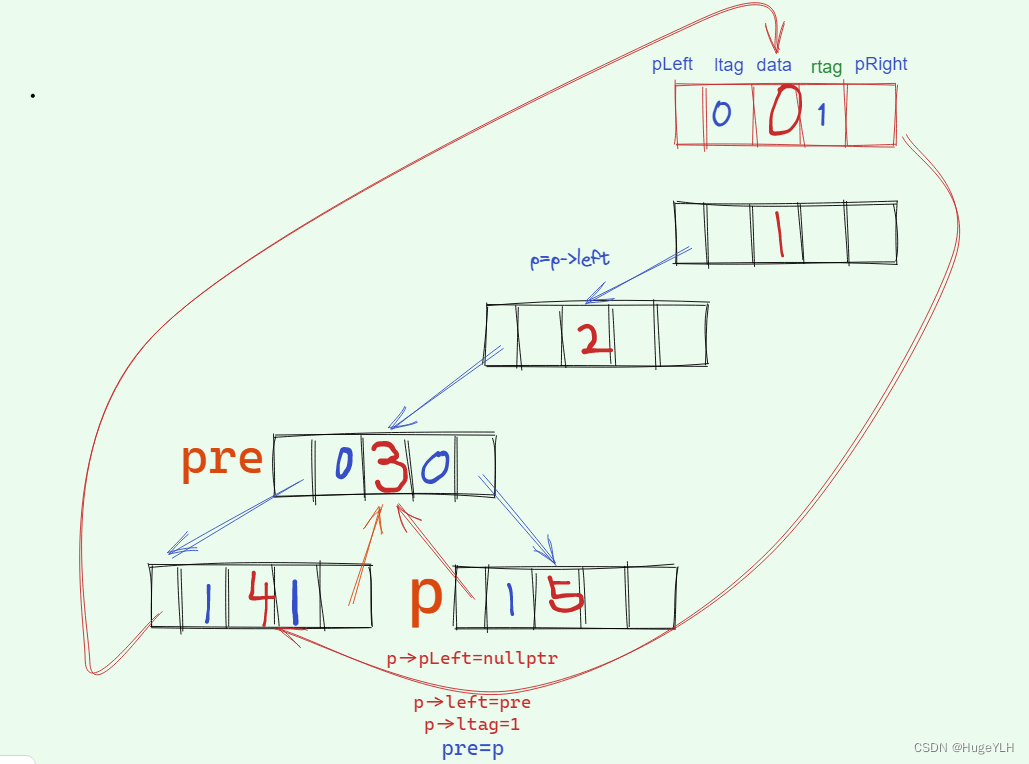
    在这里插入图片描述

  4. 节点5的右指针为空，因此返回递归，到达了节点2，pre指向节点5。节点2的左指针不为空，因此ltag标记0。pre的右指针为空，pre的右指针指向p，rtag标记为1，接着递归进入节点2的右子树，为空，则返回上一层。对于节点5的线索化也完成了！
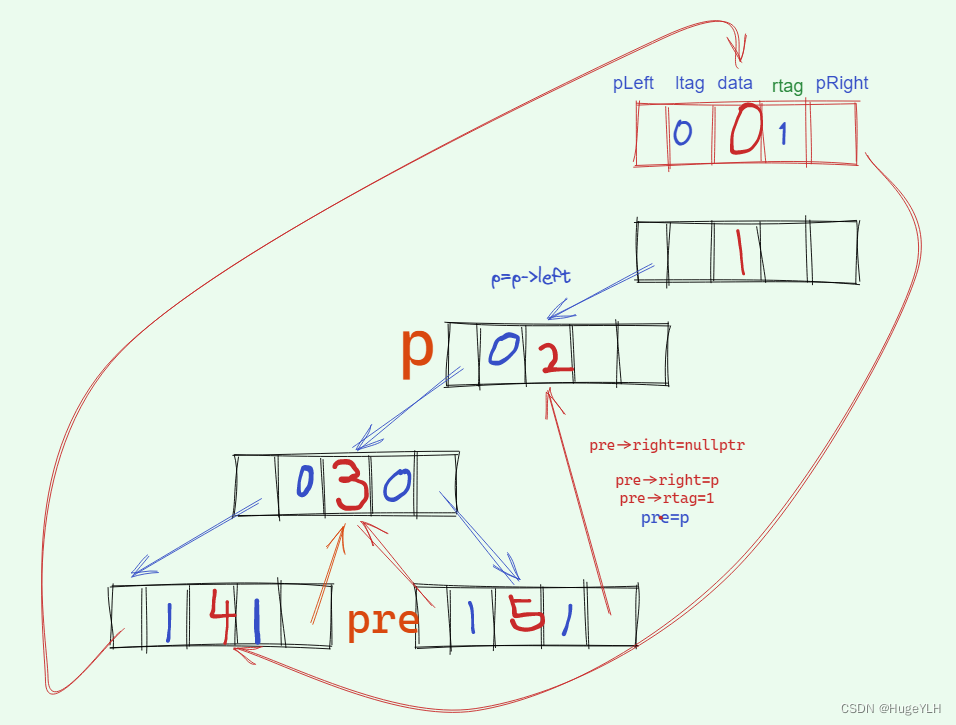
    在这里插入图片描述

  5. p到达节点1，pre到达节点2，p的左指针不为空，无需线索化，ltag标记为0。pre的右指针为空，需要线索化，pre的右指针指向p，rtag标记为1，节点2的线索化就完成了！

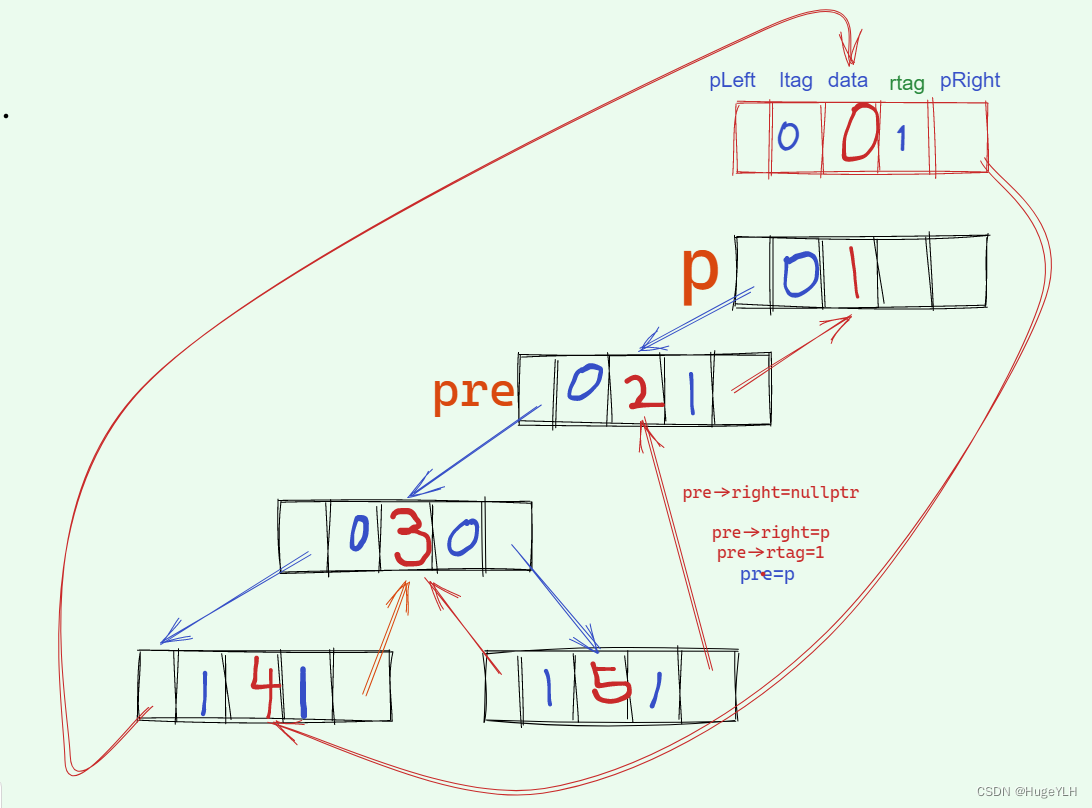
在这里插入图片描述
6. 接下来进入节点1的右子树的递归，为空，所以返回上一层，递归结束，返回到函数中。头节点的右指针连接到pre上，rtag标记为1，根节点的右指针也连接到头节点上，rtag标记为1，此时整棵树的线索化就完成了！

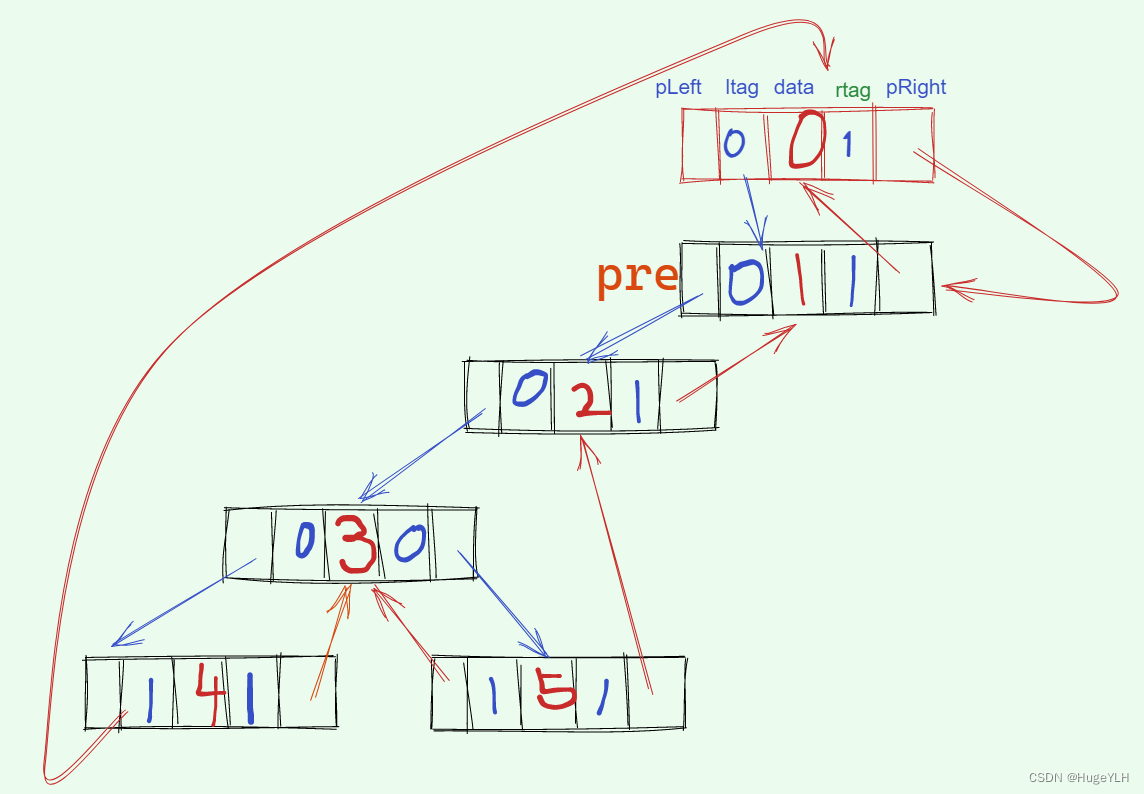
在这里插入图片描述

如何来检测结果的正确性？
中序遍历序列：

4 ---- 3 ----- 5 ----- 2 ------ 1
4的前驱为头节点，后继为节点3。（线索化）
3的前驱为节点4，后继是节点5。（无需线索化）
5的前驱是节点3，后继是节点2。（线索化）
2的前驱是节点5，后继是节点1。（右线索化）
1的前驱是节点2，后继是根节点。（右线索化）
根节点始终与中序遍历的最后一个节点的右指针互相连接。

其他操作

销毁二叉搜索树

如果 ltag和rtag都等于0，表示节点具有左右子树；如果都不等于1，则相当于上面的叶子节点4一样，递归到了树底层，则删除此节点。

template<typename T>
void Tree<T>::_destroyTH(TreeNode<T>*& bt)
{
	//左子树不为空，递归到最后一个左子树叶子节点
	if (bt->ltag == 0)
	{
		_destroyTH(bt->pleft);
	}
	//右子树不为空，递归到最后一个右子树叶子节点
	if (bt->rtag == 0)
	{
		_destroyTH(bt->pright);
	}
	delete bt;
	bt = nullptr;
}

获取中序遍历的第一个节点

当最后一个节点的ltag为1时，则表示到达了最后。

template<typename T>
TreeNode<T>* Tree<T>::FindMidFirst()
{
	TreeNode<T>* begnode = root->pleft;
	while (begnode->ltag == 0)
	{
		begnode = begnode->pleft;
	}
	return begnode;
}

获取中序遍历的最后一个节点

头节点与中序遍历的最后一个节点相互连接，因此它的右指针就是中序遍历的最后一个节点。

template<typename T>
TreeNode<T>* Tree<T>::FindMidLast()
{
	return root->pright;
}

输出中序遍历序列

template<typename T>
TreeNode<T>* Tree<T>::PreNode(TreeNode<T>* p)
{
	auto find = p->pleft;
	if (p->ltag != 1)
	{
		while (find->rtag == 0)
		{
			find = find->pright;
		}
	}
	return find;
}

template<typename T>
void Tree<T>::_midtavel()
{
	TreeNode<T>* node;
	node = FindMidFirst();
	while (node != root)
	{
		cout << node->data << " ";
		node = NextNode(node);
	}
	cout << endl;
}

逆序输出中序遍历序列

template<typename T>
TreeNode<T>* Tree<T>::NextNode(TreeNode<T>* p)
{
	auto find = p->pright;
	if (p->rtag != 1)
	{
		while (find->ltag == 0)
		{
			find = find->pleft;
		}
	}
	return find;
}

template<typename T>
void Tree<T>::_rmidtravel()
{
	auto node = FindMidLast();
	while (node != root)
	{
		cout << node->data << " ";
		node = PreNode(node);
	}
	cout << endl;
}

源码

#include <iostream>
#include <algorithm>
#include <vld.h>
#include <vector>
#include <stack>
#include <list>
using namespace std;

template <typename T>
struct TreeNode
{
	T data;
	TreeNode* pleft, * pright;
	int ltag, rtag;
	TreeNode(const T& data = 0) 
		:data(data), pleft(nullptr), pright(nullptr),rtag(0),ltag(0) {}
	TreeNode(const T& data, TreeNode* pleft, TreeNode* pright, int ltag, int rtag)
		:data(data), pleft(pleft), pright(pright), ltag(ltag), rtag(rtag) {}
};

template <typename T = int>
class Tree
{
public:
	Tree();
	~Tree();
	void CreateTree(const T& val);
	//中序遍历序列
	void MidTravel();
	//逆中序遍历序列
	void rMidTravel();
	void CreateThreadTree();
	void destroyThreadTree();
	void destroyTree();

	//查找中序遍历的第一个节点
	TreeNode<T>* FindMidFirst();
	//得到中序遍历的最后一个节点
	TreeNode<T>* FindMidLast();
private:
	//找P节点的中序前驱节点
	TreeNode<T>* PreNode(TreeNode<T>* p);
	//找P节点的中序后继节点
	TreeNode<T>* NextNode(TreeNode<T>* p);
	void _destroyTree(TreeNode<T>*& bt);
	void _midtavel();
	void _rmidtravel();
	void _createTree(TreeNode<T>*& root,const T& val);
	TreeNode<T>* _createThread_Tree(TreeNode<T>* bt);
	void _Thread(TreeNode<T>*& bt);
	void _destroyTH(TreeNode<T>*& bt);
private:
	TreeNode<T>* root;
	TreeNode<T>* pre;
};

int main()
{
	Tree<> a;
	int arr[]{ 1,2,5,4,1,9 };
	for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
	{
		a.CreateTree(arr[i]);
	}
	a.CreateThreadTree();
	auto beg =  a.FindMidFirst();
	auto end = a.FindMidLast();
	a.MidTravel();
	a.rMidTravel();
	return 0;
}

template<typename T>
Tree<T>::Tree()
{
	root = nullptr;
	pre = nullptr;
}

template<typename T>
Tree<T>::~Tree()
{
	if (pre == nullptr)
	{
		destroyTree();
	}
	else
	{
		destroyThreadTree();
	}
}

template<typename T>
void Tree<T>::CreateTree(const T&val)
{
	_createTree(root, val);
}

template<typename T>
void Tree<T>::MidTravel() 
{
	_midtavel();
}

template<typename T>
void Tree<T>::rMidTravel()
{
	_rmidtravel();
}

template<typename T>
void Tree<T>::CreateThreadTree()
{
	root = _createThread_Tree(root);
}

template<typename T>
void Tree<T>::destroyThreadTree()
{
	auto pNode = root->pleft;		//保存下一个节点的位置
	delete root;	//删除头节点的内存
	root = nullptr;
	_destroyTH(pNode);
	pre = nullptr;
}

template<typename T>
void Tree<T>::destroyTree()
{
	_destroyTree(root);
	root = nullptr;
}

template<typename T>
TreeNode<T>* Tree<T>::FindMidFirst()
{
	TreeNode<T>* begnode = root->pleft;
	while (begnode->ltag == 0)
	{
		begnode = begnode->pleft;
	}
	return begnode;
}

template<typename T>
TreeNode<T>* Tree<T>::FindMidLast()
{
	return root->pright;
}

template<typename T>
TreeNode<T>* Tree<T>::PreNode(TreeNode<T>* p)
{
	auto find = p->pleft;
	if (p->ltag != 1)
	{
		while (find->rtag == 0)
		{
			find = find->pright;
		}
	}
	return find;
}

template<typename T>
TreeNode<T>* Tree<T>::NextNode(TreeNode<T>* p)
{
	auto find = p->pright;
	if (p->rtag != 1)
	{
		while (find->ltag == 0)
		{
			find = find->pleft;
		}
	}
	return find;
}

template<typename T>
void Tree<T>::_destroyTree(TreeNode<T>*& bt)
{
	if (bt != nullptr)
	{
		_destroyTree(bt->pleft);
		_destroyTree(bt->pright);
		delete bt;
	}
}

template<typename T>
void Tree<T>::_midtavel()
{
	TreeNode<T>* node;
	node = FindMidFirst();
	while (node != root)
	{
		cout << node->data << " ";
		node = NextNode(node);
	}
	cout << endl;
}

template<typename T>
void Tree<T>::_rmidtravel()
{
	auto node = FindMidLast();
	while (node != root)
	{
		cout << node->data << " ";
		node = PreNode(node);
	}
	cout << endl;
}

template<typename T>
void Tree<T>::_createTree(TreeNode<T>*& root, const T& val)
{
	if (root == nullptr)
	{
		root = new TreeNode<T>{ val };
		return;
	}
	if (val <= root->data)
	{
		_createTree(root->pleft, val);
	}
	else
	{
		_createTree(root->pright, val);
	}
}

template<typename T>
TreeNode<T>* Tree<T>::_createThread_Tree(TreeNode<T>* bt)
{
	//增加一个头节点
	TreeNode<T>* pHead = new TreeNode<T>{ 0,nullptr,bt,0,1 };
	if (bt == nullptr)
	{
		pHead->ltag = 0;
		pHead->pleft = pHead;
		pHead->rtag = 1;
		pHead->pright = nullptr;
	}
	else
	{
		//bt不为空树
		pHead->pleft = bt;
		pre = pHead;			//前驱节点默认为头节点
		_Thread(bt);	//线索连接
		//结束后，pre指向根节点  进行头节点根节点的连接
		pHead->pright = pre;	
		pre->pright = pHead;
		pre->rtag = 1;				
	}
	//返回头节点
	return pHead;
}

template<typename T>
void Tree<T>::_Thread(TreeNode<T>*& bt)
{	
	if (bt != nullptr)
	{
		_Thread(bt->pleft);	//递归进入右子树，开始线索化
		//线索化
		if (bt->pleft == nullptr)
		{
			bt->pleft = pre;
			bt->ltag = 1;
		}
		else
		{
			bt->ltag = 0;
		}
		if (pre->pright == nullptr)
		{
			pre->pright = bt;
			pre->rtag = 1;
		}
		else
		{
			pre->rtag = 0;
		}
		//node.emplace_back(bt);
		pre = bt;
		_Thread(bt->pright);	//递归进入右子树，开始线索化
	}
}

template<typename T>
void Tree<T>::_destroyTH(TreeNode<T>*& bt)
{
	//左子树不为空，递归到最后一个左子树叶子节点
	if (bt->ltag == 0)
	{
		_destroyTH(bt->pleft);
	}
	//右子树不为空，递归到最后一个右子树叶子节点
	if (bt->rtag == 0)
	{
		_destroyTH(bt->pright);
	}
	delete bt;
	bt = nullptr;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/52024.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Linux零基础入门（一）初识Linux

Linux零基础入门（一）初识Linux

Linux零基础入门&#xff08;一&#xff09;初识Linux前言操作系统概述一 操作系统概述1 硬件和软件2 操作系统二 初识Linux1 Linux的诞生2 Linux内核3 Linux发行版三 虚拟机介绍1 虚拟机四 VMware WorkStation安装1 虚拟化软件五 在VMware上安装Linux1 下载CentOS操作系统六 远…
阅读更多...
[附源码]计算机毕业设计springboot体育馆场地预约管理系统

[附源码]计算机毕业设计springboot体育馆场地预约管理系统

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
SwiftUI 如何快速识别视图（View）界面的刷新是由哪个状态的改变导致的？

SwiftUI 如何快速识别视图（View）界面的刷新是由哪个状态的改变导致的？

功能需求 在 SwiftUI 中，我们视图的界面可能在不经意间被意外刷新了。这时，我们希望知道是该视图中的哪个状态导致了刷新。在包含众多状态的复杂视图中，这往往很难实现。 如上图所示，当我们随机改变视图中的状态时，可以在调试控制台中轻松看到是哪个状态导致了视图的刷新…
阅读更多...
什么样的跨网数据摆渡系统，能够减少数据泄密的风险？

什么样的跨网数据摆渡系统，能够减少数据泄密的风险？

企业在公司正常运行下难免会产生一些重要数据或者敏感数据&#xff0c;这些都是企业在发展过程中积累下来的重要数据资产&#xff0c;对企业的发展至关重要。这些数据资产往往关联着企业的核心数据&#xff0c;一旦面临泄露&#xff0c;不仅仅会影响企业发展&#xff0c;甚至会…
阅读更多...
词法分析（编译原理不用慌）

词法分析（编译原理不用慌）

目录 一.简单版 二.简单版&#xff08;文本保存&#xff09; c版 运行结果&#xff1a; Java版 运行结果&#xff1a; 三.第三版&#xff08;文本保存&#xff09; c版 运行结果&#xff1a; 一.简单版 #include<stdio.h> #include<iostream> using namesp…
阅读更多...
独立站SaaS系统站群模式怎么玩

独立站SaaS系统站群模式怎么玩

做独立站的人都知道“站群”这个游戏&#xff0c;意思是通过建站工具一次性建好几百个或者几千个独立站。各个独立站卖的品类比较垂直&#xff0c;不会有太多SKU。销量好的站会留着精细化运营&#xff0c;没流量的就放弃。 使用脸书或谷歌和其他广告渠道来测试产品。每个产品…
阅读更多...
Unity3d bounds包围盒 和collider碰撞器区别

Unity3d bounds包围盒 和collider碰撞器区别

Bounds 外包围盒 Bounds 叫作外包围盒、边界框、外扩矩形.是struct 结构体。而我们获得Bounds的主要途径有三种&#xff1a;Render,Collider,Mesh。 Render.bounds 世界坐标 Collider.bounds 世界坐标 Mesh.bounds 本地坐标 var m GetComponent<MeshFilter>().bound…
阅读更多...
抖音用户浏览行为数据分析与挖掘

抖音用户浏览行为数据分析与挖掘

下文部分代码省略&#xff0c;完整项目代码及数据集链接&#xff1a;抖音用户浏览行为数据分析与挖掘 目录1.特征指标构建0. 项目介绍与说明**数据集说明**浏览行为1. 数据简单处理2. 特征指标构建用户指标分析&#xff1a;作者指标分析&#xff1a;作品指标分析&#xff1a;3.…
阅读更多...
5分钟快速上手Nmap指令（基于Kali系统）

5分钟快速上手Nmap指令（基于Kali系统）

前言正文1、修改Kali系统中网络配置2、Nmap简介2.1 用途2.2优势2.3 相关知识3、Nmap中最常用的命令3.1 单主机扫描3.2 多目标扫描3.3 检测目标主机漏洞3.3 时序选择3.4 保存4、kali系统中常见报错参考文献前言 本篇为理论篇&#xff0c;主要为CTF攻防做铺垫&#xff0c;围绕 基…
阅读更多...
[附源码]SSM计算机毕业设计影院售票系统JAVA

[附源码]SSM计算机毕业设计影院售票系统JAVA

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
mac m1 mysqlworkbench8 Unknown table ‘COLUMN_STATISTICS‘

mac m1 mysqlworkbench8 Unknown table ‘COLUMN_STATISTICS‘

原因&#xff1a;本地mysql版本是8&#xff0c;远程是mariaDb-10&#xff0c;版本不匹配导致报错。 仔细看mysqlworkbench8.0导出时的错误信息&#xff0c;有mysqldump的具体路径。 mac os (m1, ventura系统)&#xff0c;具体位置是这里&#xff1a; /Applications/MySQLWor…
阅读更多...
【树莓派开发日记1】1.3k预算的树莓派+显示屏+键鼠的选型与拆箱物理安装

【树莓派开发日记1】1.3k预算的树莓派+显示屏+键鼠的选型与拆箱物理安装

树莓派开发日记1 经过了漫长的上课与考试周期&#xff0c;终于有时间闲下来进行技术栈的开发与学习 作为立志成为优秀机器人开发者的青年工程师&#xff08;青春版&#xff09;&#xff0c;不可能不去了解微机处理系统和Ubuntu系统&#xff0c;所以在此又给自己开了一个大坑 …
阅读更多...
OpManager 帮助排查网络延迟问题

OpManager 帮助排查网络延迟问题

什么是网络延迟 网络中的延迟是指数据通过网络传输到其预期目的地所需的时间。它通常表示为往返延迟&#xff0c;即数据从一个位置传输到另一个位置所需的时间。 什么原因导致网络延迟 有四个主要原因会影响网络延迟。其中包括&#xff1a; 传输介质&#xff0c;例如 WAN 或…
阅读更多...
JUC并发编程第六篇，带你了解Java内存模型JMM

JUC并发编程第六篇，带你了解Java内存模型JMM

JUC并发编程第六篇&#xff0c;带你了解Java内存模型JMM一、Java Memory Model&#xff08;Java内存模型&#xff09;是什么&#xff1f;二、JMM规范三大特性1. 可见性2. 原子性3. 有序性三、JMM规范下多线程对变量的读写过程四、JMM规范下多线程先行发生原则&#xff08;happe…
阅读更多...
Oracle面试题整理

Oracle面试题整理

目录 Oracle面试题整理 1.MySQL和Oracle的区别&#xff1a; 2.Oracle中function和procedure的区别&#xff1f; 3. 比较truncate和delete命令 &#xff1f; 4.oralce中 rowid, rownum的定义 5. 事务的特性&#xff08;ACID&#xff09;是指什么 6. 列举几种表连接方式…
阅读更多...
[附源码]计算机毕业设计springboot天狗电子商城系统

[附源码]计算机毕业设计springboot天狗电子商城系统

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
plink2.0和plink1.9的忧伤笔记

plink2.0和plink1.9的忧伤笔记

虽然plink2.0已经存在好久了&#xff0c;但是一直用的都是plink1.9&#xff0c;因为语法熟悉。更主要是plink2.0语法变动太大&#xff0c;害怕步子迈得太大了…… 今天看一下plink2.0的读入和输出数据常用参数&#xff0c; plink2.0用是不会用的&#xff0c;2022年都不会用&am…
阅读更多...
计算机网络基础

计算机网络基础

前言 计算机网络学习的核心内容就是网络协议的学习。网络协议是为计算机网络中进行数据交换而建立的规则、标准或者说是约定的集合。因为不同用户的数据终端可能采取的字符集是不同的&#xff0c;两者需要进行通信&#xff0c;必须要在一定的标准上进行。一个很形象地比喻就是…
阅读更多...
平时健身买什么耳机好、分享五款最好的运动耳机推荐

平时健身买什么耳机好、分享五款最好的运动耳机推荐

不少人喜欢在健身房或者户外运动中使用手机或者MP3来听音乐&#xff0c;这种方式不仅可以减少运动中的枯燥感&#xff0c;而且那些节奏较强的音乐还能够进一步激发人们的运动潜能&#xff0c;达到事半功倍的效果。作为音乐传递的桥梁&#xff0c;一款佩戴舒适的运动耳机是必不可…
阅读更多...
又撸了一个开源项目！！！

又撸了一个开源项目！！！

花了两周左右&#xff0c;写了一个客户关系管理系统&#xff0c;基于 Vue Go 实现&#xff0c;主要功能有仪表盘、客户管理、合同管理、产品管理&#xff0c;订阅等功能。 前几天已经在 Github 上开源了&#xff0c;今天也把项目部署到云服务器上了&#xff0c;很完美&#x…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023