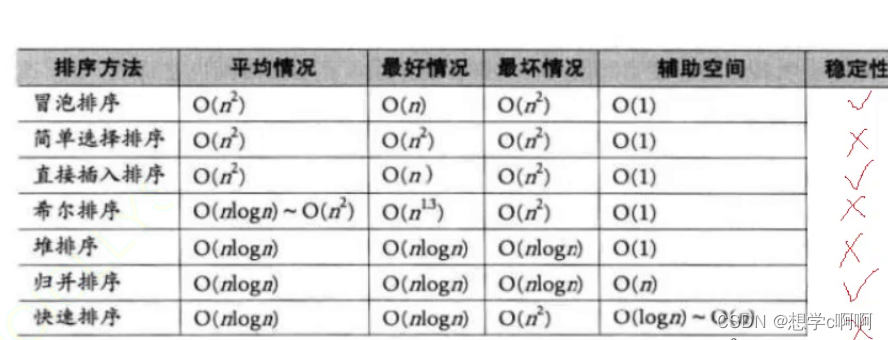
常见八种排序实现方法
- 前言
- 快速排序
- 堆排序
- 冒泡排序
- 代码
- 选择排序
- 代码部分
- 插入排序
- 思路讲解
- 代码部分
- 希尔排序
- 代码部分
- 思路讲解
- 归并排序
- 递归
- 思路讲解
- 代码部分
- 非递归
- 梭哈
- 代码部分
- 思路讲解
- 非梭哈
- 代码部分
- 计数排序
- 代码部分
前言
这里的快速排序和堆排序博主以前都写过,这里就直接附上链接了
这篇博客后,就准备去狂补c艹和linux的内容了。
快速排序
给个以前博客就摸了
堆排序
不是我想摸,只是因为以前写的比较详细
冒泡排序
这个想必是所有人接触到的第一个排序方法
原理和过程也是十分容易理解

这里只需要不停比较交换就可
这里就不细讲这个排序了,想必现在兄弟们看它就像看亲人一样亲
代码
void buddle_sort(int* arr, int arrsize)
{
for (int i = 0; i < arrsize; i++)
{
//这里稍微优化了一下,循环几次,最后几位肯定是最大值,直接-i即可
for (int g = 0; g < arrsize - i-1; g++)
{
if (arr[g] > arr[g + 1])
{
int tmp = arr[g + 1];
arr[g + 1] = arr[g];
arr[g] = tmp;
}
}
}
}
但是这个老亲人唯一的意义可能就是教学意义了,本身在O(n^2)的排序排序中也只能算上一个弟中之弟了。
选择排序

这里是我们最简单的选择排序,首先对整个数组进行遍历,找到最小值后,对左边的值进行交换
我们就不写这个最简单的写法了,这里还有一种优化方式
遍历整个数组,同时找到最大值和最小值,将最大值放在右边,将最小值放在左边.
代码部分
void swap(int* arr, int x, int y)
{
int tmp = arr[x];
arr[x] = arr[y];
arr[y] = tmp;
}
void select_sort(int* arr, int arrsize)
{
int begin = 0, right = arrsize-1;
while (begin <right)
{
int max = begin;
int mix = begin;
for (int i = begin; i <= right; i++)
{
if (arr[i] < arr[mix])
{
mix = i;
}
if (arr[i] > arr[max])
{
max = i;
}
}
swap(arr, begin, mix);
swap(arr, right, max);
begin++;
right--;
}
}
插入排序

这个可以算是O(N^2) 量级的排序的神了.
思路讲解
说简单一点,就是将第i个数字与i前面的有序数组的元素按顺序进行比较
(以升序为准)
如果i元素大于i+1元素,则将arr[i]=arr[i+1]
因为这里我们事先将i元素值记录了下来,所以这里直接覆盖就好
如果i元素小于等于i+1元素,则将i值赋值到当前位置,停止比较
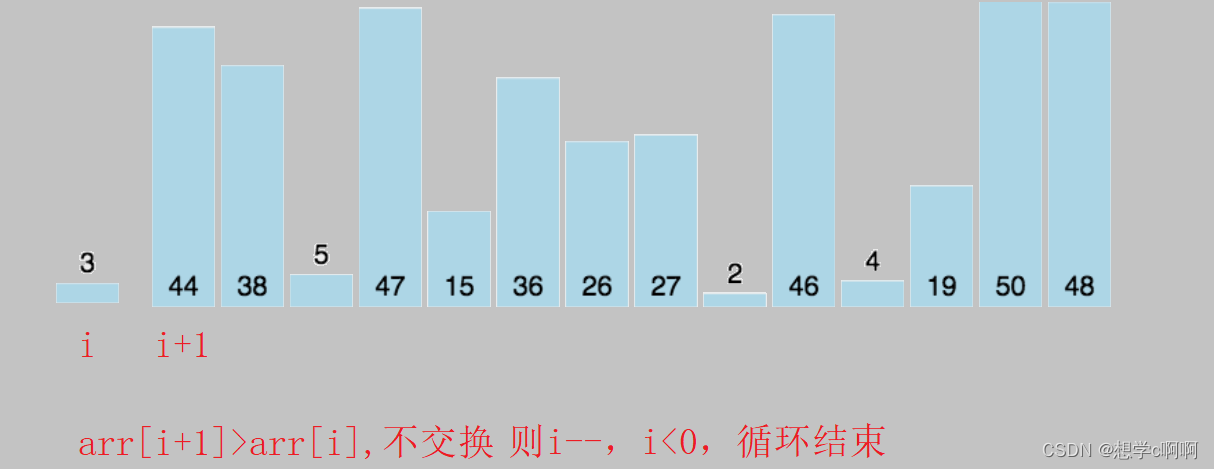
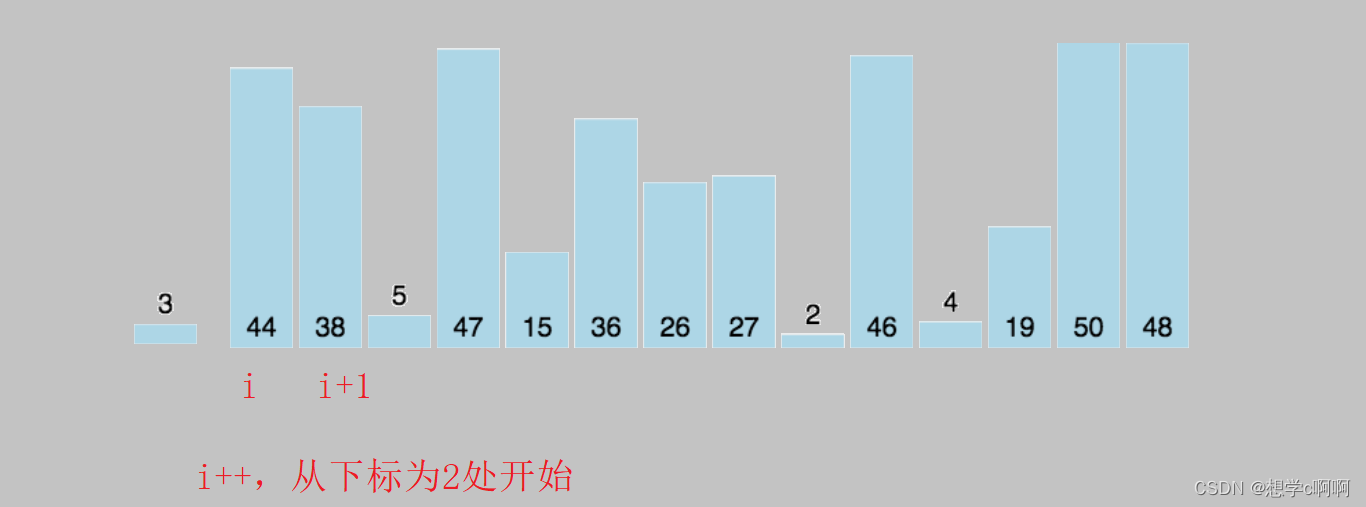
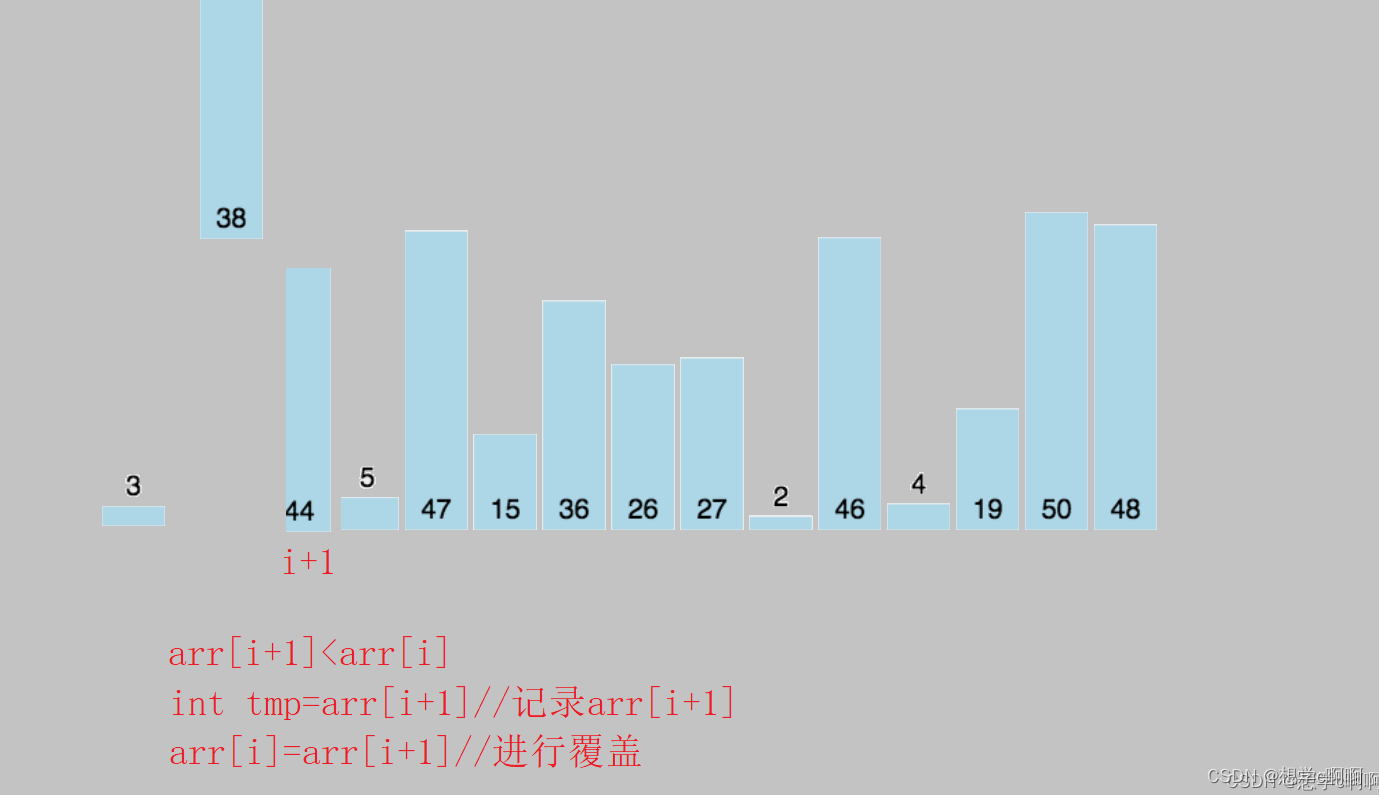
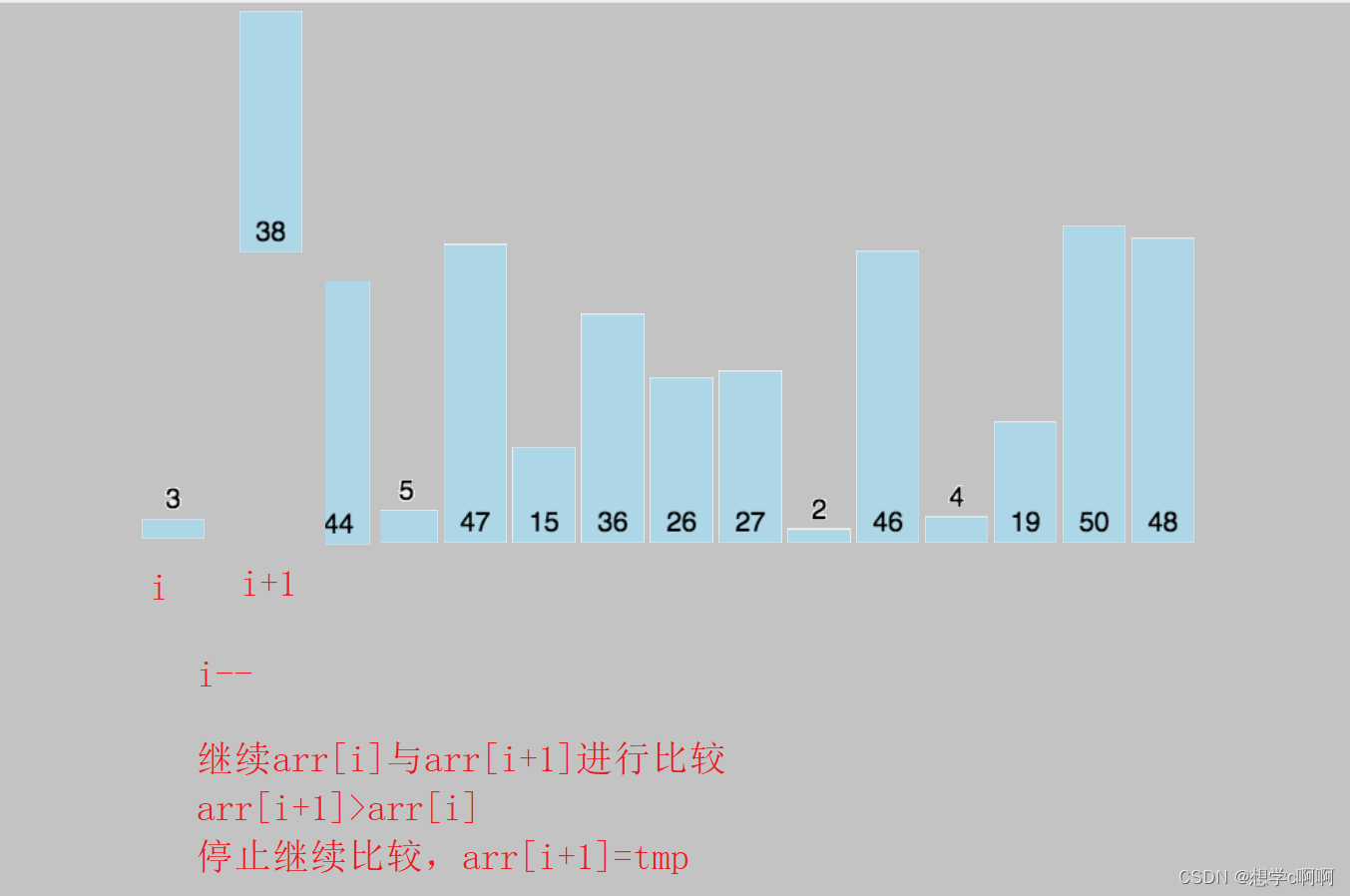
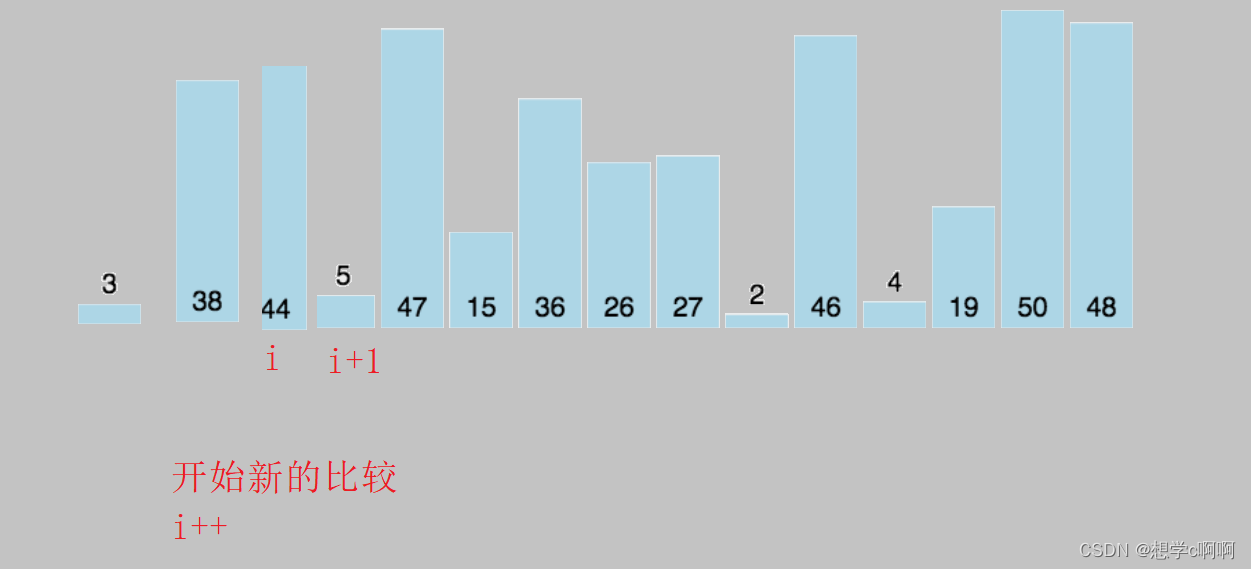
到这里单次排序的规则已经明了
代码部分
void insert_sort(int* arr, int arrsize)
{
for (int i = 1; i < arrsize; i++)
//对所有数进行遍历
{
int key = arr[i];
int k = i - 1;
while (k >= 0)
//将k插入到k前面的有序数列
{
if (key < arr[k])
{
arr[k + 1] = arr[k];
k--;
}
else
//找到了正确位置,可以不用再向前走
break;
}
//将key值放到合理的位置
arr[k + 1] = key;
}
}
通过对它的了解,我们知道
如果一开始i与i前面的有序数列刚好成有序
那就可以进行一次比较即可
就是说,越接近有序的数组,对插入排序来说是效率越高的.
如果是一个有序数组,插入排序每次就需要一次比较即可.
那效率将会是O(N)
希尔排序
希尔排序就是建立在插入排序越接近有序的数组,对插入排序来说是效率越高的优点上进行建立的
既然插入排序对有序数组效率这么高
那我们就让一个数组排序到接近有序的状态
然后用插入排序不就能提高的效率了嘛

代码部分
这里先上代码,然后用代码进行讲解.
void shell_sort(int* arr, int arrsize)
{
int gap=arrsize;
while (gap > 1)
{
gap /= 2;
for (int i = gap; i < arrsize; i+=gap)
{
int k=i-gap;
int key=arr[i];
while (k >= 0)
{
if (key < arr[k])
{
arr[k + gap] = arr[k];
k -= gap;
}
else
break;
}
arr[k + gap] = key;
}
}
}
思路讲解
这里先看里面的循环方式.
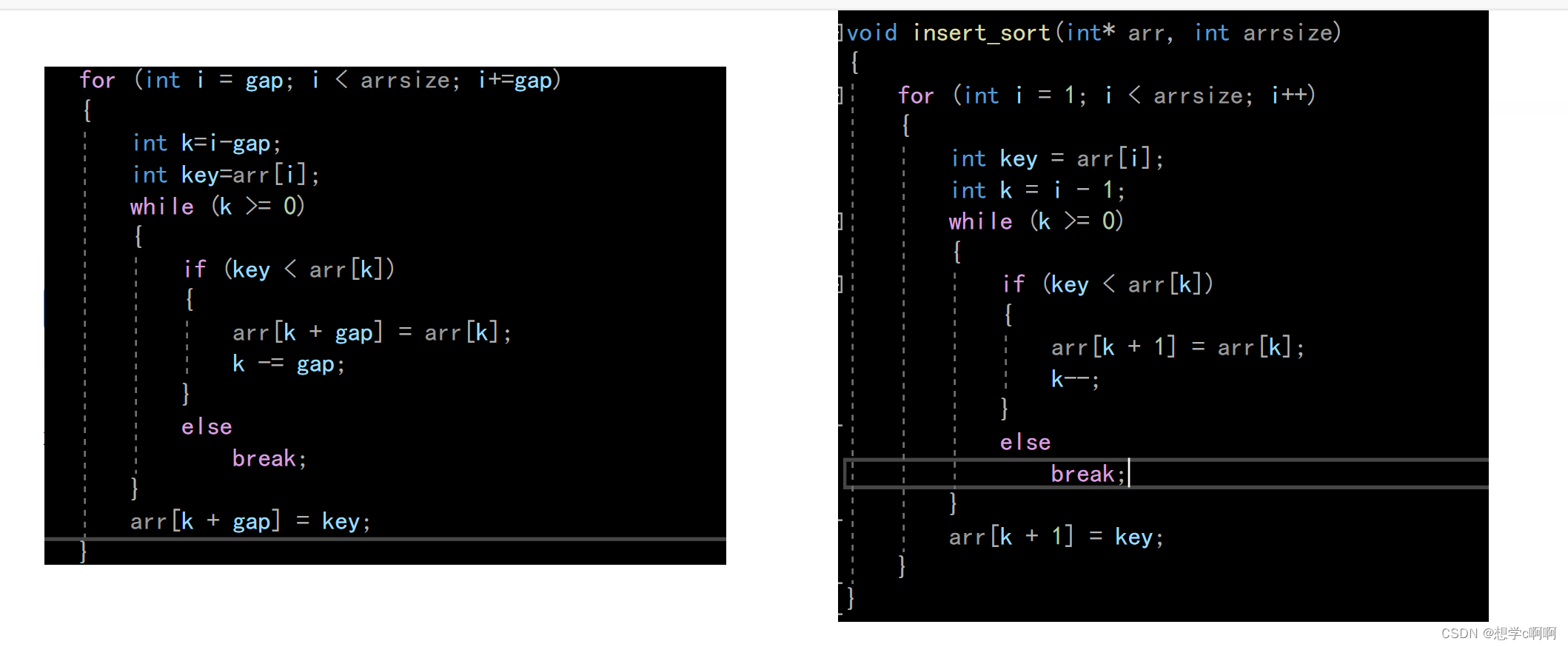
这里截图进行了希尔排序和插入排序的对比,我们就可以发现
两者其实之间就是差了一个gap的值。
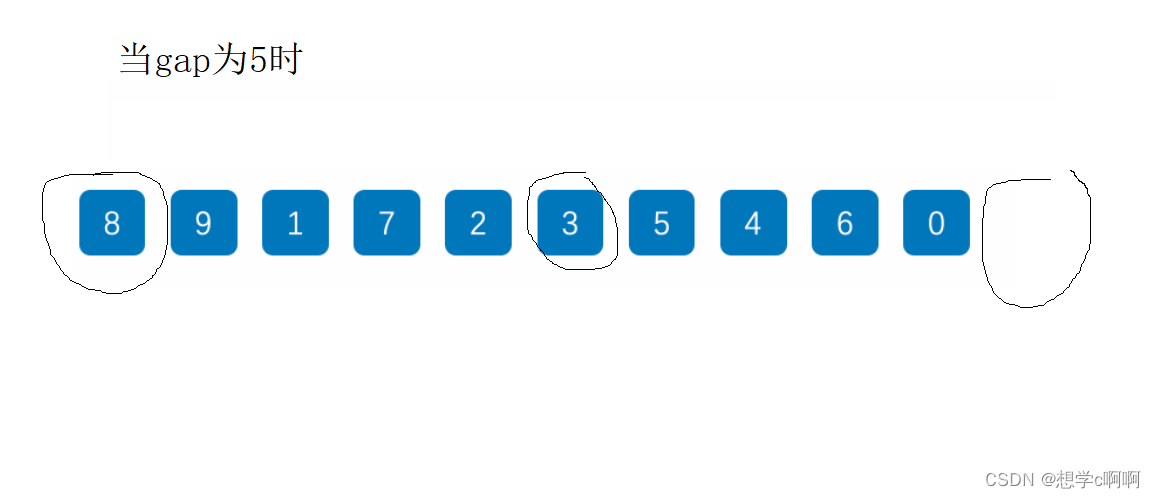
当把gap的值赋5时,插入排序就会对间隔五个的数进行插入排序。
这里我们就能知道,希尔排序为了让数组更有序
就是先对隔了gap个数字的数组先进行插入排序
也就是说,当gap为1时,其与正常的插入排序没有区别
这样的话我们取值gap就可以让gap从一个小于arrsize的值不停变小至1即可。
int gap=arrsize;
while (gap > 1)
{
gap/=2;
//隔gap的排序
{
}
}
这里我们对gap的取值就是
5 2 1
对gap不停/=2,保证gap一定能等于1
就是说整个过程:
1:对 arr[0] arr[5]进行插入排序(gap为5)
2:对 arr[0] arr[2] arr[4] arr[6] arr[8]进行插入排序(gap为2)
3:就是整体的插入排序(gap为1)
归并排序
递归
思路讲解
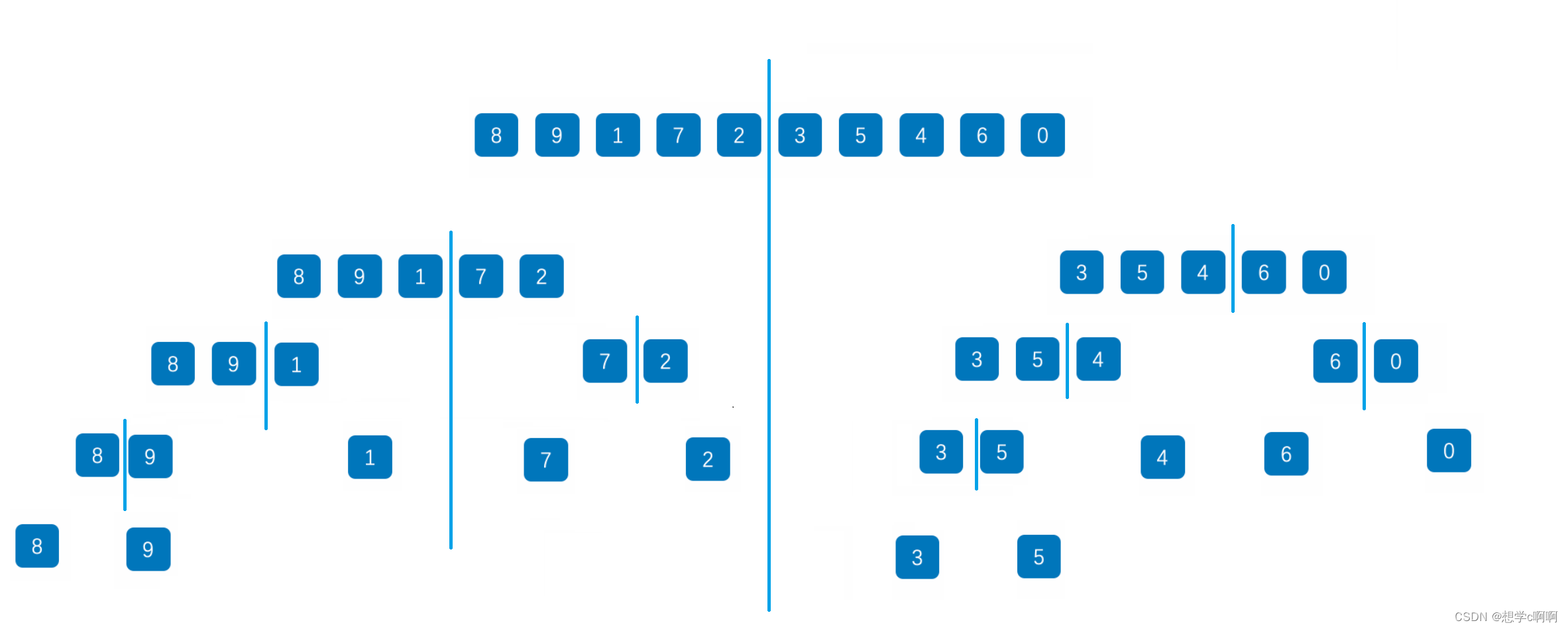
归并就是先将数组分成最小的部分,然后进行两个有序数组的合并
这里先将所有数分成单独的个体,然后进行两个数的合并
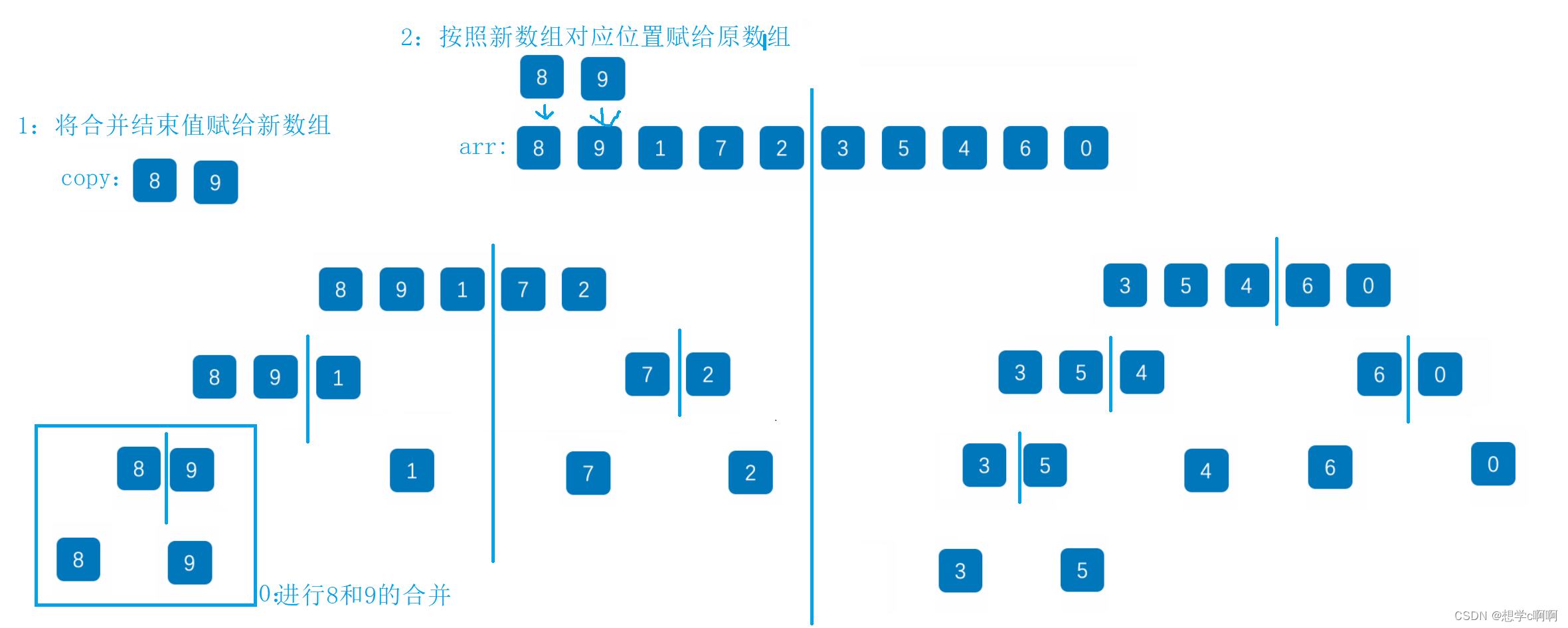
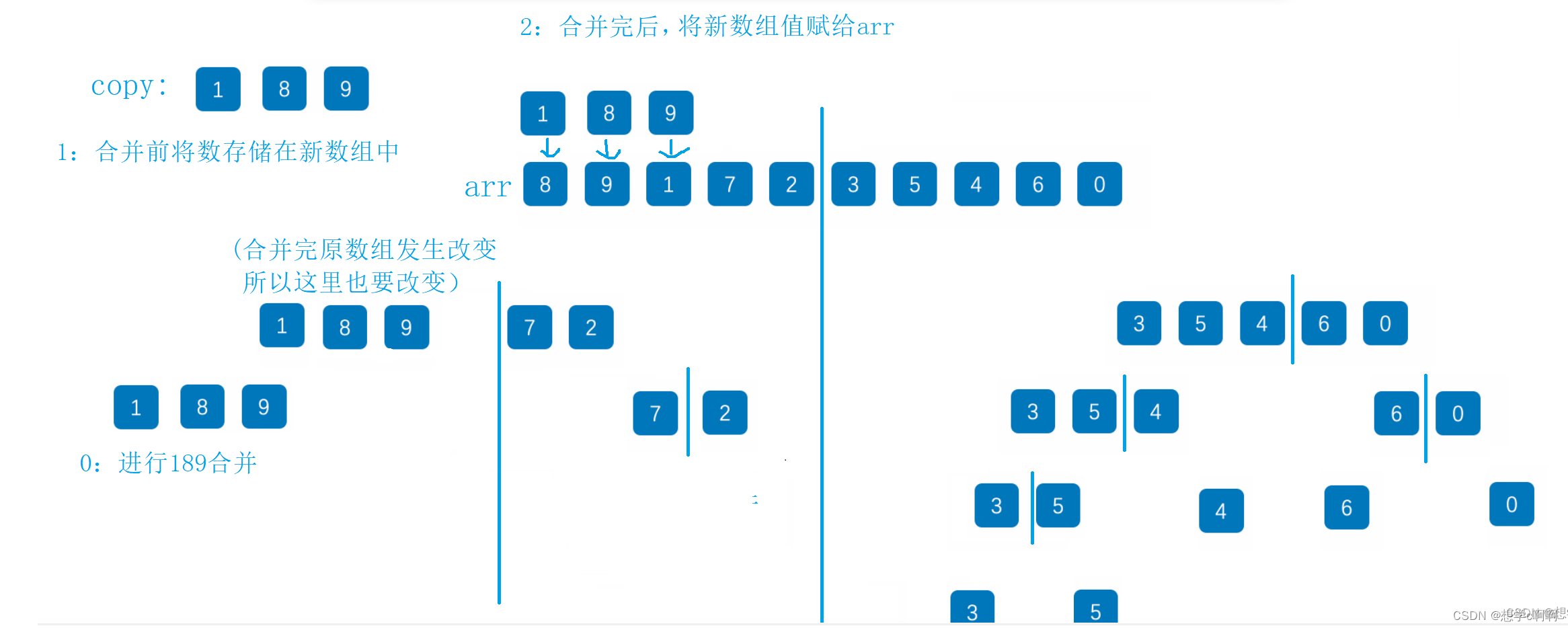
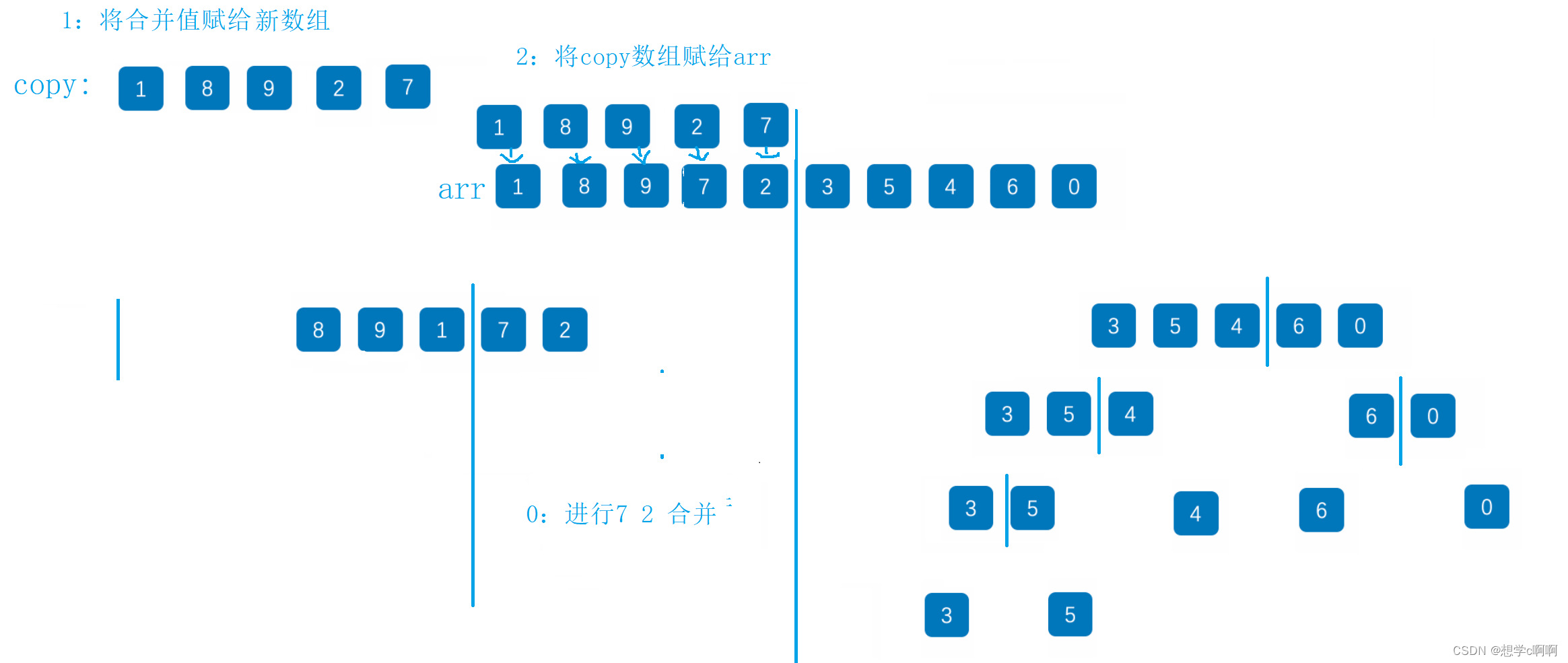
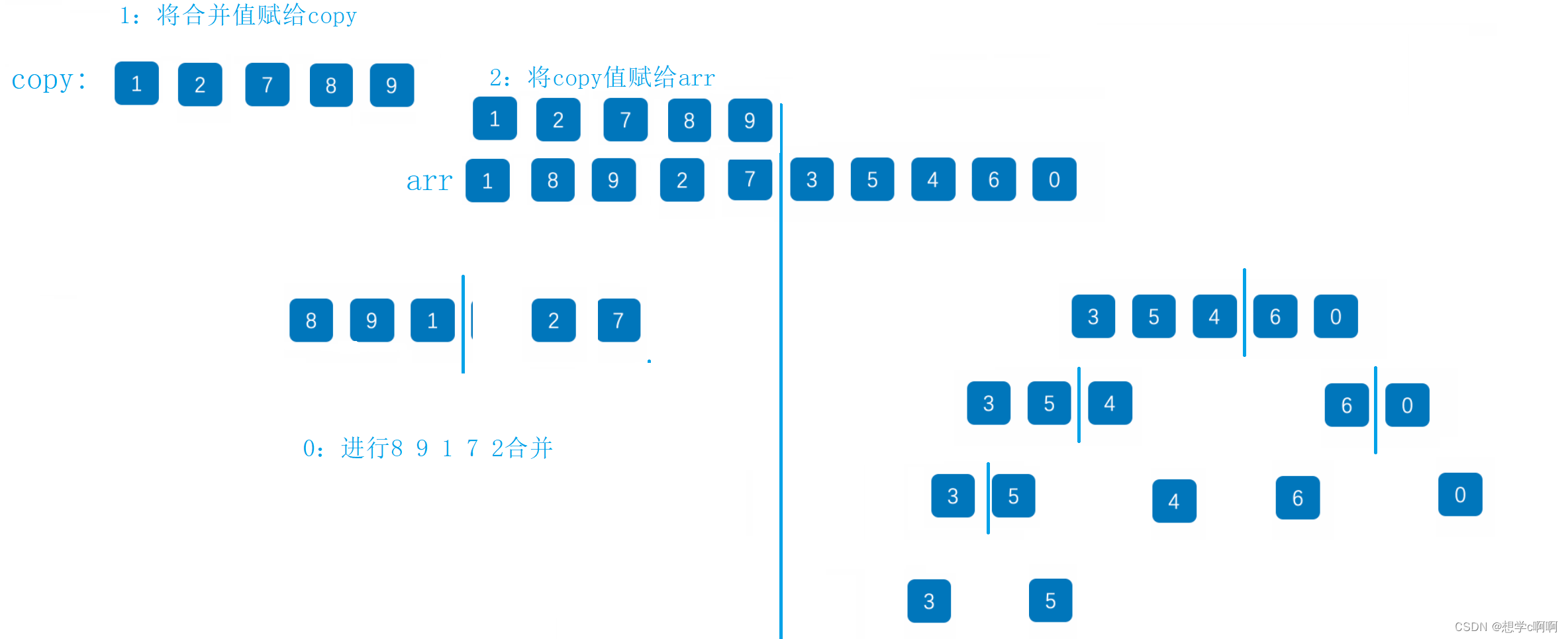
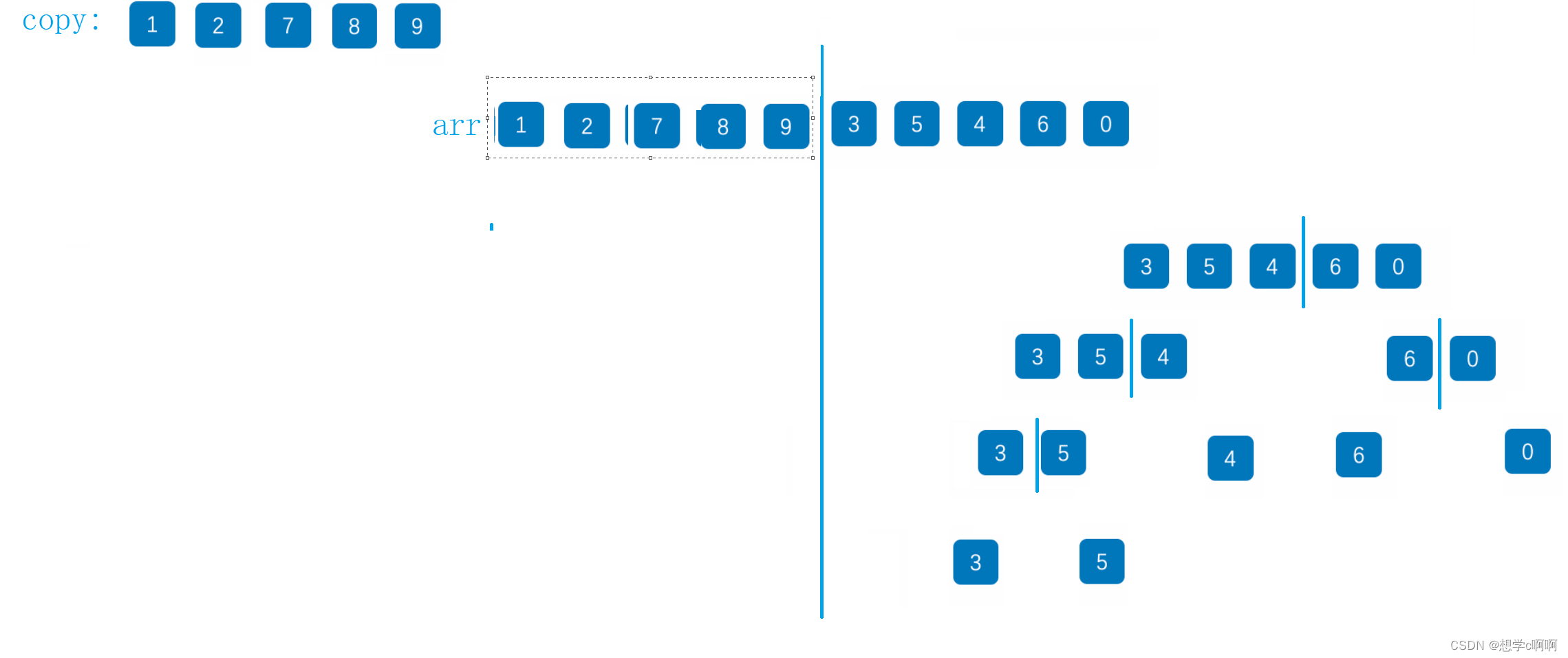
带大家走完了左边部分的归并,右边也同理,就不画了
代码部分
void _merge_sort(int* arr,int left,int right,int* copy)
{
//递归返回条件
if (left >= right)
return;
//数组划分中间坐标
int mid = (left + right) / 2;
//后根遍历,划分到最小后进行操作
_merge_sort(arr, left, mid, copy);
_merge_sort(arr, mid + 1, right, copy);
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int i = left;
//将两个数组挑选数赋值到copy数组
while (begin1 <= end1 && begin2 <= end2)
{
//将两个数组中最小的数放入其中
if (arr[begin1] > arr[begin2])
{
copy[i++] = arr[begin2++];
}
else
{
copy[i++] = arr[begin1++];
}
}
//防止有数组没有将数全部录入
//因为上面的条件是&&
while (begin1 <= end1)
copy[i++] = arr[begin1++];
while (begin2 <= end2)
copy[i++] = arr[begin2++];
//将copy数组的数赋到arr中
for (int i = left; i <= right; i++)
{
arr[i] = copy[i];
}
}
//因为要创建新数组,所以要有两个函数
void merge_sort(int* arr,int arrsize)
{
//创建新数组
int* ptr = (int*)malloc(sizeof(int) * arrsize);
assert(ptr);
_merge_sort(arr, 0, arrsize-1, ptr);
}
非递归
这里是老传统了,为了防止递归使栈溢出
所以就要改成非递归形式
梭哈
这里的梭哈就是取决于
我们什么时候将复制好的数组全部覆盖给原数组
如果是将全部合并好的数组一次性复制给原数组
就是梭哈
如果是合并一部分,复制一部分
就是非梭哈
上面我们的递归思想就是非梭哈
代码部分
void merge_sort_unrecursion_all_in(int* arr,int arrsize)
{
//创建新数组
int* copy = (int*)malloc(sizeof(int) * arrsize);
assert(copy);
int left = 0;
int right = arrsize;
//运用gap来进行归并数组范围的调控
int gap = 1;
while (gap < right)
{
for (int i = 0; i < right; i += gap * 2)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = gap * 2 + i - 1;
int g = i;
//越界后的边界处理
if(end1>right)
{
end1 = right - 1;
begin2 = right;
end2 = right - 1;
}
else if (begin2>right)
{
begin2=right;
end2 = right-1;
}
else if (end2 > right)
{
end2 = right-1;
}
//正常的递归选数复制
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] > arr[begin2])
{
copy[g++] = arr[begin2++];
}
else
{
copy[g++] = arr[begin1++];
}
}
while (begin1 <= end1)
copy[g++] = arr[begin1++];
while (begin2 <= end2)
copy[g++] = arr[begin2++];
}
gap *= 2;
//归并后将数组完全打印到老数组中
for (int g = 0; g <= right-1; g++)
{
arr[g] = copy[g];
}
}
}
思路讲解
这里直接继续用画图来解决思路
同样也是先放上代码进行讲解
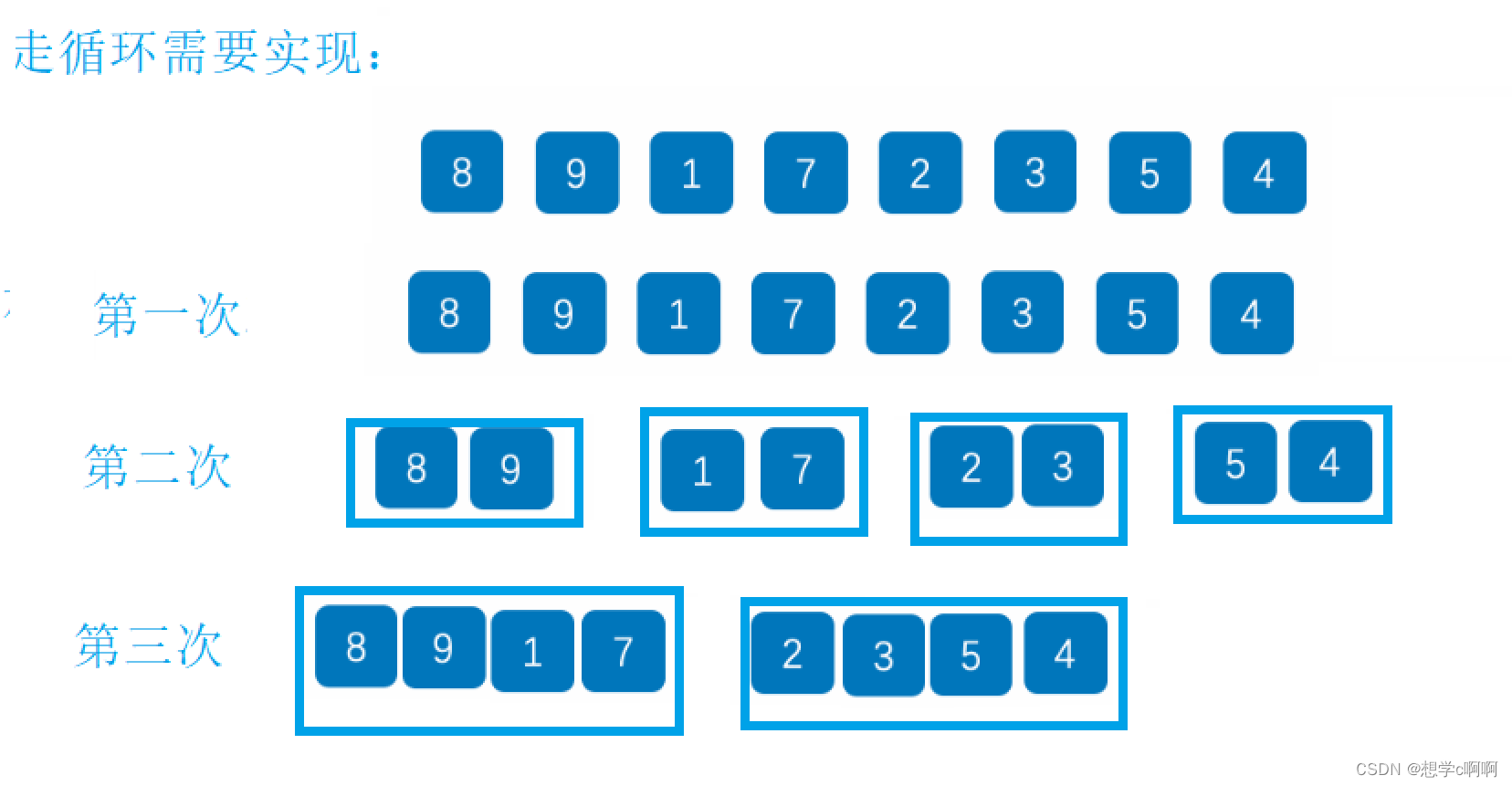
这里可能就有人看出来了,这就是再模仿递归的过程
为了用循环实现这个效果,就使用了gap这个变量
int* copy = (int*)malloc(sizeof(int) * arrsize);
assert(copy);
int left = 0;
int right = arrsize;
int gap = 1;
while (gap < right)
{
for (int i = 0; i < right; i += gap * 2)
{
//这个gap实现了begin1 end1
//begin2 end2 的类递归方式
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = gap * 2 + i - 1;
int g = i;
//{
//递归代码(和递归很像所以略)
//}
//------------------------------------------------
//将全部归并好后,进行gap调整和归并
gap *= 2;
for (int g = 0; g <= right-1; g++)
{
arr[g] = copy[g];
}
}
}
接下来是最重要的部分
if(end1>right)
{
end1 = right - 1;
begin2 = right;
end2 = right - 1;
}
else if (begin2>right)
{
begin2=right;
end2 = right-1;
}
else if (end2 > right)
{
end2 = right-1;
}
请问这个是干嘛用的?
这里我们还是要回到这个gap了
gap *= 2;这里的gap是*=2
当arrsize不是2方的倍数时
如果没有上面这个代码,那会发生什么
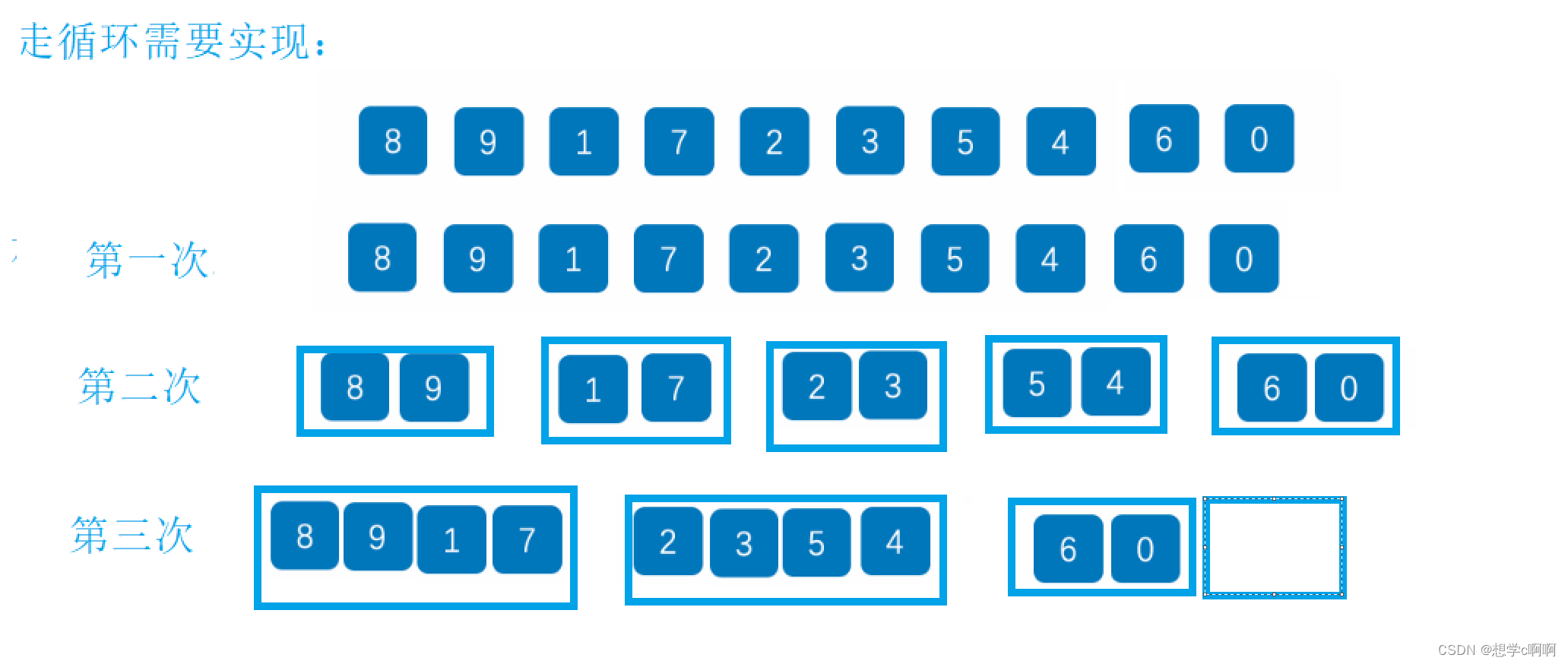
从这个图这里我们就发现,这样会发生非法访问
所以当我们进行排序的时候就需要进行边界调整。
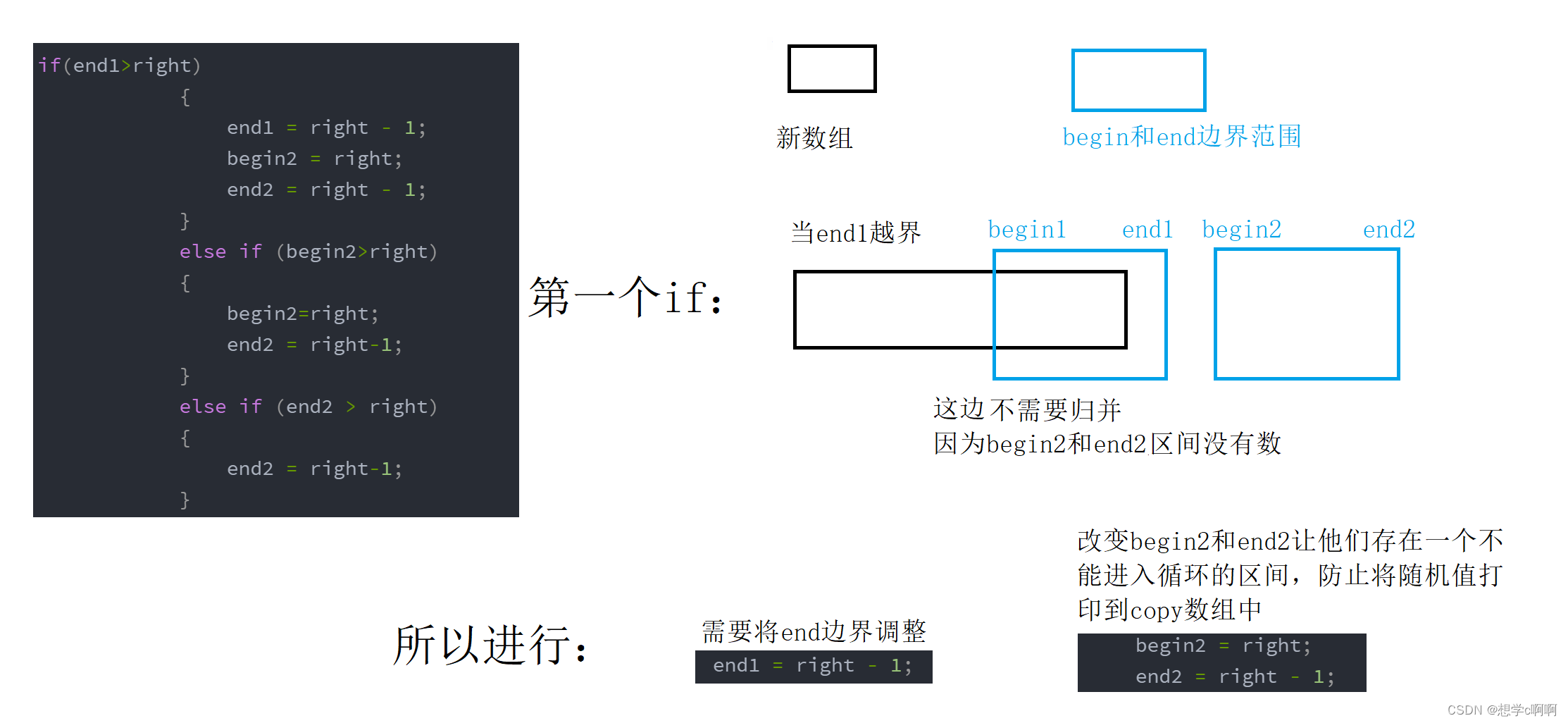

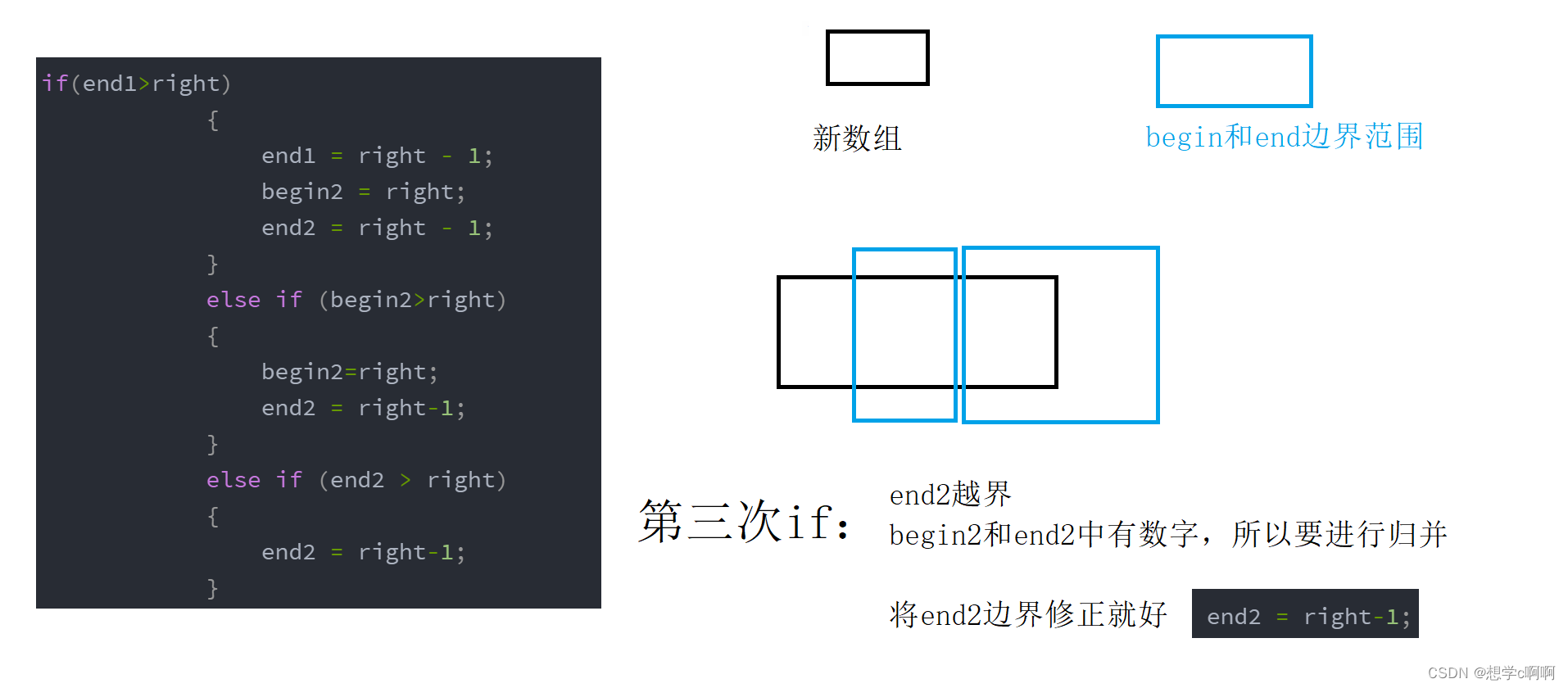
因为我们梭哈处理,所以不能进行break跳出循环
因为当我们break后,copy没有复制所有数
就会赋值给arr数组后有随机值产生
非梭哈
非梭哈就是归并哪部分的数字,就直接对arr进行复制
所以和梭哈的区别就是在边界调整时,可以进行break。
代码部分
void merge_sort_NO_all_in(int* arr, int arrsize)
{
int* copy = (int*)malloc(sizeof(int) * arrsize);
assert(copy);
int gap = 1;
while (gap < arrsize)
{
for (int i = 0; i < arrsize; i+=gap*2)
{
int begin1 = i, end1 = i + gap-1;
int begin2 = i + gap, end2 = gap * 2 + i - 1;
int g = i;
if (end1 > arrsize-1 || begin1 > arrsize-1)
{
//这里可以进行break
break;
}
if (end2 > arrsize)
{
end2 = arrsize - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] > arr[begin2])
{
copy[g++] = arr[begin2++];
}
else
{
copy[g++] = arr[begin1++];
}
}
while (begin1 <= end1)
{
copy[g++] = arr[begin1++];
}
while (begin2 <= end2)
{
copy[g++] = arr[begin2++];
}
//边归并边拷贝
for (int f = i; f <= end2; f++)
{
arr[f] = copy[f];
}
}
gap *= 2;
}
}
计数排序
这个计数排序是三大非比较排序之一。
在特定的部分很有特效
思路也很简单
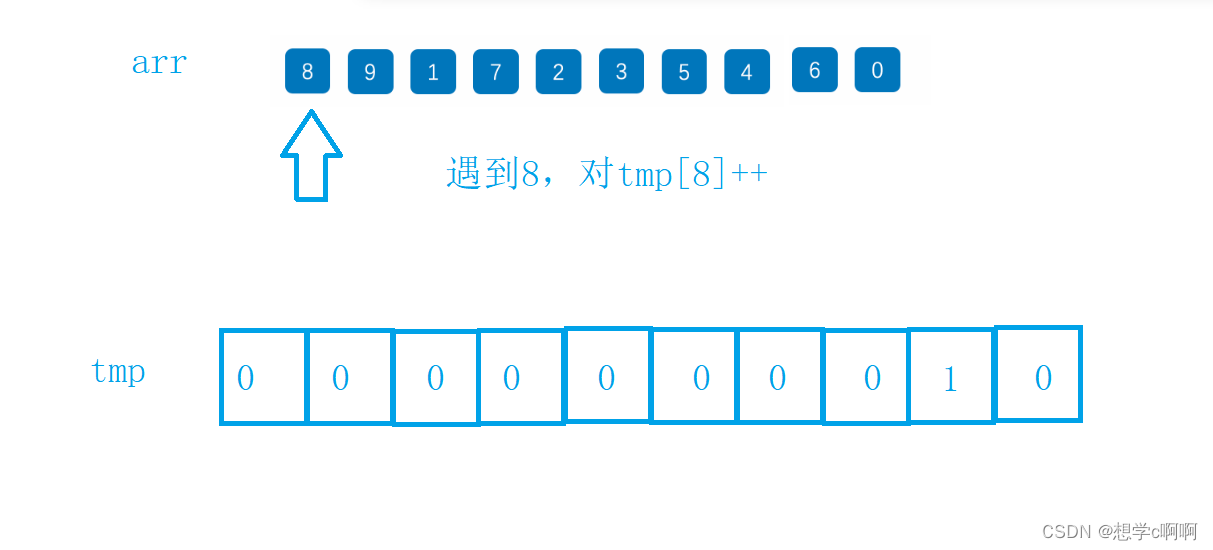
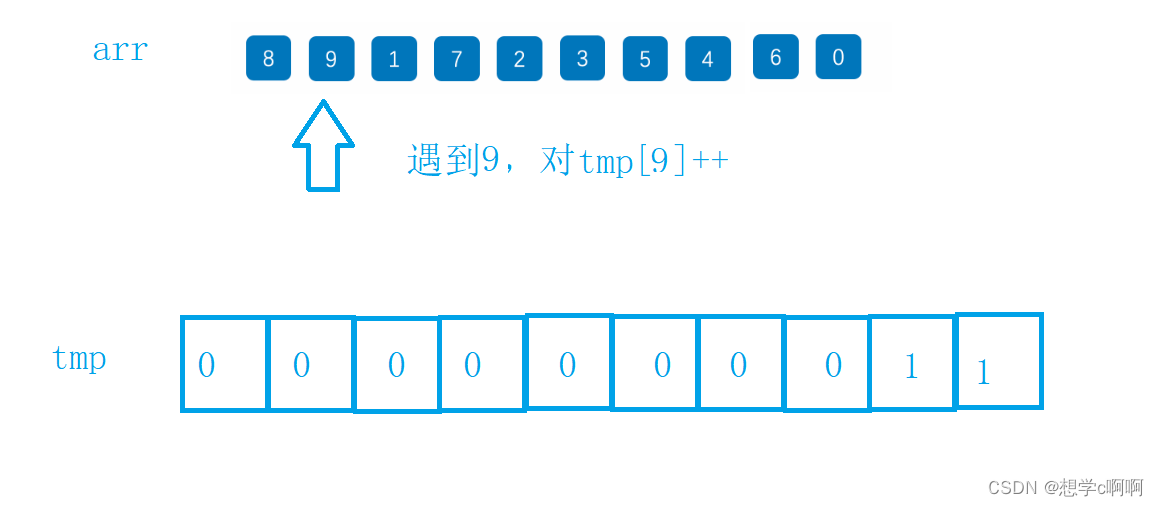
大致思路就是这样
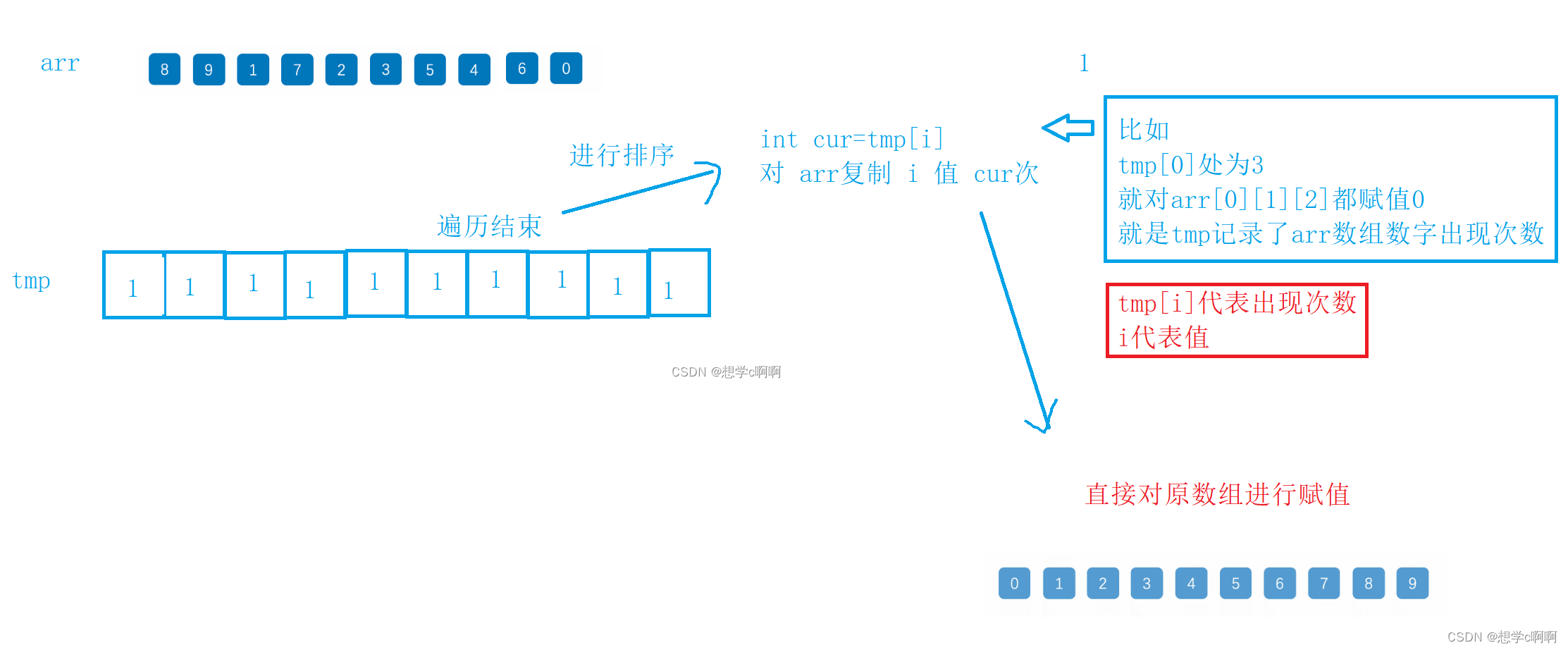
但是如果是最大值100,最小值是90的数组
这样的静态计数方法就不太好好用了
这里的代码是优化的动态计数排序法
代码部分
void countdata_sort(int* arr,int arrsize)
{
int max = arr[0];
int min = arr[0];
for (int i = 1; i < arrsize; i++)
{
if (max < arr[i])
{
max = arr[i];
}
if (min > arr[i])
{
min = arr[i];
}
}
//找到最大值最小值的范围进行数组开辟
int numsize = max - min+1;
int* ptr = (int*)malloc(sizeof(int) * numsize);
assert(ptr);
//将新数组所有数调成0
for (int i = 0; i < numsize; i++)
{
ptr[i] = 0;
}
//统计老数组的数字出现个数,在新数组++
for (int i = 0; i < arrsize; i++)
{
ptr[arr[i]-min]++;
}
int j = 0;
//将新数组的数按规定方式赋值给老数组
for (int i = 0; j < arrsize; i++)
{
while (ptr[i]--)
{
arr[j++] = i + min;
}
}
}
特性总结