PVA-MVSNet论文名为：Pyramid Multi-view Stereo Net with Self-adaptive View Aggregation，主要是用了一个自适应的聚合模块来在构建代价体时不用均匀的方差、而是让不同的特征体具有一定的选择注意力权重来对最终的代价体做贡献，同时对于多尺度的的深度图输出使用MVSNet的光度一致性约束、几何一致性约束来用小尺度上置信度高的深度代替大尺度上置信度低的深度。

---

本文是MVSNet系列的第7篇，建议看过【论文精读1】MVSNet系列论文详解-MVSNet之后再看便于理解。

一、问题引入

• 传统方法在处理匹配歧义、重建完整度上有缺陷
• MVSNet等基于学习的方法通过学习传统立体对应（stereo correspondences）所难以获取的深度特征信息来解决匹配模糊的问题，但输入的多视角图片往往都是做同样的处理和贡献，事实上不同视角图片由于光照、相机几何参数、场景内容可变性等不同，它们所采集到的图像特征也具有差异。
• 图像的多尺度的信息没有被充分的使用以改善三维重建的鲁棒性和完整性。

二、创新点

• 提出了自适应视图聚合（self-adaptive view aggregation），逐元素地聚合来自不同视图图像之间的残差，从而引导多个特征体聚合为一个归一化的代价体。
• 提出用多度量（multi-metric）来聚合多尺度（multi-scale）的金字塔图像信息，改善重建鲁棒性和完整性。

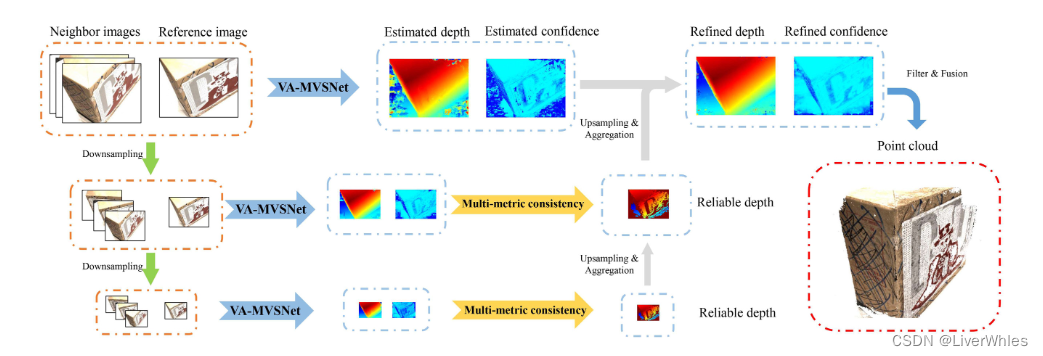
三、论文模型

遵循MVSNet的基本流程，区别在于
（1）特征提取部分使用2D UNet完成
（2）特征体聚合为代价体的步骤由直接方差替换为自适应试图聚合模块
（2）使用多尺度的图片金字塔生成不同尺度的深度图，并逐步利用不同度量（光度、几何一致性）用粗糙的深度图细化更精细的深度图

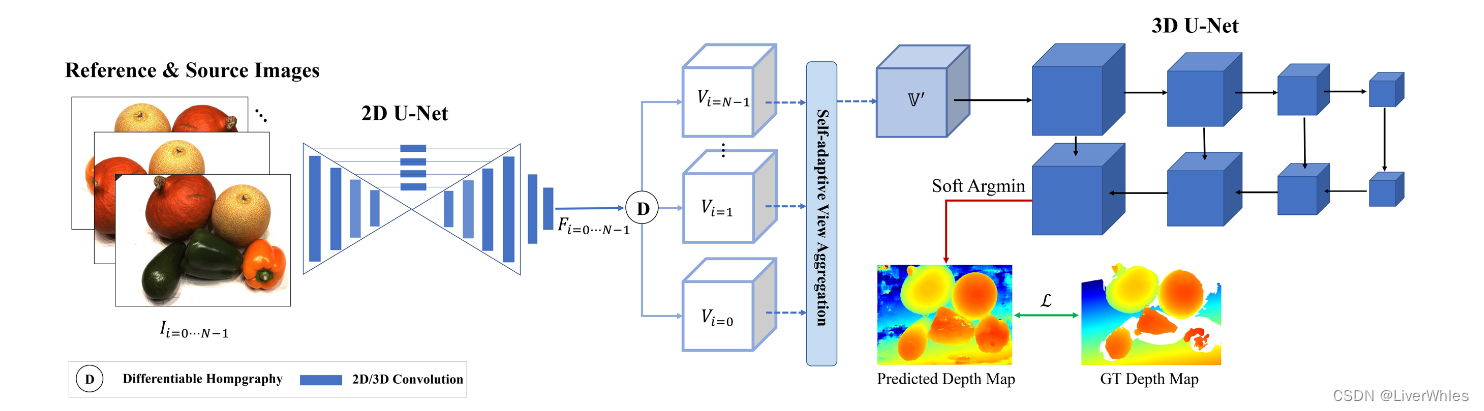
1.特征提取

利用2D Unet提取具有更大感受野的深度图像特征，特征图尺寸为[H/4, W/4, C(32)]

2.自适应试图聚合（Self-adaptive View Aggregation）

该部分包含两个聚合模块来实现自适应视图选择来聚合不同视图下的方差，分别是pixel-wise view aggregation和voxel-wise view aggregation

2.1 逐像素视图聚合（pixel-wise view aggregation）

该部分假设在深度方向上的权重一致，只在宽和高的维度上计算各像素的方差选择权重，利用权重注意力图来聚合得到代价体。

流程图示为：

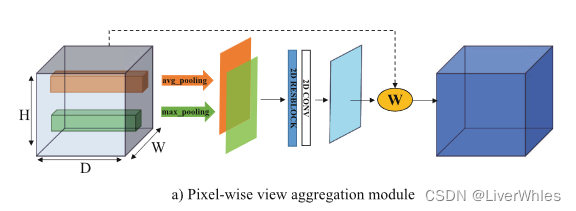
用公式表述整个过程为：
$$v_{i,d,h,w}^{{}^{\prime }}=v_{i,d,h,w}-v_{0,d,h,w}$$

图最左端的方块为残差的特征体，i为特征体的序号（即各特征图做微分变换后得到的的N个），d为深度，h,w为高和，这一步即对两个特征体上各通道各像素位置求残差

$$f_{h,w}=CONCAT(max\_pooling(\Vert v_{d,h,w}^{{}^{\prime }}{\Vert }_1),avg\_pooling(\Vert v_{d,h,w}^{{}^{\prime }}{\Vert }_1))$$
$$w_{h,w}=PA-Net(f_{h,w})$$

从残差代价体中沿深度方向pooling以求最大和平均并concat在一起作为训练特征，输入到一个2D的PA-Net（包含几个2D卷积层和ResNet块）当中进行训练，输出是一张以像素为单位的选择注意力权重图。

$$c_{d,h,w}=\frac{{\sum }_{i=1}^{N-1}(1+w_{h,w})\odot v_{i,d,h,w}^{{}^{\prime }}}{N-1}$$

w_h,w代表与宽、高尺寸一致的选择注意力权重图，令第i个特征体的差v’ 沿宽和高组成的各通道与该权重图逐元素点乘，并对各特征体差操作后的结果求均值，这样来实现不同视图特征体使用不同权重的效果

2.2 逐体素视图聚合（voxel-wise view aggregation）

该部分在深度方向上计算方差选择权重，与2.1思路一致，只不过是用3D卷积来计算出一个深度方向上的3D权重选择块，之后在深度方向上根绝权重计算出代价体。

流程图示为：

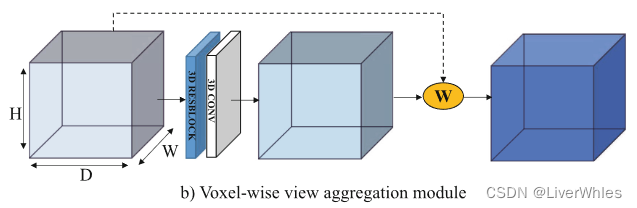
计算公式为：$$c_{d,h,w}=\frac{{\sum }_{i=1}^{N-1}(1+w_{d,h,w})\odot v_{i,d,h,w}^{{}^{\prime }}}{N-1}$$

3.深度图估计器（Depth Map Estimator）

该步骤与MVSNet完全一致了，用3D Unet正则化代价体得到概率体，然后沿深度方向求期望

论文指出由于自适应的视图聚合模块，在此处得到的深度图已经比MVSNet好了，示意图如下：

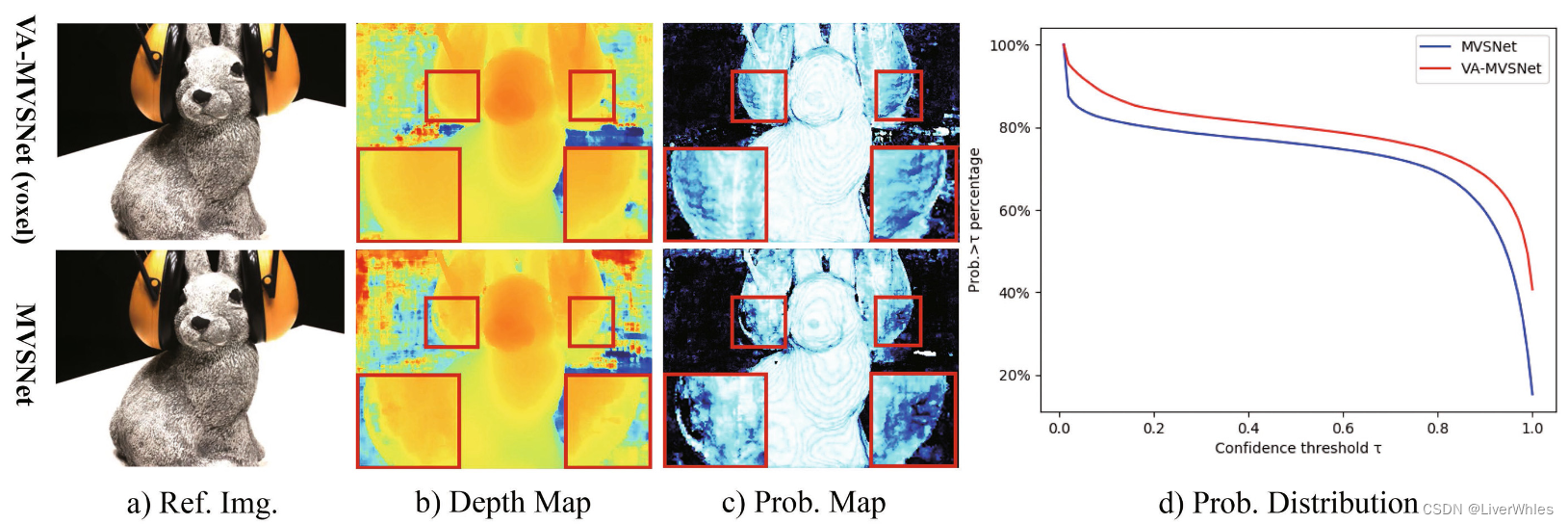
在红色方框中，上图为经过了VA（voxel）模块聚合后计算出的深度图，相比下图MVSNet对于深度近似、但由于反光而导致的深度不均匀现象被改善，而且从整体概率图、深度置信度分布上观察对于这些部分的深度都更确信。

4. 多度量金字塔深度聚合（Multi-metric Pyramid Depth Map Aggregation）

经过VA模块聚合的效果基础上，为了进一步重建的鲁棒性和完整性，提出了一种利用多度量（其实就是MVSNet里的光度和几何一致性）在不同尺度的深度图上进行聚合、优化深度推断的方法。

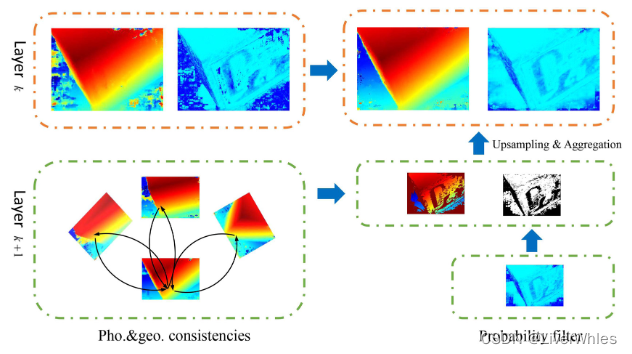
• 方法动机：
  对于第k层（大尺度）推断的深度图上可能存在一些由于匹配歧义而导致的低置信度、错误的深度，而在k+1层**（小尺度）上存在推断可能存在可靠的深度**
• 具体做法：
  利用光度一致性、几何一致性两个度量，筛选出小尺度上大于可信阈值上的点，通过上采样得到与大尺度图片上一致的尺寸，若大尺度对应位置的可信度小于阈值，则替换，从而实现金字塔自上而下（小->大）的深度聚合。

四、模型效果