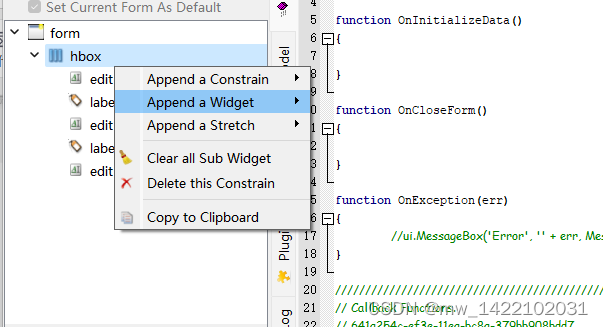
1. SM2国密算法介绍

SM2算法全称是SM2椭圆曲线公钥密码算法（SM是商用密码的拼音缩写），是一种基于“椭圆曲线”的密码ECC(Elliptic Curve Cryptography)。2016年，SM2成为中国国家密码标准。 在商用密码体系中，SM2主要用于替换RSA加密算法。

SM2为非对称加密，基于ECC。该算法已公开。由于该算法基于ECC，故其签名速度与秘钥生成速度都快于RSA。ECC 256位（SM2采用的就是ECC 256位的一种）安全强度比RSA 2048位高，但运算速度快于RSA。旧标准的加密排序C1C2C3 新标准 C1C3C2，C1为65字节第1字节为压缩标识，这里固定为0x04，后面64字节为xy分量各32字节。C3为32字节。C2长度与原文一致。

国密SM2算法也是基于椭圆曲线公钥算法，椭圆曲线上的运算都是和国际算法一样的，国密SM2规范中给出了推荐曲线，所以首先需要加载国密推荐参数。

国密 SM2 的算法基础是椭圆曲线，公式：

算法是基于数学的，SM2 定义曲线上的群运算加减乘，通过SM2公私钥的生成理解。

1. 首选一条椭圆曲线，即固定 a、b 的值，假设选择的是上图所示曲线。

2. 随机选择一个点 P 为基点，曲线做切线，经过 Q 点，切点 R1。

3. 基于 x 轴做 R1 的对称点 R，则 SM2 定义加法为 P + Q = R，这就是椭圆曲线加法。

4. 求 2 倍点，当 P = Q 时，即 P + P = R = 2P，则 R 是 P 的 2 倍点。

5. 求 3 倍点，3P = P + 2P = P + R，经过 P、R 做直线，交于椭圆曲线点 M1, 基于 x 轴对称点 M 则是 3 倍点，依次类推。

6. 求 d 倍点，假设我们同样次数为 d，运算倍点为 Q。

7. d 为私钥，Q 为公钥。所以私钥是一个大整数，公钥是一个点坐标。

上面的几何推理是为了方便理解，实际取值都是在质数有限域上。密码专家们经过推理和运算，已经为我们选择了质数有限域上的最优椭圆曲线，除非有特殊需要，否则不需要自定义曲线。

 

2. 数据格式

ASN.1数据类型定义表

Tag (decimal)	Tag (hex)	Type
2	02	INTEGER
3	03	BIT STRING
4	04	OCTET STRING
5	05	NULL
6	06	OBJECT IDENTIFIER
12	0C	UTF8String
16	10 (and 30)*	SEQUENCE and SEQUENCE OF
17	11 (and 31)*	SET and SET OF
19	13	PrintableString
22	16	IA5String
23	17	UTCTime
24	18	GeneralizedTime

2.1 密钥数据格式

2.1.1 私钥数据格式

SM2算法私钥数据格式的ASN.1定义为：

SM2PrivateKey ::= INTEGER

生成私钥：带“EC PARAMETERS”与不带“EC PARAMETERS”，只需要增加参数-noout。

openssl ecparam -genkey -name SM2 -out sm2.key  #带ec parameter
​
-----BEGIN EC PARAMETERS-----
BggqgRzPVQGCLQ==
-----END EC PARAMETERS-----
-----BEGIN EC PRIVATE KEY-----
MHcCAQEEINlSELboVsYit7SgBFlM5Zny24X9a7TnyUaK5cTVydPMoAoGCCqBHM9V
AYItoUQDQgAEw2I0OMqw39s0oin/S53J63C/GkFkWVR7H0b6063HqiInNVBEpfRF
AWysN5eJydvHtwDJ6G6g5UbNp9lMjDXfCQ==
-----END EC PRIVATE KEY-----
​
openssl ecparam -genkey -name SM2 -out sm2.key -noout  #不带ec parameter
​
-----BEGIN EC PRIVATE KEY-----
MHcCAQEEINlSELboVsYit7SgBFlM5Zny24X9a7TnyUaK5cTVydPMoAoGCCqBHM9V
AYItoUQDQgAEw2I0OMqw39s0oin/S53J63C/GkFkWVR7H0b6063HqiInNVBEpfRF
AWysN5eJydvHtwDJ6G6g5UbNp9lMjDXfCQ==
-----END EC PRIVATE KEY-----

openssl ecparam默认生成SM2私钥格式是PEM，可以选择输出格式为DER。

openssl ec -in sm2.key -outform DER -out sm2_pri.der

查看私钥密钥格式ASN.1内容

openssl asn1parse -in sm2.key
​
    0:d=0  hl=2 l= 119 cons: SEQUENCE          
    2:d=1  hl=2 l=   1 prim: INTEGER           :01
    5:d=1  hl=2 l=  32 prim: OCTET STRING      [HEX DUMP]:D95210B6E856C622B7B4A004594CE599F2DB85FD6BB4E7C9468AE5C4D5C9D3CC
   39:d=1  hl=2 l=  10 cons: cont [ 0 ]        
   41:d=2  hl=2 l=   8 prim: OBJECT            :sm2
   51:d=1  hl=2 l=  68 cons: cont [ 1 ]        
   53:d=2  hl=2 l=  66 prim: BIT STRING 
​
#ASN.1 Dump 私钥数据二进制文件
dumpasn1 sm2_pri.der
​
offset length
  0 119: SEQUENCE {
  2   1:   INTEGER 1
  5  32:   OCTET STRING
       :     D9 52 10 B6 E8 56 C6 22 B7 B4 A0 04 59 4C E5 99
       :     F2 DB 85 FD 6B B4 E7 C9 46 8A E5 C4 D5 C9 D3 CC
 39  10:   [0] {
 41   8:     OBJECT IDENTIFIER sm2ECC (1 2 156 10197 1 301)
       :     }
 51  68:   [1] {
 53  66:     BIT STRING
       :       04 C3 62 34 38 CA B0 DF DB 34 A2 29 FF 4B 9D C9
       :       EB 70 BF 1A 41 64 59 54 7B 1F 46 FA D3 AD C7 AA
       :       22 27 35 50 44 A5 F4 45 01 6C AC 37 97 89 C9 DB
       :       C7 B7 00 C9 E8 6E A0 E5 46 CD A7 D9 4C 8C 35 DF
       :       09
       :     }
       :   }
​
0 warnings, 0 errors.
​
#hexdump 私钥二进制文件
hexdump -v -e '/1 "%02x " ' -e '16/1 "" "\n"' sm2_pri.der
​
30 77 02 01 01 04 20 d9 52 10 b6 e8 56 c6 22 b7
b4 a0 04 59 4c e5 99 f2 db 85 fd 6b b4 e7 c9 46
8a e5 c4 d5 c9 d3 cc a0 0a 06 08 2a 81 1c cf 55
01 82 2d a1 44 03 42 00 04 c3 62 34 38 ca b0 df
db 34 a2 29 ff 4b 9d c9 eb 70 bf 1a 41 64 59 54
7b 1f 46 fa d3 ad c7 aa 22 27 35 50 44 a5 f4 45
01 6c ac 37 97 89 c9 db c7 b7 00 c9 e8 6e a0 e5
46 cd a7 d9 4c 8c 35 df 09 

2.1.2公钥数据格式

公钥有两大种表示，通常是压缩或未压缩

2.1.2.1 未压缩公钥

通常以前缀04开头，后跟两个256位数字；一个用于点的x坐标，另一个用于点的y坐标。前缀04用于区分未压缩的公共密钥和以02或03开头的压缩公共密钥

即04||x||y

2.1.2.2 压缩公钥

因为方程式的左侧是，所以y的解是平方根，它可以具有正值或负值。所得的y坐标可以在x轴之上或之下。因为该曲线是对称的，所以它在x轴上像镜子一样反射。因此，我们必须存储y的符号（正数或负数）；因为每个选项代表一个不同的点和一个不同的公钥。在素数为p的有限域上用二进制算术计算椭圆曲线时，y坐标为偶数或奇数，对应于前面所述的正/负号。所以为了区分y的两个可能值，如果y为偶数，则存储压缩的公钥，前缀为02，如果奇数为03，则允许软件从x坐标正确推断出y坐标，然后解压缩指向该点的完整坐标的公钥。

SM2算法公钥数据格式的ASN.1定义为：

SM2PublicKey ::= BIT STRING

SM2PublicKey为BIT STRING类型，内容为04‖X‖Y，其中，X和Y分别标识公钥的x分量和y分量，其长度各为256位。

生成公钥：

openssl ec -in sm2.key -pubout -outform PEM -out sm2_pub.key 

-----BEGIN PUBLIC KEY-----
MFkwEwYHKoZIzj0CAQYIKoEcz1UBgi0DQgAEw2I0OMqw39s0oin/S53J63C/GkFk
WVR7H0b6063HqiInNVBEpfRFAWysN5eJydvHtwDJ6G6g5UbNp9lMjDXfCQ==
-----END PUBLIC KEY-----

选择输出格式为DER

openssl ec -in sm2.key -pubout -outform DER -out sm2_pub.der

查看私钥密钥格式ASN.1内容

openssl asn1parse -in sm2_pub.key
​
    0:d=0  hl=2 l=  89 cons: SEQUENCE          
    2:d=1  hl=2 l=  19 cons: SEQUENCE          
    4:d=2  hl=2 l=   7 prim: OBJECT            :id-ecPublicKey
   13:d=2  hl=2 l=   8 prim: OBJECT            :sm2
   23:d=1  hl=2 l=  66 prim: BIT STRING  
​
#ASN.1 Dump 公钥数据二进制文件
dumpasn1 sm2_pub.der
​
offset length
  0  89: SEQUENCE {
  2  19:   SEQUENCE {
  4   7:     OBJECT IDENTIFIER ecPublicKey (1 2 840 10045 2 1)
 13   8:     OBJECT IDENTIFIER sm2ECC (1 2 156 10197 1 301)
       :     }
 23  66:   BIT STRING
       :     04 C3 62 34 38 CA B0 DF DB 34 A2 29 FF 4B 9D C9
       :     EB 70 BF 1A 41 64 59 54 7B 1F 46 FA D3 AD C7 AA
       :     22 27 35 50 44 A5 F4 45 01 6C AC 37 97 89 C9 DB
       :     C7 B7 00 C9 E8 6E A0 E5 46 CD A7 D9 4C 8C 35 DF
       :     09
       :   }
​
0 warnings, 0 errors.
​
#hexdump 公钥二进制文件
hexdump -v -e '/1 "%02x " ' -e '16/1 "" "\n"' sm2_pub.der
​
30 59 30 13 06 07 2a 86 48 ce 3d 02 01 06 08 2a
81 1c cf 55 01 82 2d 03 42 00 04 c3 62 34 38 ca
b0 df db 34 a2 29 ff 4b 9d c9 eb 70 bf 1a 41 64
59 54 7b 1f 46 fa d3 ad c7 aa 22 27 35 50 44 a5
f4 45 01 6c ac 37 97 89 c9 db c7 b7 00 c9 e8 6e
a0 e5 46 cd a7 d9 4c 8c 35 df 09

2.2 加密数据格式

SM2算法加密后的数据格式的ASN.1定义为：

SM2Cipher ::= SEQENCE {
XCoordinate	INTEGER,	-- x分量
YCoordinate	INTEGER,	-- y分量
HASH	OCTET STRING SIZE(32),	-- 杂凑值
CipherText	OCTET STRING	-- 密文
}

其中，HASH为使用SM3算法对明文数据运算得到的杂凑值，其长度固定为256位。CipherText是与明文等长的密文。

参考sm2_demo.c加解密样例代码。

编译sm2_demo.c

gcc sm2_demo.c -L /usr/lib -lssl -lcrypto -o sm2_demo

运行./sm2_demo 生成sm2_encrypt.bin文件。

./sm2_demo
SM2 private key (in hex form):
D95210B6E856C622B7B4A004594CE599F2DB85FD6BB4E7C9468AE5C4D5C9D3CC

x coordinate in SM2 public key (in hex form):
C3623438CAB0DFDB34A229FF4B9DC9EB70BF1A416459547B1F46FAD3ADC7AA22

y coordinate in SM2 public key (in hex form):
27355044A5F445016CAC379789C9DBC7B700C9E86EA0E546CDA7D94C8C35DF09

Message length: 16 bytes.
Message:
0x00  0x01  0x02  0x03  0x04  0x05  0x06  0x07  0x08  0x09  0x0a  0x0b  0x0c  0x0d  0x0e  0x0f  

Ciphertext length: 123 bytes.
Ciphertext (ASN.1 encode):
0x30  
0x79  0x02  0x20  0x15  0xd6  0x7f  0xc3  0x84  0x21  0x7a  0x28  0xd5  0x89  0xaf  0x3a  0x09  
0x32  0xf8  0xdf  0x03  0xd9  0xaa  0x3e  0x13  0x0b  0x46  0x17  0xe6  0x8d  0x0d  0x10  0xce  
0xe9  0xe7  0x08  0x02  0x21  0x00  0xc5  0x60  0x37  0xbe  0x2a  0x33  0x84  0xb5  0x06  0xdd  
0x48  0x6b  0x2c  0x3e  0xd2  0x2b  0xc1  0x81  0x6e  0x76  0x6b  0x7d  0x9d  0x69  0xcc  0x81  
0x57  0x31  0x52  0xd5  0x1f  0xb1  0x04  0x20  0x26  0xfd  0xa6  0x66  0xf5  0x87  0x77  0x67  
0x99  0x93  0x2a  0x5f  0x14  0x33  0x21  0x17  0xe9  0x0d  0x9d  0x1d  0xf3  0x81  0x8b  0x65  
0x70  0xc3  0x79  0xa9  0xb7  0xd1  0xc7  0x96  0x04  0x10  0x3b  0x63  0x89  0x5a  0x35  0x7c  
0x3d  0x4d  0x1f  0xad  0x73  0x0a  0xa1  0x89  0xc2  0x5f  

Decrypted plaintext length: 16 bytes.
Decrypted plaintext:
0x00  
0x01  0x02  0x03  0x04  0x05  0x06  0x07  0x08  0x09  0x0a  0x0b  0x0c  0x0d  0x0e  0x0f  

Encrypt and decrypt data succeeded!

查看加密数据格式ASN.1内容

#ASN.1 Dump 加密数据二进制文件
dumpasn1 sm2_encrypt.bin

offset length
  0 121: SEQUENCE {
  2  32:   INTEGER
       :     15 D6 7F C3 84 21 7A 28 D5 89 AF 3A 09 32 F8 DF
       :     03 D9 AA 3E 13 0B 46 17 E6 8D 0D 10 CE E9 E7 08
 36  33:   INTEGER
       :     00 C5 60 37 BE 2A 33 84 B5 06 DD 48 6B 2C 3E D2
       :     2B C1 81 6E 76 6B 7D 9D 69 CC 81 57 31 52 D5 1F
       :     B1
 71  32:   OCTET STRING
       :     26 FD A6 66 F5 87 77 67 99 93 2A 5F 14 33 21 17
       :     E9 0D 9D 1D F3 81 8B 65 70 C3 79 A9 B7 D1 C7 96
105  16:   OCTET STRING 3B 63 89 5A 35 7C 3D 4D 1F AD 73 0A A1 89 C2 5F
       :   }

0 warnings, 0 errors.

#hexdump 数字签名二进制文件
hexdump -v -e '/1 "%02x " ' -e '16/1 "" "\n"' sm2_encrypt.bin 

30 79 02 20 15 d6 7f c3 84 21 7a 28 d5 89 af 3a
09 32 f8 df 03 d9 aa 3e 13 0b 46 17 e6 8d 0d 10
ce e9 e7 08 02 21 00 c5 60 37 be 2a 33 84 b5 06
dd 48 6b 2c 3e d2 2b c1 81 6e 76 6b 7d 9d 69 cc
81 57 31 52 d5 1f b1 04 20 26 fd a6 66 f5 87 77
67 99 93 2a 5f 14 33 21 17 e9 0d 9d 1d f3 81 8b
65 70 c3 79 a9 b7 d1 c7 96 04 10 3b 63 89 5a 35
7c 3d 4d 1f ad 73 0a a1 89 c2 5f 

2.3 签名数据格式

SM2 签名一般有两种数据格式，国标(GM/T 0009-2012 SM2 密码算法使用规范)规定签名数据格式，使用ASN.1 格式定义，具体格式如下： 通常使用硬件加密机加签产生的数字数字签名将会使用这种格式。SM2 数字签名另外一种方式就比较简单，格式为R|S，即直接将两者拼接在一起表示。

SM2算法签名数据格式的ASN.1定义为：

SM2Signature ::= SEQUENCE{
R	INTEGER,	-- 签名值的第一部分
S	INTEGER	-- 签名值的第二部分
}

R和S的长度各为256位。

对SM2公钥SM3杂凑值进行数字签名：

openssl sm3 sm2_pub.der
SM3(sm2_pub.der)= a760be75c573ac4c0a2350da375b52265ebb2623774c58a446c1b8751c8fbcf8

#生成SM2公钥SM3杂凑值二进制文件
openssl dgst -sm3 -binary sm2_pub.der > sm3_pub.bin

hexdump -v -e '/1 "%02x " ' -e '16/1 "" "\n"' sm3_pub.bin 

a7 60 be 75 c5 73 ac 4c 0a 23 50 da 37 5b 52 26
5e bb 26 23 77 4c 58 a4 46 c1 b8 75 1c 8f bc f8

#生成数字签名二进制文件
openssl dgst -sign sm2.key -out sm2_pk_sm3.sign sm3_pub.bin

#ASN.1 Dump 数字签名二进制文件
dumpasn1 sm2_pk_sm3.sign 

offset length
  0  68: SEQUENCE {
  2  32:   INTEGER
       :     21 80 5A 21 15 C7 68 31 06 80 6D 7B E7 44 F3 BD
       :     1A EF 23 04 97 81 6D 3C 2C FD 90 83 BE AC 9F 0B
 36  32:   INTEGER
       :     1A DC 37 70 B6 5D 31 7B 2C 65 8B 81 96 6A 2E F8
       :     C6 A5 FD A7 BA DA 7F 0D 69 42 6E D3 A7 1C CA E2
       :   }
0 warnings, 0 errors.

#hexdump 数字签名二进制文件
hexdump -v -e '/1 "%02x " ' -e '16/1 "" "\n"' sm2_pk_sm3.sign

30 44 02 20 21 80 5a 21 15 c7 68 31 06 80 6d 7b
e7 44 f3 bd 1a ef 23 04 97 81 6d 3c 2c fd 90 83
be ac 9f 0b 02 20 1a dc 37 70 b6 5d 31 7b 2c 65
8b 81 96 6a 2e f8 c6 a5 fd a7 ba da 7f 0d 69 42
6e d3 a7 1c ca e2

3. SM2数字签名与验签算法流程

3.1 数字签名算法符号定义:

A,B：使用公钥密码系统的两个用户。

dA：用户A的私钥。

E(Fq)： Fq上椭圆曲线E 的所有有理点(包括无穷远点O)组成的集合。

e：密码杂凑函数作用于消息M的输出值。

e′：密码杂凑函数作用于消息M ′的输出值。

Fq：包含q个元素的有限域。

G：椭圆曲线的一个基点，其阶为素数。

Hv()：消息摘要长度为v比特的密码杂凑函数。

IDA：用户A的可辨别标识。

M：待签名的消息。

M′：待验证消息。

modn：模n运算。例如， 23mod7=2。

n：基点G的阶(n是#E(Fq)的素因子)。

O：椭圆曲线上的一个特殊点，称为无穷远点或零点，是椭圆曲线加法群的单位元。

PA：用户A的公钥。

q：有限域Fq中元素的数目。

a,b： Fq中的元素，它们定义Fq上的一条椭圆曲线E。

x ∥ y： x与y的拼接，其中x、 y可以是比特串或字节串。

ZA：关于用户A的可辨别标识、部分椭圆曲线系统参数和用户A公钥的杂凑值。

(r,s)：发送的签名。

(r′,s′)：收到的签名。

[k]P：椭圆曲线上点P的k倍点，即， [k]P= P + P + · · · + P（k个P， k是正整数）。

[x,y]：大于或等于x且小于或等于y的整数的集合。

数字签名算法由一个签名者对数据产生数字签名,并由一个验证者验证签名的可靠性。每个签名者有一个公钥和一个私钥,其中私钥用于产生签名,验证者用签名者的公钥验证签名。在签名的生成程之前,要用密码杂凑算法对 M(包含和待签消息 M)进行压缩;在验证过程之前,要用密码杂凑算法对 M'(包含和待验证消息 M')进行压缩。作为签名者的用户 A 具有长度为entlenA比特的可辨别标识IDA,记ENTLA 是由整数entlenA 转换而成的两个字节,在本部分规定的椭圆曲线数字签名算法中,签名者和验证者都需要用密码杂凑算法求得用户 A 的杂凑值。按 GB/T32918.1—2016中4.2.6和4.2.5给出的方法,将椭圆曲线方程参数a、b、G 的坐标、和的坐标、,  的数据类型转换为比特串。

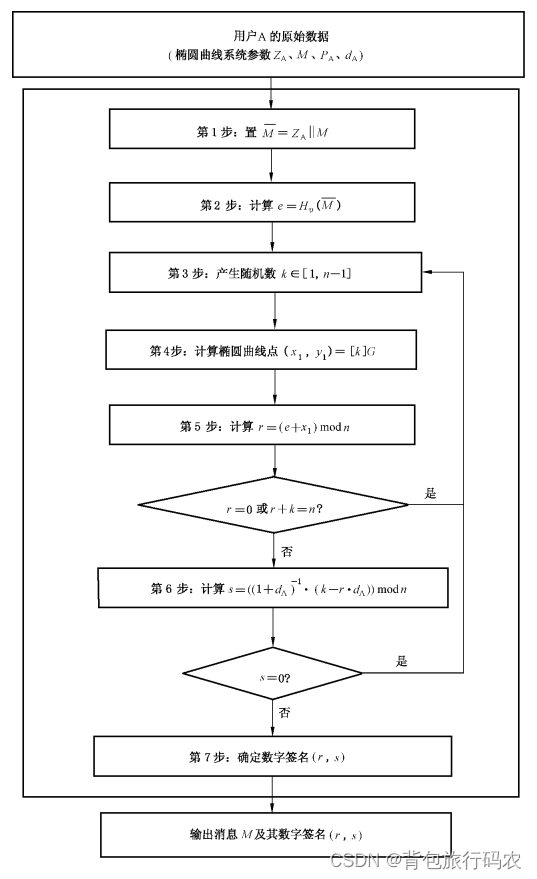
3.2 数字签名的生成算法及流程

3.2.1 数字签名的生成算法

设待签名的消息为 M,为了获取消息 M 的数字签名(r,s),作为签名者的用户 A 应实现以下运算步骤:

 3.2.2 数字签名生成算法流程

              

 

3.3 数字签名的验证算法及流程

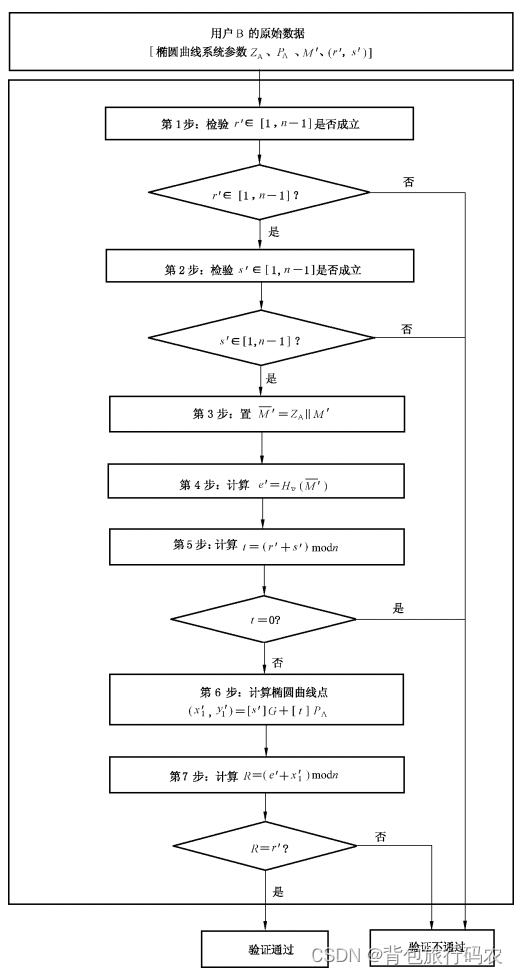
3.3.1 数字签名的验证算法

为了检验收到的消息 M' 及其数字签名(r',s'),作为验证者的用户 B应实现以下运算步骤:

 

  3.3.2 数字签名验证算法流程

                 

 

参考文献

SM2国密算法/椭圆曲线密码学ECC之数学原理 - 简书 (jianshu.com)

Elliptic Curve Cryptography: a gentle introduction - Andrea Corbellini

GMT 0003.5-2012 SM2椭圆曲线公钥密码算法推荐曲线参数

GMT 0003.2-2012 SM2椭圆曲线公钥密码算法第2部分：数字签名算法