2021 第十二届蓝桥杯大赛软件赛决赛, 国赛，C/C++ 大学B组题解

news2024/11/16 5:40:55

2021 第十二届蓝桥杯大赛软件赛决赛, 国赛，C/C++ 大学B组题解

文章目录

      • 第1题 —— 带宽 （5分）
      • 第2题 —— 纯质数 （5分）
      • 第3题 —— 完全日期 （10分）
      • 第4题 —— 最小权值 （10分）
      • 第5题 —— 大写 （15分）
      • 第6题 —— 123 （15分）
      • 第7题 —— 异或变换 （20分）
      • 第8题 —— 二进制问题 （20分）
      • 第9题 —— 翻转括号序列 （25分）
      • 第10题 —— 异或三角 （25分）

补题链接：地址

在这里插入图片描述
这把的线段树题不太好做，两个二进制dp题（虽然都可以dfs转移）都有点麻烦。
如果前面的粗心大意，找规律/结论公式没找到，或者前缀和二分和二叉树没写出来的话，就寄了。

第1题 —— 带宽 （5分）

在这里插入图片描述

  • 题目：Mbps和MB的单位换算，不会有人不会吧，不会吧不会吧。
  • 答案：25
#include<bits/stdc++.h>
using namespace std;

int main(){
    cout<<200/8;
    return 0;
}

第2题 —— 纯质数 （5分）

在这里插入图片描述

  • 题意：纯质数是本身为质数，而且每一位的数字也是质数的数。求1-20210605有多少个这样的数。
  • 思路：直接暴力枚举每个数，拆出来判断是不是即可。
  • 答案：1903
//T2
#include<bits/stdc++.h>
using namespace std;
int isprime(int x){
	if(x==1)return 0;
	for(int i = 2; i*i <= x; i++){
		if(x%i==0){
			return 0;
		}
	}
	return 1;
}
set<int>se;
int check(int x){
	int t = x;
	while(t){
		int r = t%10;
		if(!se.count(r))return 0;
		t = t/10;
	}
	return 1;
}
int main(){
	se.insert(2);
	se.insert(3);
	se.insert(5);
	se.insert(7);
	int cnt = 0;
	for(int i = 1; i <= 20210605; i++){
		if(isprime(i)){
			if(check(i)){
				cnt++;
			}
		}
	}
	cout<<cnt<<"\n";
	return 0;
}

第3题 —— 完全日期 （10分）

在这里插入图片描述

  • 题意：定义完全日期表示，一个日期的年月日的各位数字之和是完全平方数。求给定起止的两个日期间有多少个完全日期。
  • 思路：暴力枚举日期，然后判断一下是不是即可。
  • 答案：977
//T3
#include<bits/stdc++.h>
using namespace std;
int days[13] = {0,31,28,31,30,31,30,31,31,30,31,30,31};
int main(){
	int cnt = 0;
	for(int y = 2001; y <= 2021; y++){
		if((y%100!=0&&y%4==0)||y%400==0){
			days[2] = 29;
		}else{
			days[2] = 28;
		}
		for(int m = 1; m <= 12; m++){
			for(int d = 1; d <= days[m]; d++){
				int s = 0;
				int yy=y, mm=m,dd=d;
				while(yy){s+=yy%10; yy/=10;}
				while(mm){s+=mm%10; mm/=10;}
				while(dd){s+=dd%10; dd/=10;}
				int q = (int)sqrt(s);
				if(q*q==s){
					cnt++;
				}
			}
		}
	}
	cout<<cnt<<"\n";
	return 0;
}

第4题 —— 最小权值 （10分）

在这里插入图片描述

  • 题意：给出一颗二叉树，定义他的权值规则，求最小可能的权值是多少。
  • 答案：2653631372
  • 思路：dp状态为i个节点的最小权值，转移的时候枚举左子树有多少个节点，右子树的节点数就知道了，然后也知道比当前节点数小的最小权值，直接扫一遍取min可以了。
//dp[i]: 有i个节点的树的最小权值
#include<bits/stdc++.h>
using namespace std;
int main(){
    vector<long long> dp(2022, LLONG_MAX);
    dp[0] = 0;
    for (int i = 1; i <= 2021; i++) {
        for (int j = 0; j < i; j++) {
            dp[i] = min(dp[i], 1+2*dp[j]+ 3*dp[i-j-1] + j*j*(i-j-1));
        }
    }
    cout << dp[2021] << endl;
    return 0;
}

第5题 —— 大写 （15分）

在这里插入图片描述

  • 题意：字母大小写转换
  • 思路：直接输出即可
//T5
#include<bits/stdc++.h>
using namespace std;
int main(){
	string s;  cin>>s;
	for(int i = 0; i < s.size(); i++)
		if(islower(s[i]))s[i] = toupper(s[i]);
	cout<<s;
	return 0;
}

第6题 —— 123 （15分）

在这里插入图片描述
在这里插入图片描述

  • 题意：给一个有规律的数列，112123123412345这样排列下去。T组询问，每次求区间的和。
  • 思路：前缀和+暴力可以过70%。
//baoli 70%
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 1e6+10;

LL num[maxn], ss[maxn];

LL sum(LL x){
	LL xx = x;
	while(xx>0){
		LL t = (LL)sqrt(xx*2);
		if(t*(t+1)==xx*2){
			break;
		}
		xx--;
	}
	
	LL t = sqrt(xx*2);
	LL ans = (1+x-xx)*(x-xx)/2;
	
	ans += ss[t];
	return ans;
}


int main(){
	for(int i = 1; i < maxn; i++){
		num[i] = num[i-1]+1;
		ss[i] = ss[i-1]+(1+i)*i/2;
	}
	
	int T;  cin>>T;
	while(T--){
		LL l, r;  cin>>l>>r;
		cout<<sum(r)-sum(l-1)<<"\n";
	}
	return 0;
}
  • 其实再优化一下，预处理出前缀和，然后加个二分去搜索就可以过（参考了一下官方题解，补题懒得重新敲啦）
//二分，100%
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e7;

int cnt = 2, tot = 2;
int sum[N + 100], mid[N + 100], b[N + 100];
void init(){
    sum[1] = 1;  mid[1] = 1;  b[1] = 1;
    for (int i = 3; i <= 1e12; i += cnt) {
        sum[tot] =  sum[tot - 1] + cnt;//sum数组存的是 1 2 3 4 5 6这个等差数列的前缀和
        mid[tot] = mid[tot - 1] + sum[tot];//mid数组存的是 1 12 123 1234 12345这个数组的前缀和
        b[tot++] = i;//b数组存的是 1 12 123 1234 12345这个数组的每一组最后一位数的下标
        cnt++;
    }
}

signed main() {
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    init();
    int T;  cin >> T;
    while (T--) {
        int l, r;  cin >> l >> r;
        int idxl = lower_bound(b + 1, b + tot + 1, l) - b  ;//二分
        int idxr = lower_bound(b + 1, b + tot + 1, r) - b  ;
        cout << mid[idxr - 1] + sum[idxr - (b[idxr] - r)] - mid[idxl - 1] - sum[idxl - (b[idxl ] - l + 1)] << '\n';
    }
    return 0;
}
  • 或者发现这题有个结论公式，直接丢上去就可以过
//结论，100%
#include<bits/stdc++.h>
using namespace std;
long long sum(long long u){
    double uh = sqrt(2*u)-0.5;
    long long n = (long long)uh;
    u = u-(n*(n+1))/2;
    return (u*(u+1))/2+(n*(n+1)*(n+2))/6;
}
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int T;  cin>>T;
    while(T--){
        long long l, r;  cin>>l>>r;
        cout<<sum(r)-sum(l-1)<<"\n";
    }
    return 0;
}

第7题 —— 异或变换 （20分）

在这里插入图片描述
在这里插入图片描述

  • 题意：给出一个长为n的01串，求经过t次变换后的串是什么。每次变换让si=si-1异或上si。
  • 思路：暴力打表找规律发现，变换2的x次方次的串会变回原来的串，所以可以减掉这个次数，剩下的暴力变换即可。
//T7
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
string c[1000005];
int main(){
	LL n, t;  cin>>n>>t;
	string a;  cin>>a;
    LL tt = 1;  
    while (tt < n) tt *= 2;  
    t %= tt;
	for(int k = 1; k <= tt; k++){
		string b = a;
		for(int i = 1; i < n; i++){
			b[i] = (a[i-1]-'0')^(a[i]-'0')+'0';
		}
		a = b;
		// cout<<k<<": "<<b<<"\n";
		c[k] = b;
	}
	cout<<c[t]<<"\n";
	return 0;
}

第8题 —— 二进制问题 （20分）

在这里插入图片描述

  • 题意：求1-n的二进制中有多少个数恰好有K个1，n<1e18
  • 思路：1e18那么必然不能枚举，所以肯定是结论题，或者跟K有关。直接结论发现有点难，那么从K的角度来考虑，二进制相关的dp。
  • 考虑所有比n小的数的二进制规律：如果n的某一位为1
    （1）这一位为0的二进制数，剩下所有低位任意取，可能结果一个组合数C(n,k) ，已经为1的位数不变。
    （2）这一位为1的二进制数，递归到下一位，但已经为1的位数加1。
    然后dfs处理。
//AC，100%
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL num, k;  
vector<LL>vc;

//计算组合数C(n,k)
LL f[70][70];
LL cal(LL n, LL k){
    if(f[n][k])return f[n][k];
    if(n==k || k==0)return 1;
    if(n<k)return 0;
    return f[n][k]=cal(n-1,k-1)+cal(n-1,k);
}

//solve
LL dfs(int i, int cnt){
    if(cnt==k)return 1;
    if(i<0 || cnt>k)return 0;
    LL res = 0;
    if(vc[i]){
        res += cal(i, k-cnt);
        res += dfs(i-1, cnt+1);
    }else{
        res += dfs(i-1, cnt);
    }
    return res;
}

int main(){
    cin>>num>>k;
    while(num){
        vc.push_back(num%2);  num /= 2;
    }
    cout<<dfs(vc.size()-1, 0);
	return 0;
}
  • 写不来的话可以交个枚举的暴力，有50%
//50%
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int main(){
	LL n, k;  cin>>n>>k;
	int cnt = 0;
	for(LL i = 1; i <= n; i++){
		LL x = i, t = 0;
		while(x){ t+=x&1; x>>=1;}
		if(t==k)cnt++;
	}
	cout<<cnt<<"\n";
	return 0;
}

第9题 —— 翻转括号序列 （25分）

在这里插入图片描述

在这里插入图片描述

  • 题意：长为n的括号序列，操作m次，每次可以将l-r区间的括号都变位相反，或者求L为左端点，最长的合法括号序列对应的R。

  • 考虑操作2：
    合法括号序列可以被等价地描述为，序列中左括号与右括号数量相等，且序列的任意前缀中，左括号数量不小于右括号数量。
    更易接受的叙述是：如果将左括号赋值为 1，右括号赋值为 −1，则序列的和与最小前缀和均为 0。

  • 考虑操作1：
    将每个数都减去自己的2倍，1-2=-1，（-1）-（-2）=1，即可实现取反的效果。

  • 然后建立线段树，并在每个结点维护：
    和、最小前缀和、所有最小前缀和对应端点中最靠右者。

  • 查询时，在线段树上二分，如果最小前缀和已经小于 0 ，则考虑向左走；否则继续向右走。由于 l 与二分所得端点（r’）所构成区间最小前缀和恰好为 0 ，答案即为 [l,r ′ ] 所有最小前缀和对应端点中最靠右者。

  • 补题不想敲代码啦，贴一个dalao的能过的代码把。参考

//AC
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pii pair<int,int>
#define pb push_back
#define mp make_pair
#define vi vector<int>
#define vll vector<ll>
#define fi first
#define se second
#define mid ((l + r) >> 1)
#define ls (t << 1)
#define rs (t << 1 | 1)
const int maxn = 1e6 + 5;
const int mod = 1e9 + 7;
struct Node{int mx , mi , sw , add;}tr[maxn << 2];
int a[maxn];
char s[maxn];
int n , m;
template <typename T>
void read(T & x){ x = 0;T f = 1;char ch = getchar();while(!isdigit(ch)){if(ch == '-') f = -1;
ch = getchar();}while (isdigit(ch)){x = x * 10 + (ch ^ 48);ch = getchar();}x *= f;}
template <typename T>
void write(T x){if(x < 0){putchar('-');x = -x;}if (x > 9)write(x / 10);putchar(x % 10 + '0');}

void pushup (int t){
    tr[t].mx = max(tr[ls].mx , tr[rs].mx);
    tr[t].mi = min(tr[ls].mi , tr[rs].mi);
}
void build (int t , int l , int r){
    if (l == r){
        tr[t].mx = tr[t].mi = a[l];
        return ;
    }
    build(ls , l , mid);
    build(rs , mid + 1 , r);
    pushup(t);
}
void D_sw (int t){
    int mx = tr[t].mx , mi = tr[t].mi;
    tr[t].mx = -mi; tr[t].mi = -mx;
    tr[t].sw ^= 1;
    tr[t].add *= -1;
}
void D_add (int t , int c){
    tr[t].mi += c;
    tr[t].mx += c;
    tr[t].add += c;
}
void pushdown (int t){
    if (tr[t].sw){
        D_sw(ls);
        D_sw(rs);
        tr[t].sw = 0;
    }
    if (tr[t].add){
        D_add(ls,tr[t].add);
        D_add(rs,tr[t].add);
        tr[t].add = 0;
    }
}
void Swap (int t , int l , int r , int L , int R){
    if (L <= l && r <= R){
        D_sw(t);
        return ;
    }
    pushdown(t);
    if (L <= mid) Swap(ls , l , mid , L , R);
    if (R > mid) Swap(rs , mid + 1 , r , L , R);
    pushup(t);
    return ;
}
void add (int t , int l , int r , int L , int R , int c){
    if (L <= l && r <= R){
        D_add(t , c);
        return ;
    }
    pushdown(t);
    if (L <= mid) add(ls , l , mid , L , R , c);
    if (R > mid) add(rs , mid + 1 , r , L , R , c);
    pushup(t);
    return ;
}
// 单点查值
int ask1 (int t , int l , int r , int p){
    if (l == r) return tr[t].mx;
    pushdown(t);
    if (p <= mid) return ask1(ls , l , mid , p);
    return ask1(rs , mid + 1 , r , p);
}
// 找[p,n]中离p最近的一个小于c的点
int ask2 (int t , int l , int r , int p , int c){
    // -1 代表该区域没有 < c 的数
    if (l == r) return l;
    pushdown(t);
    // 优先往左走,再考虑什么情况下可以往左走
    // PS:这么走，答案只是"可能"存在
    int res = -1;
    if (tr[ls].mi < c && p <= mid)
        res = ask2(ls , l , mid , p , c);
    if (res != -1) return res;
    // 程序能执行到这里代表左边不存在答案了.只能往右走了
    if (tr[rs].mi < c)
        res = ask2(rs , mid + 1 , r , p , c);
    return res;
}
// 找[1,p]中离p最近的小于c的点
int ask3 (int t , int l , int r , int p , int c){
    if (l == r) return l;
    pushdown(t);
    int res = -1;
    if (tr[rs].mi < c && p > mid)
        res = ask3(rs , mid + 1 , r , p , c);
    if (res != -1) return res;
    if (tr[ls].mi < c) res = ask3(ls , l , mid , p , c);
    return res;
}
int pre[maxn];
void modify (int x){
    if (x == 0) return ;
    int v = ask1(1 , 1 , n , x);
    Swap(1 , 1 , n , 1 , x);
    if (x != n) add(1 , 1 , n , x + 1 , n , -2 * v);
}
int main()
{
    read(n); read(m);
    scanf("%s" , s + 1);
    for (int i = 1 ; i <= n ; i++){
        if (s[i] == '(') a[i] = a[i - 1] + 1;
        else a[i] = a[i - 1] - 1;
    }
    build(1 , 1 , n);
    for (int i = 1 ; i <= m ; i++){
        int op , x , y; read(op);
        if (op == 1){
            read(x);read(y);
            modify(x - 1);
            modify(y);
        }else {
            read(x);
            int v;
            if (x == 1) v = 0;
            else v = ask1(1 , 1 , n , x - 1);
            int p = ask2(1 , 1 , n , x , v);
            if (p == -1) p = n + 1;
            int r = ask3(1 , 1 , n , p - 1 , v + 1);
            if (r == -1) r = 0;
            printf("%d\n" ,  (r <= x ? 0 : r));
        }
    }
    return 0;
}

第10题 —— 异或三角 （25分）

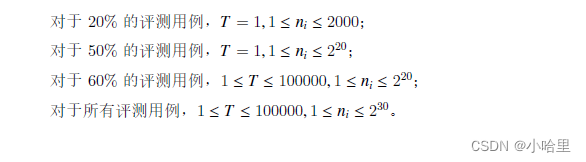
在这里插入图片描述
在这里插入图片描述

  • 题意：给出T个数，对每个数x求出有多少个三元组abc满足都小于x，且abc异或和为0，且abc能构成三角形。
  • 异或和为0，意味三个数的每一位上1的个数只能为0或2。
  • 设n>a>b>c，那么对每一位来说，abc的该位分别为110的状态要先于101出现。
  • 考虑能组成三角形，即a<b+c，而异或为0得到a=b^c，所以b^c<b+c，所以必定存在着一组011的状态。
  • 枚举ac，保证满足以上的限制条件后输出即可，参考
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL n, f[40][2][2][2][2];
LL dfs(LL a, LL c, LL i, LL j, LL k){
    if(i==-1)return k;
    if(f[i][j][k][c][a] != -1)return f[i][j][k][c][a];
    LL top = j ? ((n>>i)&1) : 1 ;
    LL res = 0;
    for(LL bt = 0; bt <= top; bt++){
        LL nj = (j&&(bt==top));
        if(bt){
            if(!a)res += dfs(1,c,i-1,nj,k); //a最大，最高位1给a和b 
            else{
                res += dfs(1,c,i-1,nj,k); //给a、b 
				res += dfs(1,1,i-1,nj,k); //给a、c 
            }
        }else{
            res += dfs(a,c,i-1,nj,k);        //全0 
			if(c!=0) res+=dfs(a,1,i-1,nj,1); //给b、c，若c==0，给b、c的话会使b>a  
        }
    }
    return f[i][j][k][c][a]=res;
}
int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int T;  cin>>T;
    while(T--){
        cin>>n;
        memset(f,-1,sizeof f);
        cout<<dfs(0,0,31,1,0)*6LL<<"\n";
    }
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/518352.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MySQL之快速查询的秘籍 【B+树索引】

MySQL之快速查询的秘籍 【B+树索引】

前言 本文章收录在MySQL性能优化原理实战专栏&#xff0c;点击此处查看更多优质内容。 本文摘录自 ▪ 小孩子4919《MySQL是怎样运行的&#xff1a;从根儿上理解MySQL》 &#x1f604;学完前面我们讲解了InnoDB数据页的7个组成部分&#xff0c;知道了各个数据页可以组成一个双…
阅读更多...
Linux 多线程（3）多线程应用、信号量、线程池、单例模式

Linux 多线程（3）多线程应用、信号量、线程池、单例模式

应用 生产者与消费者模型 生产者与消费者模型---设计模式的一种 设计模式--程序员针对一些典型的应用场景所给出的一种典型的解决方案 应用场景--在有大量数据任务产生的同时需要进行任务处理的场景 如果采用单执行流解决&#xff1a; 效率低下 资源利用不一定合理&#xff08;…
阅读更多...
【Python数据分析】常用内置函数（一）

【Python数据分析】常用内置函数（一）

&#x1f64b;‍ 哈喽大家好&#xff0c;本次是python数据分析、挖掘与可视化专栏第四期 ⭐本期内容&#xff1a;常用内置函数 &#x1f3c6;系列专栏&#xff1a;Python数据分析、挖掘与可视化 &#x1f44d;“总有一段时光悄悄过去然后永远怀念.” 文章目录 前言类型转换int(…
阅读更多...
Vue---列表渲染

Vue---列表渲染

目录 一、列表渲染的基本使用 &#xff08;1&#xff09;渲染数组数据 &#xff08;2&#xff09;渲染对象数据 二、v-for指令的高级用法 三、列表过滤 四、列表排序 一、列表渲染的基本使用 使用v-for指令可以将数组&#xff0c;对象数据渲染成列表视图 &#xff08;1&a…
阅读更多...
前端自学好还是培训好？女生有多适合学前端，我来告诉你！

前端自学好还是培训好？女生有多适合学前端，我来告诉你！

2023年了&#xff0c;你是否还在迷茫或者每个月拿着5/6k做着卷死的工作&#xff0c;不但存不下钱还不能好好享受生活&#xff0c;如果是&#xff0c;那你真该考虑一下转行了。 好程序员先说说前端到底怎么开始学&#xff1a; 有的伙伴说今年28岁了&#xff0c;学的会计&#xf…
阅读更多...
Vue中的MVVM【第三篇】

Vue中的MVVM【第三篇】

大纲&#xff1a; MVVM图示 &#x1f308; 一、MVVM简介 简单来说&#xff1a;MVVM&#xff08;M-VM-M&#xff09;&#xff0c;一种更好的UI模式解决方案&#xff0c;MVVM通过数据双向绑定让数据自动地双向同步。 M(Model)&#xff1a;Model数据模型&#xff0c;json格式数据…
阅读更多...
Revit中如何创建曲面嵌板及一键成板

Revit中如何创建曲面嵌板及一键成板

一、Revit中如何创建曲面嵌板 在我们的绘图过程中可能会遇见一些曲面形状&#xff0c;而我们的常规嵌板没办法满足我们绘制的要求&#xff0c;我们今天学习如何在revit中绘制曲面嵌板。 1.新建“自适应公制常规模型”族&#xff0c;创建4个点图元并为其使用自适应。 2.在相同的…
阅读更多...
linux系统内核调试手段——动态输出

linux系统内核调试手段——动态输出

https://xuesong.blog.csdn.net/article/details/109522945?spm1001.2014.3001.5502 使用动态输出是系统内核调试的重要手段之一。 内核使用大量的pr_debug()/dev_dbg()函数来输出信息&#xff0c;使用了动态输出的技术。在使用动态输出时&#xff0c;记住需要挂载debugfs文件…
阅读更多...
Java 8 ConcurrentHashMap 源码分析

Java 8 ConcurrentHashMap 源码分析

文章目录 1. ConcurrentHashMap 的底层结构2. ConcurrentHashMap 的元素存储过程3. ConcurrentHashMap 的扩容3.1 扩容的过程3.2 源码分析 1. ConcurrentHashMap 的底层结构 JDK 1.8 的 ConcurrentHashMap 底层数据结构与 HashMap 基本相同&#xff0c;二者在容量机制、Entry …
阅读更多...
测试的分类（按测试对象、是否查看代码、开发阶段、实施组织...... + 思维导图总结）

测试的分类（按测试对象、是否查看代码、开发阶段、实施组织...... + 思维导图总结）

目录 一、测试的分类 1. 按测试对象划分 2. 按照是否查看代码划分 3. 按照开发阶段划分 4. 按照测试实施组织划分 5. 按照是否运行划分 6. 按照是否手工划分 7. 按照地域划分 二、总结 一、测试的分类 1. 按测试对象划分 &#xff08;1&#xff09;界面测试 简称UI测…
阅读更多...
Centos配置OpenVPN+OpenLDAP认证

Centos配置OpenVPN+OpenLDAP认证

Centos配置OpenVPNOpenLDAP认证 一、安装openvpn-auth-ldap插件二、配置ldap.conf文件三、配置openvpn中的server.conf文件四、配置客户端client.ovpn文件五、开启路由转发功能六、脚本编辑七、测试 Centos搭建OpenVPN的环境有很多资料&#xff0c;自行查询配置 一、安装openv…
阅读更多...
工作两年了，不想做客服，转行学数据分析改变未来！

工作两年了，不想做客服，转行学数据分析改变未来！

不想做客服&#xff0c;转行学数据分析改变未来&#xff01; 从今年开年以来&#xff0c;已经接触了很多转行人群的课程咨询&#xff0c;其中比较有代表性的原职业就是客服&#xff0c;听到对职业的抱怨大多是&#xff1a;工作辛苦&#xff0c;待遇又低&#xff0c;又没前途&am…
阅读更多...
基于WiFi的CSI数据做呼吸频率检测-python版

基于WiFi的CSI数据做呼吸频率检测-python版

一、概述 本Demo无需机器学习模型&#xff0c;Demo功能涉及的理论主要参考了硕士学位论文《基于WiFi的人体行为感知技术研究》&#xff0c;作者是南京邮电大学的朱XX&#xff0c;本人用python复现了论文中呼吸频率检测的功能。Demo实现呼吸速率检测的主要过程为&#xff1a; …
阅读更多...
15-721 chapter12 查询计划

15-721 chapter12 查询计划

查询模型 查询模型就是定义如何支持服务端多个并发服务&#xff0c;这里我们引入了worker的抽象概念&#xff0c;可以是线程也可以是进程&#xff0c;就是支持客户端请求并且返回结果的。 进程模型 进程池模型 不利于cache,并且进程之间的通信依赖于tcp&#xff0c;shared me…
阅读更多...
外贸独立站必备神器AB斗篷

外贸独立站必备神器AB斗篷

做独立站仿品的都知道&#xff0c;如果需要在FB、Google等平台上打广告&#xff0c;必须先上正品才能通过审核&#xff0c;而且就算通过了审核&#xff0c;后期平台也会不定期地去检查。所以当平台的审核爬虫来&#xff0c;商家必须先跳到正品网页规避审核&#xff0c;当买家过…
阅读更多...
FE_Vue学习笔记 - 模板语法[插值 指令] 数据绑定[v-bind v-model] 数据代理 事件

FE_Vue学习笔记 - 模板语法[插值 指令] 数据绑定[v-bind v-model] 数据代理 事件

尝试 Vue.js 最简单的方法是使用 Hello World 例子&#xff0c;你可以在浏览器新标签页中打开它&#xff0c;跟着例子学习一些基础用法&#xff0c;或者你也可以创建一个 .html 文件&#xff0c;然后通过如下方式引入 Vue&#xff1a; <!-- 开发环境版本&#xff0c;包含了…
阅读更多...
Java-Redis缓存穿透，击穿，雪崩和布隆算法

Java-Redis缓存穿透，击穿，雪崩和布隆算法

Java-Redis缓存穿透&#xff0c;击穿&#xff0c;雪崩和布隆算法 1.缓存穿透概念:2.如何解决缓存穿透:3.什么是缓存击穿?4.什么是缓存雪崩?5.导致缓存雪崩的原因:6.缓存穿透&#xff0c;缓存击穿&#xff0c;缓存雪崩的区别: 1.缓存穿透概念: 当一个用户想要查询数据时&…
阅读更多...
一文解析Menu Governor

一文解析Menu Governor

在现代操作系统中&#xff0c;往往很多时候并不需要去执行cpu密集型的任务&#xff0c;而每当这个时候&#xff0c;如果去持续的执行循环去等待新的任务发过来&#xff0c;那需要消耗巨大的能量。所以设计人员设计出一种空闲状态以此CPU进入低功耗模式。在Linux系统中&#xff…
阅读更多...
智能运维的集中告警平台实战思路 —— 紧耦合还是宽融合？

智能运维的集中告警平台实战思路 —— 紧耦合还是宽融合？

作者&#xff1a;擎创科技产品总监 Daniel 本文是节选&#xff0c;如感兴趣可留言一起探讨。 &#xff08; 我们在确定一个产品的思路和方向时&#xff0c;经常面临截然不同的选择。如同此文探讨的集中告警平台是否应跟集中监控平台紧绑定或松融合&#xff0c;具体的实战案例…
阅读更多...
[译] Dart 3 发布了

[译] Dart 3 发布了

[译] Dart 3 发布了 原文 https://medium.com/dartlang/announcing-dart-3-53f065a10635 https://ducafecat.com/blog/dart-3 来自 Google I/O 2023 的问候。今天&#xff0c;我们在 Mountain View 现场宣布 Dart 3——迄今为止最大的 Dart 发布&#xff01;Dart 3 包含三个主要…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023