导读

独立成分分析(ICA)是一种有效且普遍使用的EEG信号处理工具。为了减少计算时间，许多分析管道在ICA之前降低了EEG维数。Artoni及其同事(2018)的研究中就详细地描述了这种降维ICA(rdICA)对独立成分的偶极性和可靠性的有害影响。虽然ICA对于那些直接分析独立成分感兴趣的研究人员很有价值，但它更常用于清洗EEG数据。因此，需要直接检查通过rdICA去除伪影对EEG数据质量的影响。本研究对43名健康被试在执行主动听觉oddball任务的128导电极记录进行了注册分析。在以下条件下对每个被试的数据进行了预处理：①无降维的ICA；②仅包含64导电极的ICA；③ICA之前的PCA保留了原始数据99%的方差；④ICA之前的PCA保留了90%的方差。然后，通过测量平均振幅、单个试次平均振幅的标准测量误差(SME)以及N1和P3成分的分半信度来量化ERP数据质量。接下来，在一个独立的验证数据集中验证本研究结果。结果发现，在90%条件下，早期感觉成分的平均振幅在统计上和实际上都有显著的变化。出乎意料的是，SME仅在64导电极条件下更大。而且，rdICA对分半信度的影响在数据集之间是不一致的。基于此，本研究认为谨慎使用基于PCA的rdICA是有必要的。

前言

独立成分分析(ICA)是一种广泛应用且高效的电生理记录清洗工具。在EEG背景下，ICA的一个实际和理论限制是EEG中包含的独立成分(ICs)的数量等于用于记录的通道数量，而通道数量可能等于也可能不等于潜在信号源的真实数量。因此，通常会在ICA之前降低高密度EEG数据的维数。Artoni等人(2018)详细介绍了这种降维对所得独立成分(ICs)的偶极性和可靠性的有害影响。尽管该报告对直接分析大脑ICs的研究人员很有价值，但许多EEG研究人员在量化感兴趣的神经反应之前，主要使用ICA分离和去除少量非神经伪影成分。因此，有必要直接检查降维ICA(rdICA)伪影去除对EEG数据质量的影响。

为了解决这一差距，研究者考察了rdICA对主动听觉oddball任务中引发的N1和P3 ERP成分的影响。Oddball任务由一系列混合的罕见目标刺激和频繁的非目标刺激组成。对于主动oddball任务，参与者被要求做出行为反应以区分目标和非目标刺激；然而，即使在没有行为反应的情况下，也可以观察到与oddball分类相关的神经反应。听觉N1或N100成分在100ms左右有一个负峰，在额中央电极部位最大，被认为反映了早期感觉加工。它对新异的事物敏感度较弱，但对特定刺激的物理特征(包括音高和持续时间)高度敏感，同时受到选择性注意和唤醒水平的调节。后期的听觉P300具有广泛的正时程，峰值在250到500ms之间，并通过新异的声音增强。与N1成分不同，P300对刺激的物理特性不太敏感，因此被认为反映了更高水平的刺激分类过程。先前的研究估计，标准刺激和目标刺激的N1平均振幅的内部一致性(由Cronbach's α测量)分别为0.94和0.86，目标刺激的P3平均振幅为0.83。

本研究选择N1和P300作为感兴趣的主要成分。同样，选择在一个主动oddball任务情景中检查这些成分，因为它是一个基础和流行的ERP范式。此外，目前尚不清楚rdICA对早期感觉成分和晚期认知成分的影响是否存在差异。为了测试本研究的发现是否适用于其他EEG系统，任务范式和ERP成分，研究者对独立数据集进行了验证分析，其中描述了rdICA对使用不同EEG记录系统记录的DSCPT任务期间引发的视觉P1和N2成分的影响。

本研究侧重于两种降维技术：主成分分析(PCA)和电极分组，后者近似于收集低密度EEG数据(例如，64或32通道蒙太奇)。其他降维技术如因子分析和机器学习方法也存在，但这些在ICA之前并不常用，因此在本研究中没有进行考察。与ICA类似，PCA在许多领域无处不在；然而，ICA提取的是最大独立成分，PCA识别的是观测数据方差最大的正交向量序列，这些向量最大限度地解释观测数据中的方差。与ICA类似，PCA将返回与数据维数一样多的成分数量；但是，通常会设置一个阈值，将超过该阈值的主成分排除。确定此阈值的方法很多，但为了简单起见并与Artoni等人的研究保持一致，本研究专注于百分比方差阈值方法，其中每个PC所占的方差百分比按顺序相加(从占方差最大的PC开始)，直到达到阈值(例如，90%)。达到此阈值后，所有未包含在总和中的PC都将被排除。

也许EEG降维最简单的方法是向ICA提交一个较小的电极子集。本文研究这种方法是因为它比PCA计算效率更高：索引数组的时间复杂度为O(1)，而创建协方差/相关矩阵然后提取正交特征向量的时间复杂度为O(min(p^3，n^3))，其中p是变量的数量，n是个案数或观察数。在ICA之前对电极进行分组不仅在计算和概念上比PCA介导的rdICA更简洁，而且可能是评估更高密度电极蒙太奇是否会导致更好的基于ICA伪影去除的有用技术。鉴于EEG和ERP社区中关于收集高密度记录的成本(例如，更长的记录准备时间，桥接电极的可能性增加)是否大于假定收益(例如，更高的信噪比，更好的插值精度，更好的空间分辨率)存在相当大的争论，描述ICA伪影去除的质量如何受到电极密度的影响可能是有价值的。

为了量化rdICA的影响，本研究检查了被试水平的平均振幅、标准测量误差和分半信度。平均振幅经常用于量化成分的大小，因为它是一种无偏点估计，对非时间锁定噪声和不平衡试次设计具有鲁棒性。因此，本研究预计被试水平的平均振幅测量不会受到rdICA可能增加的非时间锁定噪声的影响。然而，即使rdICA对平均振幅没有显著影响，但它也可能导致ERP中单个试次噪声的不同水平。为了明确评估给定时间窗平均振幅下的单试次水平噪声，本研究使用了最近提出的标准测量误差(SME)。时间窗平均振幅的SME是通过取每个试次的平均振幅，计算这些单个试次平均振幅的标准差，然后除以试次数目的平方根来计算的。因此，如果单个试次平均振幅测量中有较大的噪声(即较大的标准差)，则SME将较大，表明单个试次平均振幅的精度较低。最后，许多ERP研究试图考察大脑电位与个体差异的关系，这需要可靠的ERP测量。正如Luck等人(2020)所讨论的，经典信度对给定样本的异质性程度很敏感，因此即使测量精度(例如SME)保持不变，较大的异质性也可能会导致更高的可靠性估计。因此，本研究评估了rdICA是否对ERP成分振幅的分半信度产生有意义的影响。

鉴于平均振幅对单个试次水平噪声的鲁棒性，本研究假定在ICA之前通过通道分组或PCA降低128通道EEG数据的维数，与全维ICA相比，被试水平的平均振幅差异可以忽略不计。此外，假设rdICA(通过PCA，而不是通道子集)与fdICA相比，在ERP振幅的可靠性方面的变化可以忽略不计，这将为在个体差异研究中使用降维方法提供证据。通过检验这些假设，本研究希望为从高维ERP数据中去除非神经伪影的最佳实践提供指导，并证明通过正确地使用降维技术可以避免全维ICA过高的计算成本。

方法

参与者

对43名参与者进行初步分析和对29名健康对照参与者进行验证分析。健康对照组的排除标准包括：智力障碍(智商＜70)、过去6个月有药物或酒精依赖、当前或既往中枢神经系统疾病、癫痫、电休克治疗史、颅骨骨折或意识丧失超过30min的头部损伤史、18岁以下或60岁以上、精神病病史、当前或既往抑郁或躁狂发作史，或抑郁、躁狂或精神障碍家族史。

主动听觉oddball任务

感兴趣的主要任务是一个主动听觉定向oddball任务，在运行Windows XP的戴尔电脑上使用Presentation软件呈现该任务。音调呈现时间为100ms，上升/下降时间为10ms，试次间隔为1200-1500ms。参与者在四个blocks中总共完成了800个试次。在第一个block中，参与者关注左耳，并在听到左耳高音时用右键单击鼠标。这种高目标音的音高为2400Hz，出现频率较低(占所有试次的10%)。注意耳中的低音频率为1600Hz，并且出现频率较高(占所有试次的40%)。在非注意耳中，出现不频繁的音调(1200Hz；占所有试次的10%)和频繁的音调(800Hz；占所有试次的40%)。在第二个block中，刺激呈现是相同的，但参与者被要求关注右耳。对于第三个和第四个block，音调水平是相反的(例如，前两个block呈现给右耳的音调，在第三和第四block中呈现给左耳)。

EEG采集和处理

使用BioSemi ActiveTwo系统收集用于初步分析的EEG数据，该系统带有差分放大器和高密度128电极蒙太奇和10个辅助电极：两个水平眼电图电极放置在双眼外眼角附近，两个垂直眼电图电极放置在右眼上方和下方，两个心电图电极放置在左右臂上，两个耳电极放置在左右耳垂上，两个肌电图电极放置在拇指下方的左右外展拇短肌上。在采集过程中，使用共模感应(CMS)和右腿驱动(DRL)接地电极以1024Hz采样无参考EEG。

预处理在EEGLAB v2021.1中进行。数据参考采用平均耳垂信号作为参考，使用二阶巴特沃斯以0.1Hz进行高通滤波，然后重采样至250Hz。使用具有默认值(频率范围=20-40Hz，epoch长度=0.5s，上限阈=10dB，epoch重叠=0.25s)的eeglab pop_rejcont函数自动拒绝噪声时段。使用带有以下默认参数的pop_clean_rawdata自动检测和删除坏电极：FlatlineCriterion=5，Channel Criterion=0.8，Line Noise Criterion=4。

然后将连续EEG数据进行四种平行ICA分解：①无降维的ICA；②仅包含奇数编号的ICA(BioSemi电极编号为A1-32，B1-32，C1-32和D1-32，共128个电极；这里只包括奇数编号的电极，例如A1，A3，A5，A7，...D31，它们提供了头皮的全覆盖，并接近64电极蒙太奇)；③ICA之前的PCA保留了原始数据99%的方差；④ICA之前的PCA保留了90%的方差。ICA通过pop_runica函数执行，使用默认的infomax算法，并启用了推荐的“扩展”选项。使用内置函数中基于协方差矩阵的正交旋转PCA。使用IClabel插件与默认参数自动识别眼部、肌肉、心脏通道噪声和线噪声伪影。分类为眼部、肌肉、心脏、通道噪声或线噪声的伪影(置信度为80%或更高)被自动拒绝。在ICA之后，被去除的通道通过球面样条方法进行插值。使用从-150到0ms的均值对平均ERPs进行基线校正。如果可用的不频繁试次少于25个(共160个)，则将该被试排除在外。N1成分先验定义于额中央部位(F1，FZ，F2，FC1，FCz，FC2和Cz)，P3定义于顶枕部位(P1，Pz，P2，PO3，PO4和POz)。N1平均振幅提取的先验时间窗为50-150ms，P3成分为250-500ms。目视检查了总平均波形，以确定这些先验时间窗是否覆盖了样本中的N1和P3成分范围，同时避免本研究的结果偏向特定的被试内效应。

统计分析

在初步分析中，使用6个因变量来衡量rdICA对ERP数据质量的影响：感觉N1平均振幅(频繁和罕见条件下的均值)，频繁-罕见P3平均振幅，感觉N1和频繁-罕见P3平均振幅的标准测量误差(SME)，以及感觉N1和频繁-罕见P3平均振幅的分半信度。对于平均振幅和SME测量，计算三个单尾相关样本t检验以进行比较：①全维ICA(fdICA) vs.64导电极ICA；②fdICA vs.ICA前PCA 99%的方差；③fdICA vs.ICA前PCA 90%的方差。为了控制1类错误率，初始alpha为0.05，邦弗罗尼校正为0.017(0.05/3=0.017)。给定alpha和样本量，统计检验能够以80%的概率(即power=0.8)检测到中等Cohen's d效应量为0.48或更大。

除了这些频率检验之外，本研究还计算了贝叶斯因子来比较零假设和备择假设的证据强度。零假设的先验分布是一个具有N-1个自由度的t分布，备择假设是柯西分布(即具有1个自由度的t分布)。这种方法是由Rouder等人(2009)推荐的，并且是本研究用于计算贝叶斯因子的BayesFactor R包的默认值。

成分的分半信度计算为参与者偶数试次和奇数试次均值之间的皮尔逊相关性。然后，使用Spearman-Brown公式对该信度系数进行校正，以解释试次数目分半的原因：

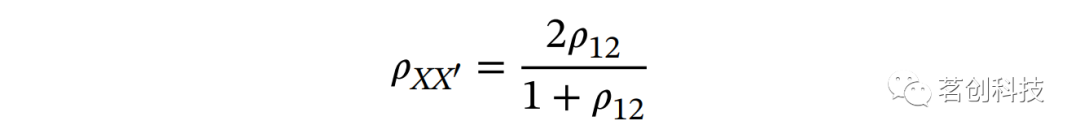
其中

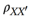
是Spearman-Brown校正的信度系数，ρ12是原始的分半信度系数。然后通过Fisher's Z变换将标准化：

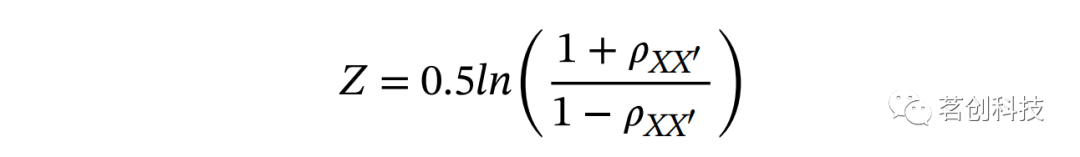
并计算出alpha为0.05/3的95%置信区间：

因此，对于每个预处理条件，估计相应95%置信区间的单个信度系数。

最后，为了确定rdICA是否可能导致更多混合ICs，从而导致ERP数据质量下降，本研究计算了未能自动分类为眼动、大脑、EKG、肌肉、通道噪声和线噪声的ICs所解释的方差百分比，每个参与者在每个预处理条件下的置信度为80%。然后，使用上述相同的被试内t检验方法来检验条件之间的显著差异。如果在混合ICs的数量和ERP成分中噪声的数量的预处理条件之间存在显著差异，则运行中介分析(中介R包)来测试混合ICs的增加是否解释了rdICA与数据质量下降之间的关系。

验证数据集

为了检验研究结果的普遍性，对29名健康对照的独立数据集进行相同的分析，这些健康对照被试完成了DS-CPT任务，并在BrainVision 128电极ActiCHamp系统上记录EEG数据。DSCPT呈现一系列从0到9的数字(刺激持续时间=29ms和SOA=1000ms)，并要求被试在目标数字“0”出现时按下按钮。检查双侧视觉P1和目标诱发N2的平均振幅，以及SME和分半信度的变化。所有条件下的PO7/PO8/P7/P8电极位置的P1时间窗为80-130ms。视觉N2是通过在电极Cz、FCz和Fz上取平均值的目标-非目标差异波测量的，时间窗为320-400ms，以获得有关数据集和范式的更多细节。

结果

平均振幅。基于对总平均波形的目视检查，将N1的时间窗从50-150ms调整为50-180ms，而P1、N2和P3的时间窗没有调整(N1和P3成分的波形和地形图见图1；P1和N2的相应图详见补充材料)。图2描述了在四种目标条件下，预处理后N1和P3平均振幅的变化程度。对于N1成分，没有观察到full vs. half、full vs. 99%比较的平均振幅的显著变化。然而，在90%方差阈值条件下，确实存在平均振幅的显著增加。假设N1是一个负成分，这种振幅的增加反映了N1的平均振幅接近于零。本研究观察到full vs. 90%比较的最大贝叶斯因子，这表明数据强烈支持备择假设(即，预处理条件之间的平均振幅存在差异)。对于本研究进行的三种条件比较中，P3差异波都没有显著差异。在各成分中，六个贝叶斯因子中有四个低于0.33，这表明数据更支持这四个比较的零假设(即，这些预处理条件之间没有显著差异)。有趣的是，P3振幅的full vs. half比较的贝叶斯因子大于3，表明数据更符合备择假设；然而，平均振幅的变化并没有达到预期的方向。换句话说，P3振幅在降维条件下较大，这可能表明信噪比增加，因为P3差异波是一个正向成分。

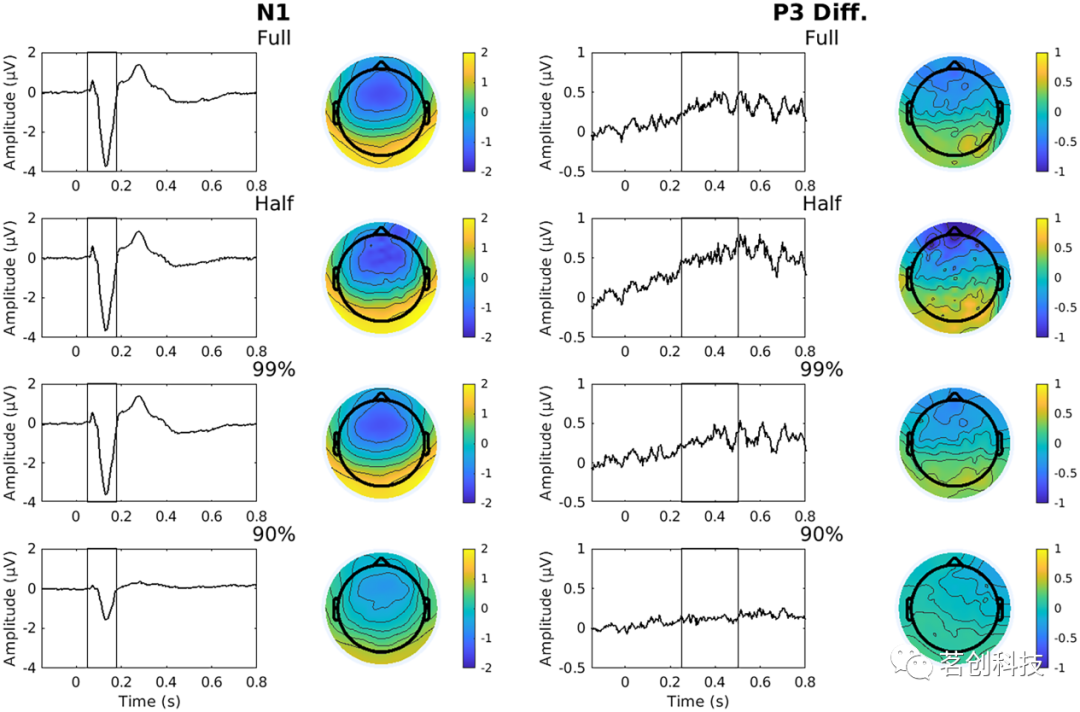
图1.按条件划分的总平均波形和地形图。N1成分是所有试次的平均值，而这里的P3是罕见试次减去频繁试次的差异波。

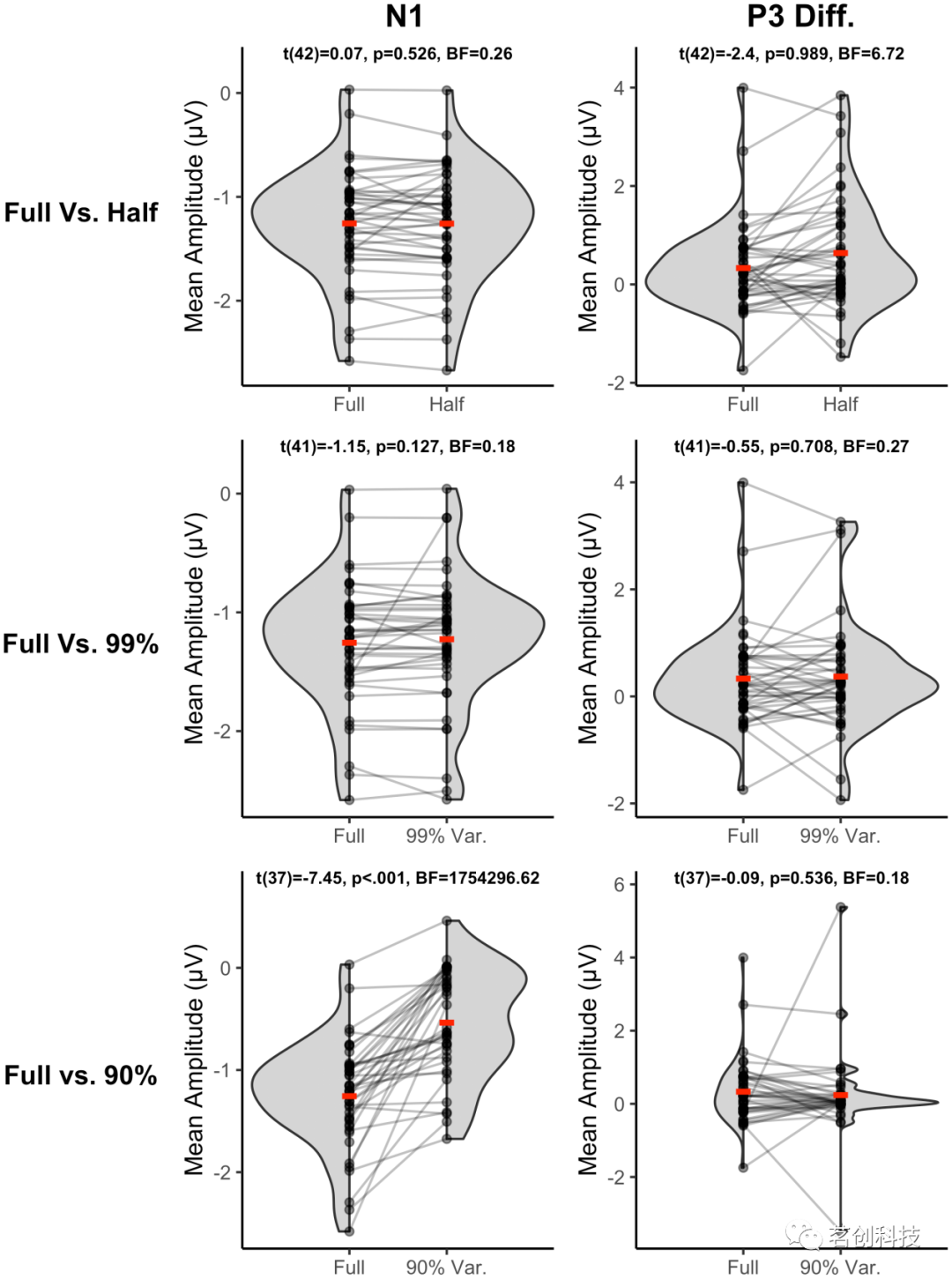
图2.降维ICA对N1和P3平均振幅的影响。灰点代表每个个体，灰线表示将不同条件的每个个体连接起来。红线表示均值。

平均振幅正态性和异常值的探索性分析。对平均振幅分布的目视检查表明，尽管每个分布的均值相对稳定，但降维条件(尤其是90%条件)导致了平均振幅分布的形状和异常值数量存在差异。为了评估rdICA是否导致更剧烈的正态偏离，对每种条件进行了探索性Anderson-Darling检验。该分析结果与rdICA一致，导致P3成分偏离正态性，其中90%的条件导致了最大的A统计量。另一方面，在进行多重比较校正后，N1平均振幅分布在任何条件下都没有显著偏离正态性。为了评估异常值，研究者使用PMCMRplus包中的gesdTest()函数，使用了广义极端学生化偏差(GESD)过程。该过程的结果基本上证实了图2所示的结果：基于PCA的rdICA导致P3成分产生了更多的异常值，但对N1则不然。

SME。图3描述了与图2相同的一组比较，只是将单个试次平均振幅的标准测量误差(SME)作为因变量。只有半维ICA导致了SME的预期增加，而99%和90%的条件导致了SME的明显下降。在所有条件比较中，贝叶斯因子都强烈支持N1 SME的备择假设；然而，只有full vs. half的差异符合预期(即，降维ICA导致较高的SME)。对于P3成分，full vs. 99%和full vs. 90%比较的贝叶斯因子表明，数据与零假设最一致：相对于全维数，P3 SME在99%或90%条件下没有显著变化。

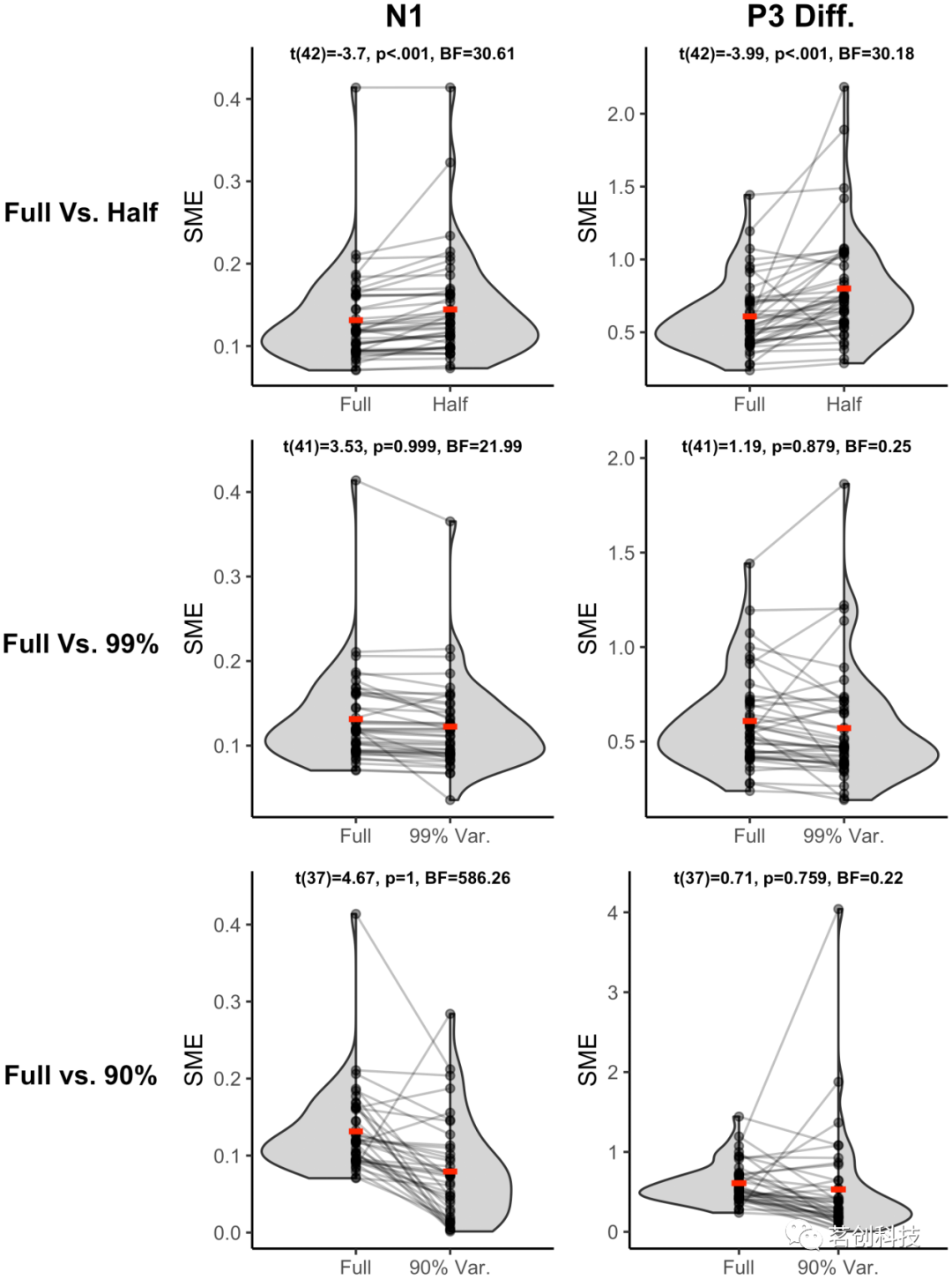
图3.降维ICA对N1和P3标准测量误差(SME)的影响。

信度。图4描述了N1和P3成分的原始和Spearman-Brown校正的分半信度。总的来说，N1的信度大于P3差异波的信度，这与已知的减法评分对信度的有害影响是一致的。令人惊讶的是，90%条件下的N1和P3成分最可靠。对于P3差异分数，full、half和99%条件的信度系数都落在90%条件系数的95%置信区间之外，因此90%条件的信度显著高于其他条件。然而，从散点图中可以看出，90%的条件在被试之间产生了更多的异质性，并产生了可能虚假夸大可靠性的外围数据点。

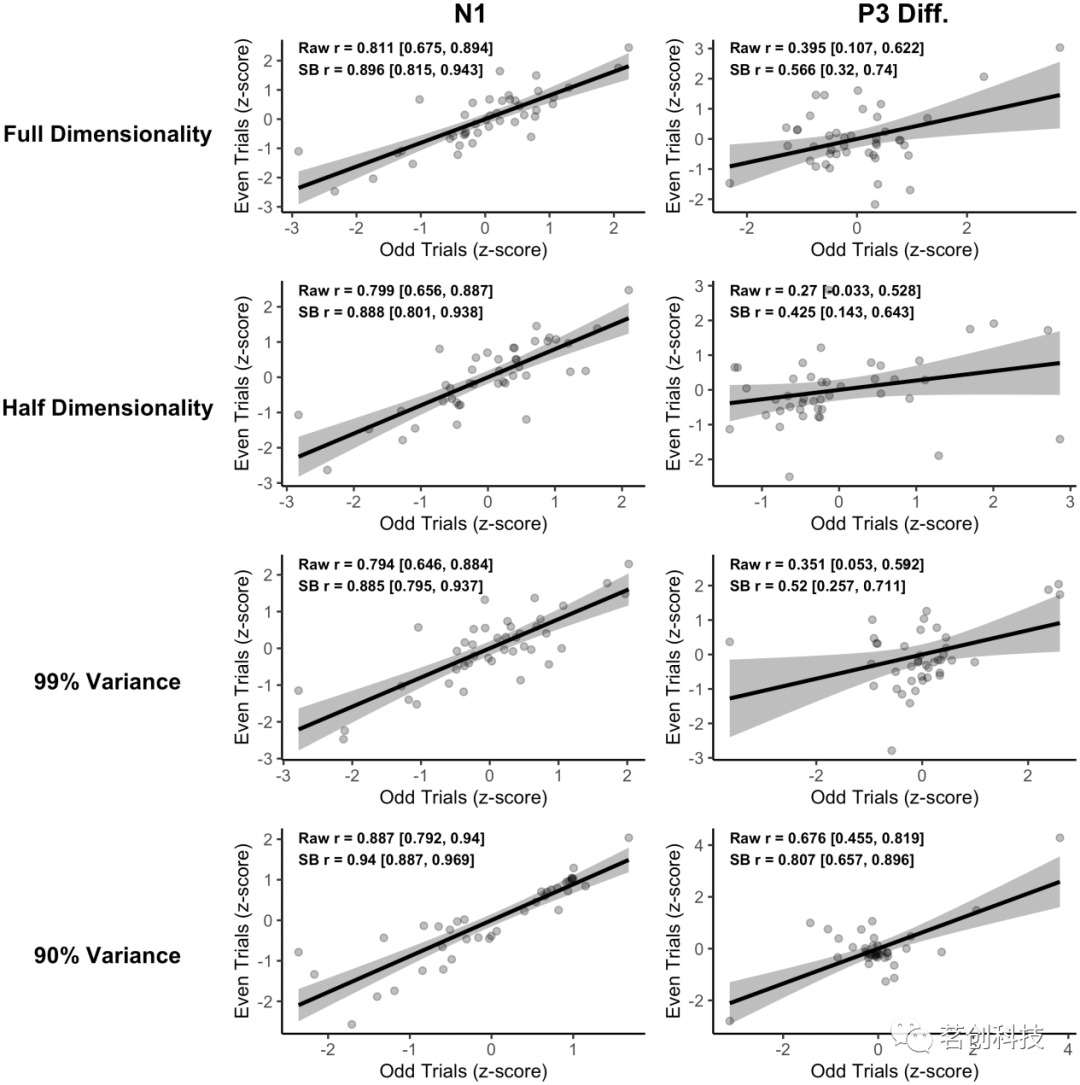
图4.降维ICA对N1和P3信度的影响。

混合ICs。为了阐明rdICA是否导致混合ICs的比例更高，图5比较了被IClabel标记为低置信度的ICs的方差占比(PVAF)(忽略其他标签分类的置信度)。总的来说，与其他条件相比，全维ICA与混合ICs的比例较小相关，尽管在99%和90%条件下的差异更大。

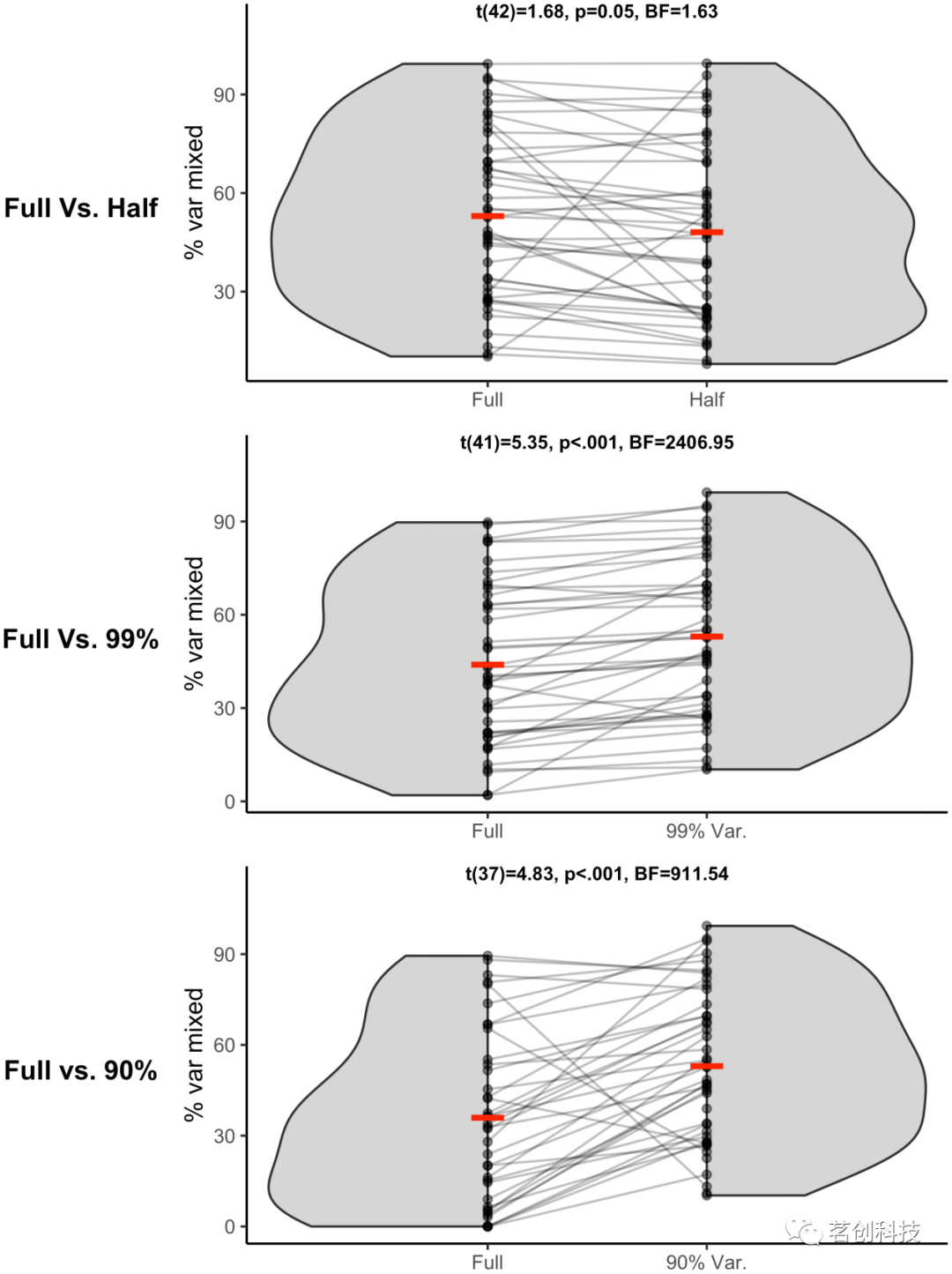
图5.用于rdICA的混合ICs比例的比较。

然后进行后续的中介分析，以检验与降维ICA相关的ERP数据质量下降是否是由于混合ICs的比例较高。结果发现，没有观察到混合ICs的比例介导了rdICA和数据质量之间关系的有力证据(见表1)。这表明，虽然在降维ICA中的混合ICs比例较高，但这种增加并不能有效地解释下游ERP数据质量的下降。

表1.ACME结果表。

验证数据集的信度系数也受到99%和90%条件下单个较大异常值的影响，导致P1成分的信度较差，而N2成分不受影响。在初步分析中，90%条件下的两个成分显示出最高的信度系数，而在验证数据集中90%条件下的P1成分显示出最差的信度系数。N2成分也受到这个异常值的影响。在这种情况下，信度系数就可能被高估了。与初步分析类似，90%和99%的条件与验证数据集中混合ICs比例的大幅增加有关。在这两个数据集中，半维条件与混合ICs比例的增加无关。最后，在验证数据集中再次观察到混合ICs比例缺乏中介效应。

结论

本研究旨在检验降维ICA对常见ERP成分的下游数据质量的影响。在大幅降维条件(90%)下，观察到早期感觉成分(P1和N1)的平均振幅存在显著的变化，但在其他条件或更晚的认知成分中(N2和P3)没有观察到这种差异。在半维条件下，所有成分的标准测量误差都较大，但在99%或90%条件下则不然。rdICA对分半信度的影响不太明显：在初步分析中，N1和P3的分半信度在90%条件下最高，而对于验证数据集，P1的分半信度在90%条件下最低，而N2的分半信度最高。最后，在降维条件下，混合ICs的比例通常更大，但这种增加并不能解释下游数据质量的变化。本研究提供了在ICA之前降低维数的最佳实践，并给出了以下建议：①rdICA的阈值通常应为99%或更高；②PCA阈值rdICA通常应该优先考虑可扩展性的情况(对于优先考虑可扩展性和处理速度的分析，只要阈值保持在99%或以上，PCA阈值ICA就可能是有价值的)；③对较少数量的电极进行分组会导致数据质量更差，因此不建议通过电极分组来提高计算效率；④如果选择使用基于PCA的rdICA策略，必须密切监测异常值。

总的来说，什么时候rdICA是合理的呢？根据观察到的数据，研究者认为基于PCA的rdICA需谨慎使用。事实上，当给定的EEG数据矩阵中存在线性相关时，通常先进行PCA再进行ICA。这种线性相关意味着数据矩阵中至少有一个通道不提供任何独立的信息(当来自两个相邻通道的凝胶桥接在一起时尤其常见)。幸运的是，数据矩阵的秩可以通过代数方法确定，然后使用PCA将矩阵化简为满秩状态。因此，在这种情况下，在ICA之前降低数据矩阵的维数是没有争议的，事实上，这是许ICA管道的常见过程！

相反，问题的关键似乎是：我们应该将给定数据矩阵的维数降低多少？本研究的发现与Artoni等人的发现一致，即PCA阈值低于99%往往会过于激进地降低维数，从而导致重要信息丢失或ICA没有足够的自由度来有效分离源信号。话虽如此，本研究结果表明，与全维数据相比，99%阈值PCA不太容易造成“过度减少”，下游数据质量也没有显著受损。因此，本研究认为，只要研究人员意识到降维可能存在的陷阱(例如，过度减少、异常值生成、可能偏离正态等)，rdICA可能不仅是合理的，而且对于提高运行速度和扩大心理生理学研究的范围至关重要。

用于预处理EEG的Matlab代码和用于后续统计分析的R代码可在以下网址获取：https://github.com/vpokorny123/Psychophys-rdICA。此外，包含主数据集和验证数据集的原始EEG文件可在以下位置找到：https://osf.io/jrb3q/。

参考文献：Victor J. Pokorny., Scott R. Sponheim., Eric Rawls. (2022). Impact of reduced-dimensionality independent components analysis on event-related potential measurements. Psychophysiology, 2022;00:e14223. DOI: 10.1111/psyp.14223