本文已收录于专栏 《算法合集》

---

---

一、简单释义

1、算法概念

  选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是：第一次从待排序的数据元素中选出最小 的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小元素，然后放到已排序的序列的末尾 。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。

2、算法目的

  从要排序的序列中，按指定的规则 (文中以升序为例)选出某一元素，再依规定交换位置后达到排序 的目的。  

3、算法思想

  每一趟从待排序的数据元素中选择最小的一个元素作为首元素 ，以此类推。直到所有元素排完为止。

二、核心思想

1. 先–在序列中找到最小元素，放到序列的起始位置作为已排序序列；
2. 中–从剩余未排序元素中继续寻找最小元素，放到已排序序列的末尾；
3. 后–重复上述步骤，直到所有元素均排序完成。

三、图形展示

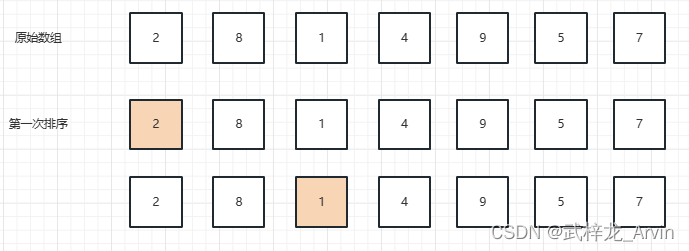
  1、第一次排序：用第一个元素和后面的元素进行对比，2和8对比，8比2大继续向后对比，然后2和1对比，1比2小，拿1继续向后比。此时我们可以发现后面没有比1小的值了。但是根据选择排序的原则，还是需要继续和剩下的元素进行比较的指导比较到7才能确定最小值。最终第一次排序的结果是1和2交换了位置。

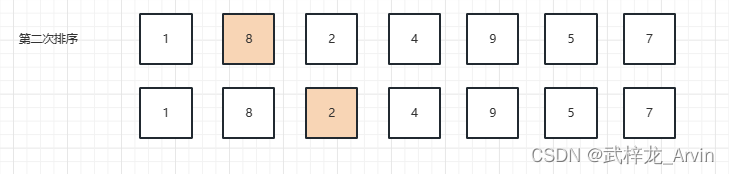
  2、第二次排序：目前1是已经排好序的了，所以1不参与任何的对比。用第二个元素8和后面的元素进行对比，8和2对比，2比8小，拿2和后面的元素进行对比。一直对比到7，才能确定2是最小的元素。最终第二次排序的结果是8和2交换了位置。

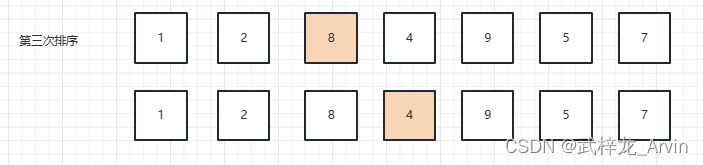
  3、第三次排序：用8和4进行对比，4比8小。把8放回。用4和后面的元素进行对比。4和9进行对比，4比9小，继续向后对比。4和5进行比较，4比5小，继续向后对比。4和7进行对比，4比7小，确定4是最小的元素。最终第三次排序的结果是8和4交换了位置。

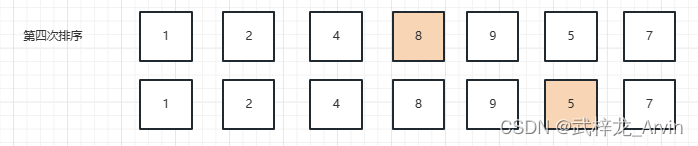
  4、第四次排序：用8和9进行对比，9比8大。继续向后对比。8和5进行比较，5比8小，用5和后面的元素进行对比。5和7进行对比，5比7小。确定5是最小的元素。最终第四次排序的结果是8和5交换了位置。

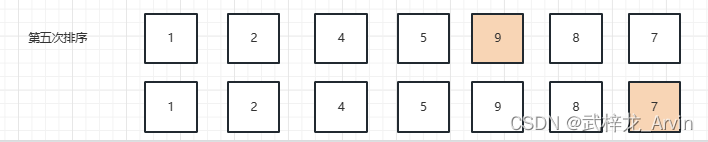
  5、第五次排序：按照上面的步骤，以此类推。第五次排序的结果是9和7交换了位置。

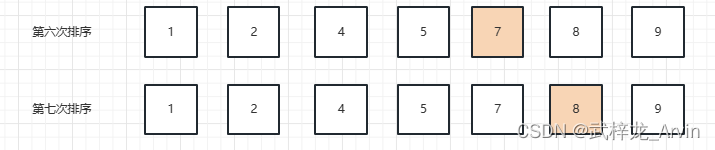
  6、第六、七次排序：第六次和第七次排序没有发生位置的交换。我们可以发现第五次的排序结果整个数组就已经是一个有序的数组的，但是选择排序算法还是进行了无用的排序错误。所以我们是可以优化算法的。

四、代码实现

1、优化之前

/**
 * @BelongsProject: demo
 * @BelongsPackage: com.wzl.Algorithm.DirectSelectionSort
 * @Author: Wuzilong
 * @Description: 选择排序
 * @CreateTime: 2023-04-28 11:25
 * @Version: 1.0
 */

public class DirectSelectionSort {
    public static void main(String[] args) {
        int[] numArray={2,8,1,4,9,5,7};
        //交换需要的中间量
        int temp;
        for (int i=0; i<numArray.length;i++){
            //定义最小值的变量
            int min=i;
            for (int j=i+1;j<numArray.length;j++){
                if (numArray[min]>numArray[j]){
                    //更新最小值的下标
                    min=j;
                }
            }
            temp=numArray[i];
            numArray[i]=numArray[min];
            numArray[min]=temp;
            System.out.println("第"+(i+1)+"轮插入"+Arrays.toString(numArray));
        }
    }
}

运行结果

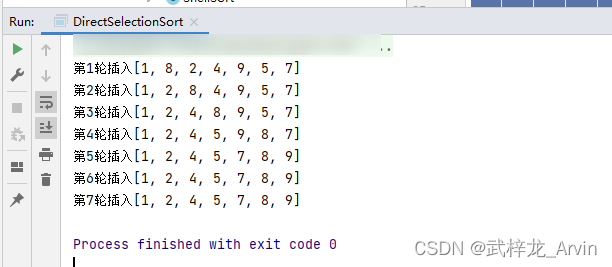
2、优化之后

/**
 * @BelongsProject: demo
 * @BelongsPackage: com.wzl.Algorithm.DirectSelectionSort
 * @Author: Wuzilong
 * @Description: 选择排序优化版
 * @CreateTime: 2023-04-28 11:25
 * @Version: 1.0
 */

public class DirectSelectionSort {
    public static void main(String[] args) {
        int[] numArray={2,8,1,4,9,5,7};
        //交换需要的中间量
        int temp;
        for (int i=0; i<numArray.length-1;i++){
            if( i == numArray.length-2){ //如果i=数组的最后两个值
                break;  //退出循环
            }
            //定义最小值的变量
            int min=i;
            for (int j=i+1;j<numArray.length;j++){
                if (numArray[min]>numArray[j]){
                    //更新最小值的下标
                    min=j;
                }
            }
            temp=numArray[i];
            numArray[i]=numArray[min];
            numArray[min]=temp;
            System.out.println("第"+(i+1)+"轮插入"+Arrays.toString(numArray));
        }
    }
}

运行结果

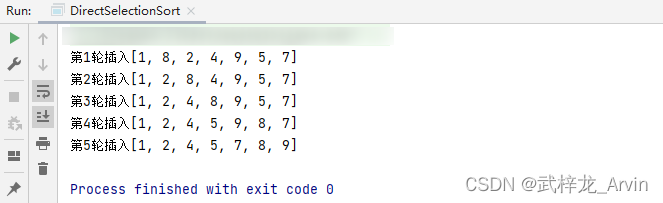
五、算法描述

1、问题描述

  给定一个 n 个元素的数组，数组下标从 0 开始，采用 选择排序 将数组按照 升序排列。

2、算法过程

整个算法过程分为以下几步：
  1）循环迭代变量 i = 0 → n − 1 i = 0 \to n-1i=0→n−1；
  2）每次迭代，令 m i n = i min = imin=i，j = i + 1 j = i+1j=i+1；
  3）循环执行比较 a [ j ]和 a [ m i n ] ，如果产生 a [ j ] < a [ m i n ] 则执行 m i n = j 执行 j = j + 1，继续执行这一步，直到 j = = n；
  4）交换 a [ i ] a[i]a[i] 和 a [ m i n ] a[min]a[min]，回到 1）。

六、算法分析

1、时间复杂度

  最好的情况全部元素已经有序，则 交换次数为0；最差的情况，全部元素逆序，就要交换 n-1 次；所以最优的时间复杂度和最差的时间复杂度和平均时间复杂度 都为 ：O(n^2)

2、空间复杂度

  最优的情况下（已经有顺序）复杂度为：O(0) ；
  最差的情况下（全部元素都要重新排序）复杂度为：O(n );
  那么选择排序算法平均的时间复杂度为：O(1)

3、算法稳定性

  选择排序是给每个位置选择当前元素最小的，比如给第一个位置选择最小的，在剩余元素里面给第二个元素选择第二小的，依次类推，直到第n-1个元素，第n个元素不用选择了，因为只剩下它一个最大的元素了。那么，在一趟选择，如果一个元素比当前元素小，而该小的元素又出现在一个和当前元素相等的元素后面，那么交换后稳定性就被破坏了。所以选择排序是不稳定的。

🎯 此文章对你有用的话记得留言+点赞+收藏哦🎯