Pytorch nn.Softmax(dim=?) 详解

news2024/7/4 4:28:41

本文参考自：Pytorch nn.Softmax(dim=?) - 知乎

原文写得很好了，我这边另外完善了一些细节，让大家理解地更加直白一些。

可以先去看上面的参考文章，也可以直接看我这篇。

1、tensor1

1）已知该矩阵的维度为（2,2,2,3），我们可以用（d0,d1,d2,d3）来表示（2,2,2,3）。

2）当dim=0时

3）当dim=1时

4）当dim=2时

5）当dim=3时

2、tensor2

1）已知该tensor的维度为（3,3），那么d0=3,d1=3。

2） dim=0时

3）dim=1时

1、tensor1

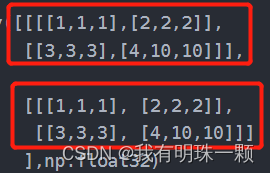
a = np.asarray([[[[1,1,1],[2,2,2]],
                [[3,3,3],[4,10,10]]],

                [[[1,1,1], [2,2,2]],
                 [[3,3,3], [4,10,10]]]
                ],np.float32)
print(a.shape)  #(2, 2, 2, 3)

1）已知该矩阵的维度为（2,2,2,3），我们可以用（d0,d1,d2,d3）来表示（2,2,2,3）。

接下来分情况讨论以下运算：

input = torch.from_numpy(a)

m0 = nn.Softmax(dim=0)  # dim=0的情况
output0 = m0(input)
print("output0: ",output0)

m1 = nn.Softmax(dim=1)  # dim=1的情况
output1 = m1(input)
print("output1: ",output1)

m2 = nn.Softmax(dim=2)  # dim=2的情况
output2 = m2(input)
print("output2: ",output2)

m3 = nn.Softmax(dim=3)  # dim=3的情况
output3 = m3(input)
print("output3: ",output3)

2）当dim=0时

我们将整个矩阵划分为d0=2份。每一份里面对应位置的d0=2个数进行softmax运算。

以此类推。

softmax函数的输出不改变原数据维度的大小，最后得到的是

3）当dim=1时

我们将整个矩阵划分为d0=2份（红色框）的基础上，再在这2个区域内分别划分出的d1=2个区域（黄色框），在更小的区域之间的d1=2个数之间进行softmax运算。

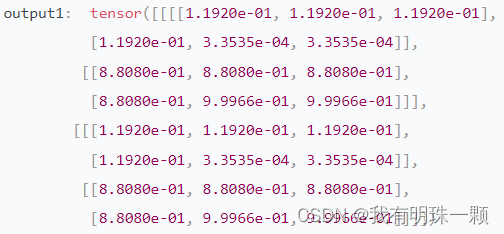
4）当dim=2时

我们将整个矩阵划分为d0=2份（红色框）的基础上，再在小区域内分别划分出的d1=2个区域（黄色框），再在更小的区域内划分出d2=2个区域（蓝色框），之后在相邻的最小区域（蓝色框）之间的d2=2个数之间进行softmax运算。

5）当dim=3时

我们将整个矩阵划分为d0=2份（红色框）的基础上，再在小区域内分别划分出的d1=2个区域（黄色框），再在更小的区域内划分出d2=2个区域（蓝色框），最后再划分出d3=3个最小区域（绿色框），区域之间的d3=3个数之间进行softmax运算。（简单说就是相邻3个绿色框内的数进行softmax运算）

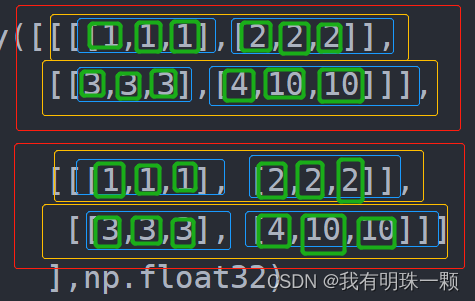
有了这个d0,d1,d2,d3...的维度说明之后，我们可以去理解任意一个tensor的Softmax运算，万变不离其宗。

2、tensor2

这里再举一个简单的例子：

x = torch.tensor([[0.7459, 0.5881, 0.4795],
                  [0.2894, 0.0568, 0.3439],
                  [0.6124, 0.7558, 0.4308]])
x_softmax = nn.Softmax(dim=0)(x)  # 每列算
print(x_softmax)
x_softmax2 = nn.Softmax(dim=1)(x)  # 每行算
print(x_softmax2)