在牛客网和leetcode等网站刷题的过程中,时常会遇到一些使用双指针和三指针解决问题的实例。今天,我来介绍这两种方法,相信你会对指针的应用会提高一个档次。
目录
- 移除元素
- 删除有序数组中的重复项
- 合并两个有序数组
在下面的讲解的过程中,我会以leetcode里的题目为例子,采用双指针和三指针方法进行实现,如果有其他实现方法,我也会写出来,与双指针和三指针进行比较。
注意,leetcode上是按照的核心代码的形式进行答题的,但是在下面的讲解的过程中,我主要以在vs2010编辑器书写所有的代码的形式进行讲解,leetcode里的题目只是作为引入。
移除元素

题目链接
在这里,题目的要求是返回删除元素后数组的元素新长度,我修改一下,直接打印出修改完的数组的元素
假设,数组元素为0,1,2,2,3,0,4,2,我要删除元素大小为2的所有元素。
不使用指针的方法
首先选择采用不使用指针的方法。
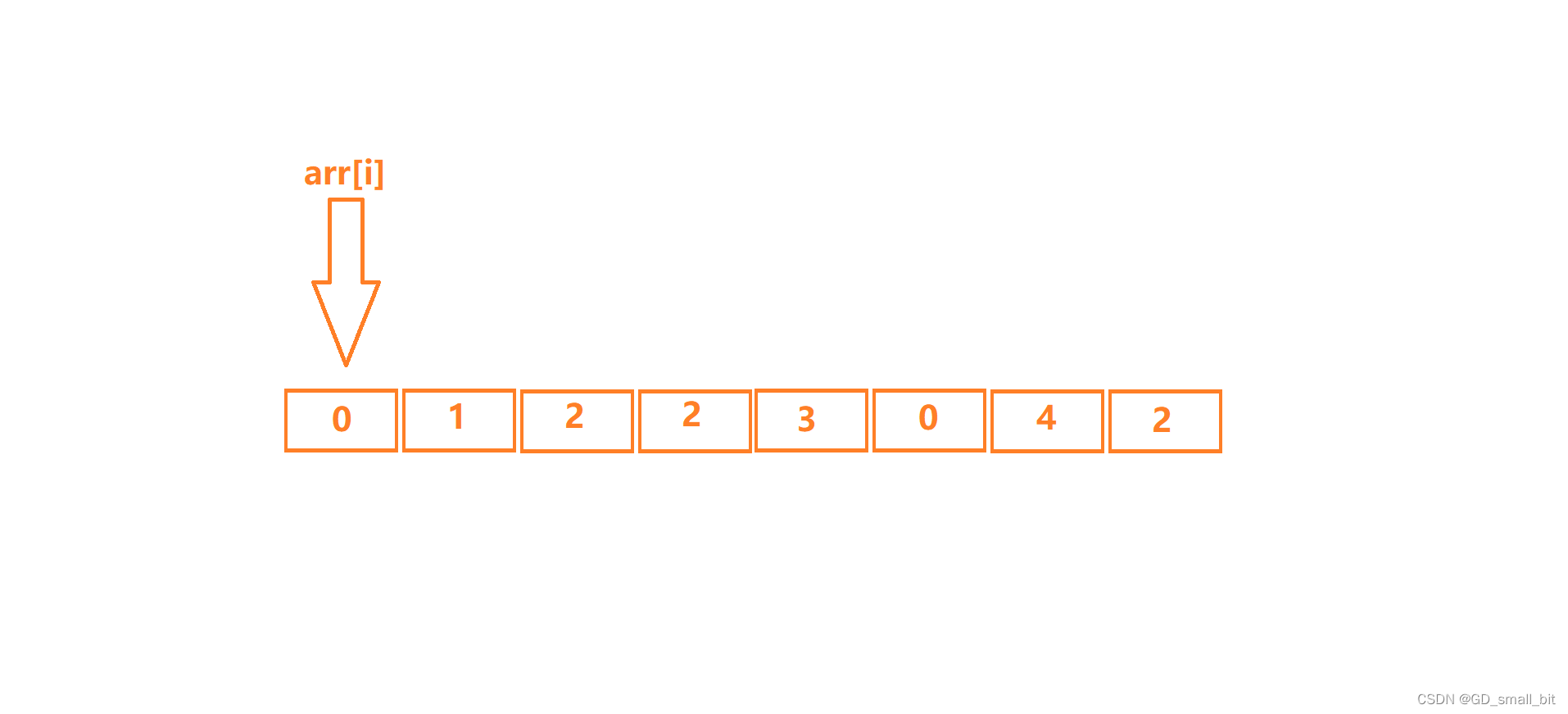
我定义变量i,让i从0开始,增大到为数组长度减一,让arr[i]遍历一遍数组。
如果在期间寻找到与要删除的数字相同的元素时,如:
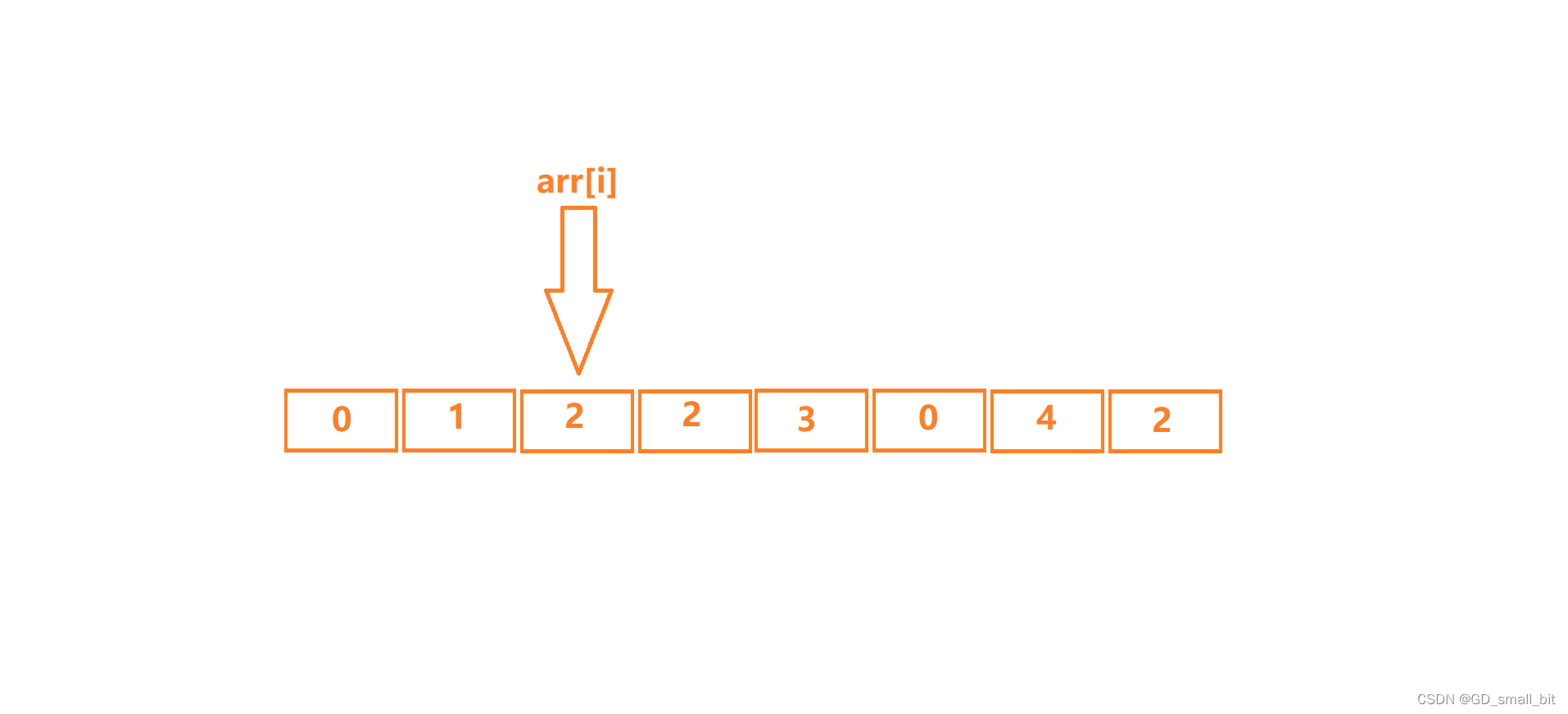
arr[i]找到元素时,此时的arr[i]等于要删除的数字,那么我就让后面的数字依次往前替换,同时,数组的长度减一。

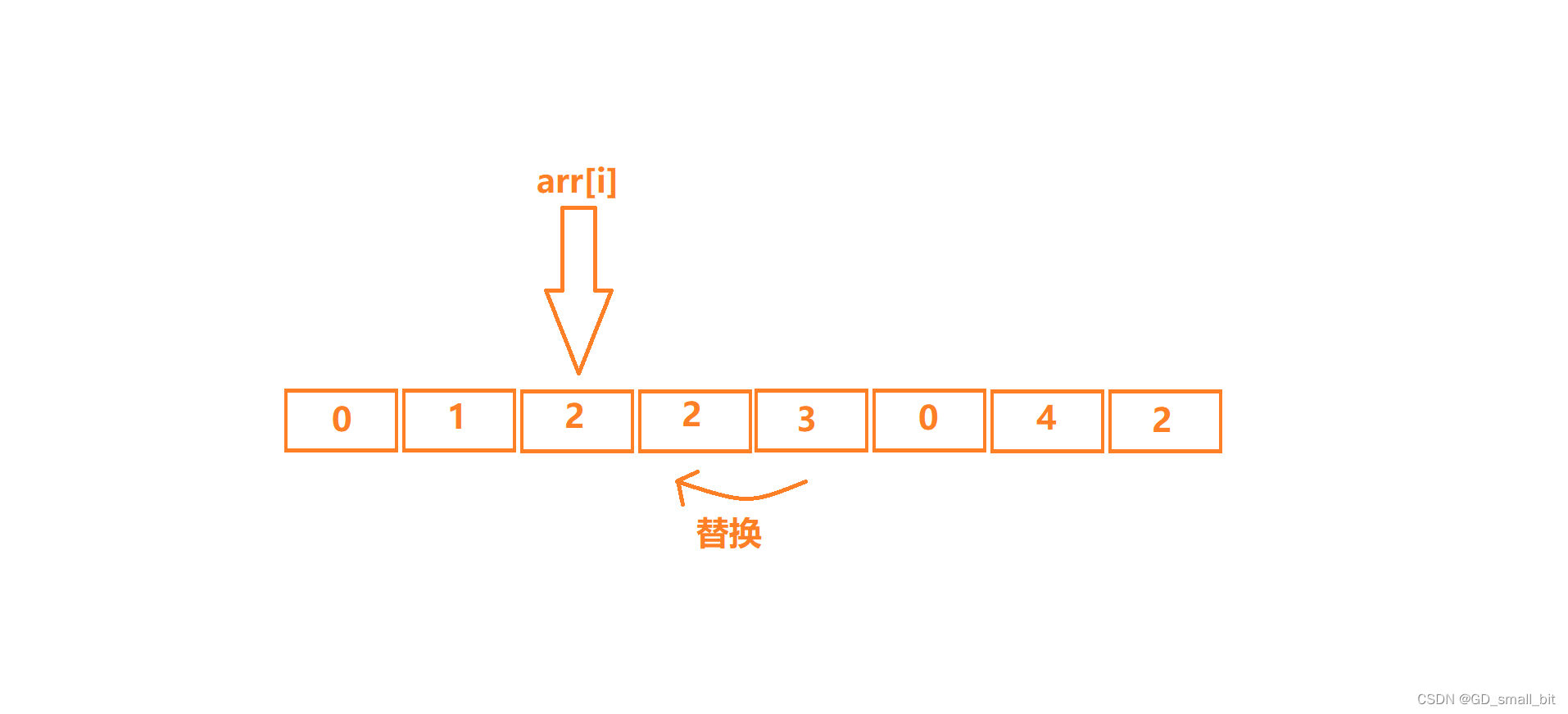

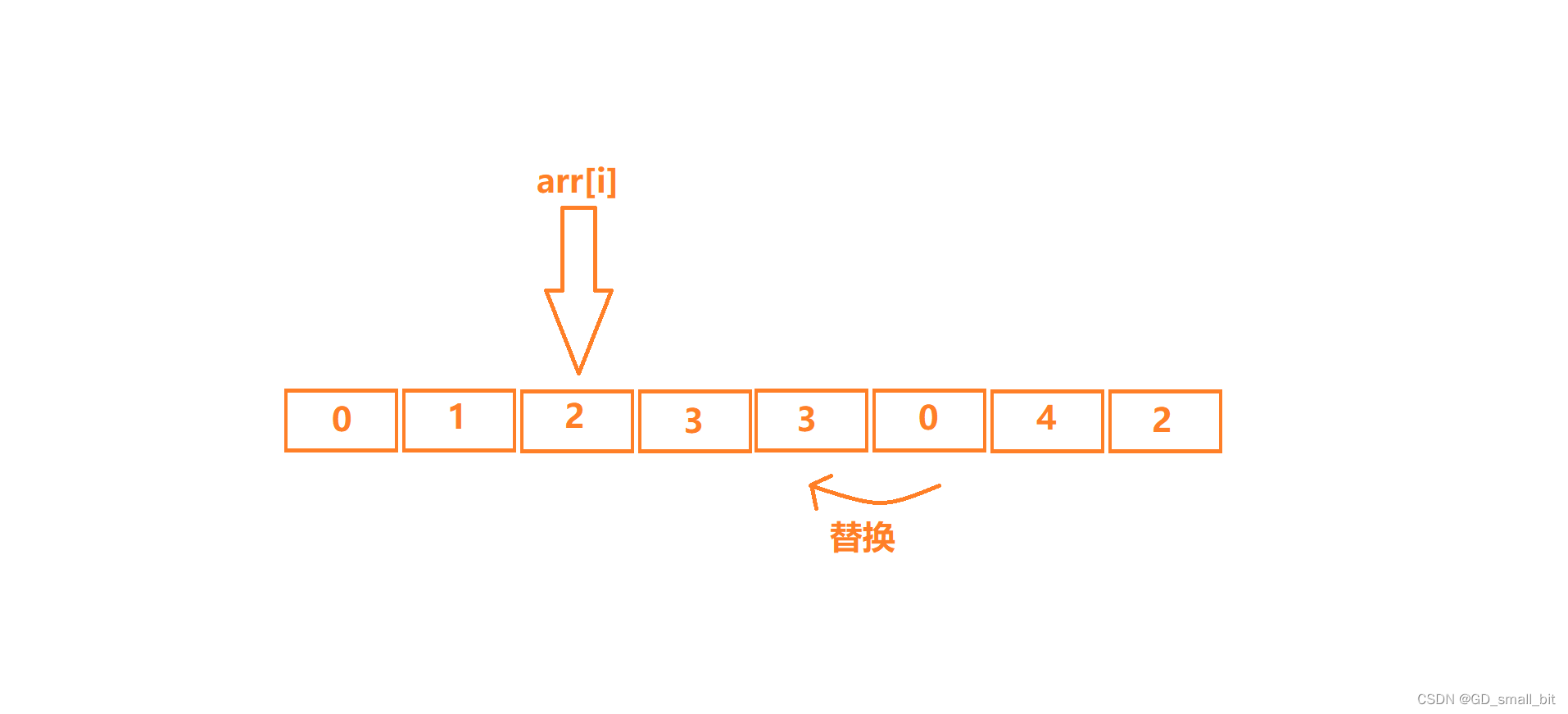
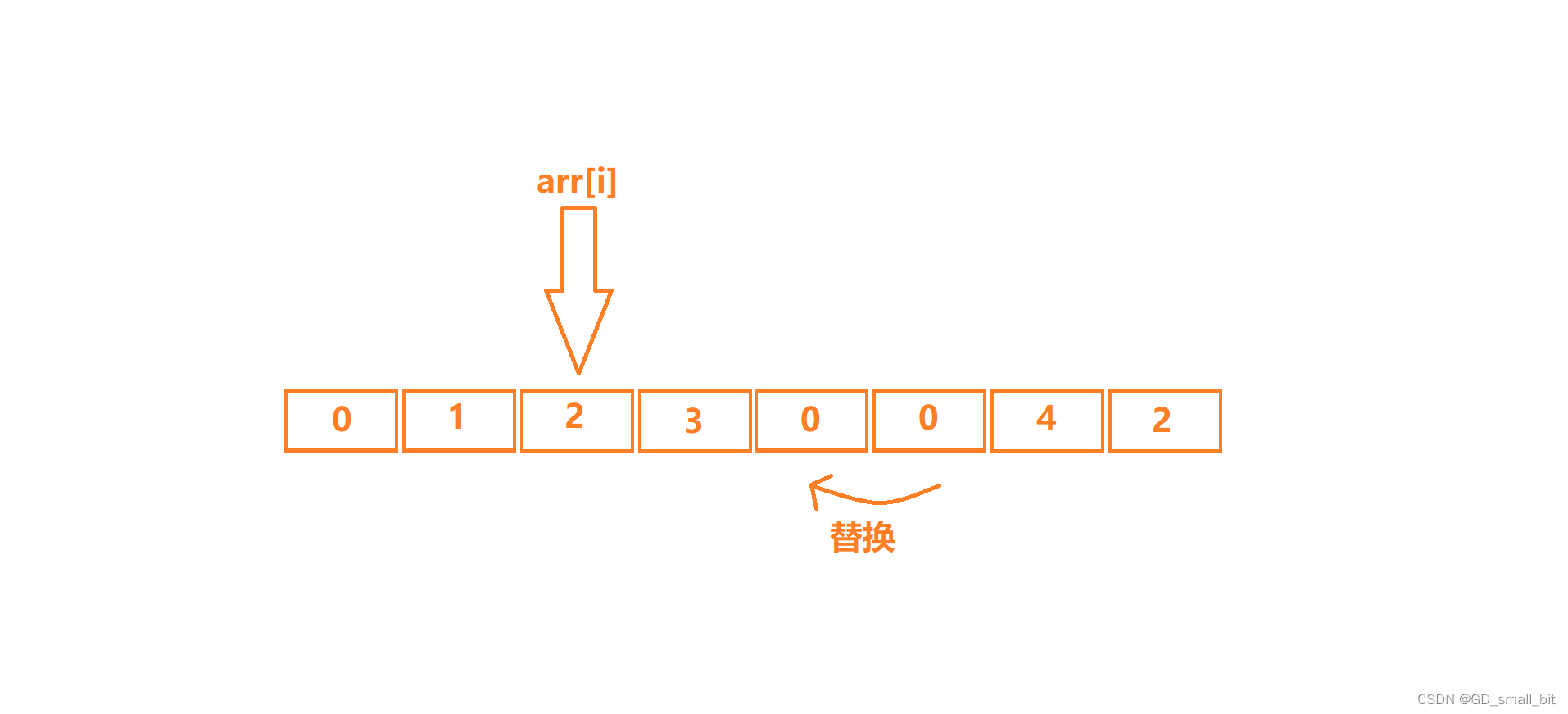
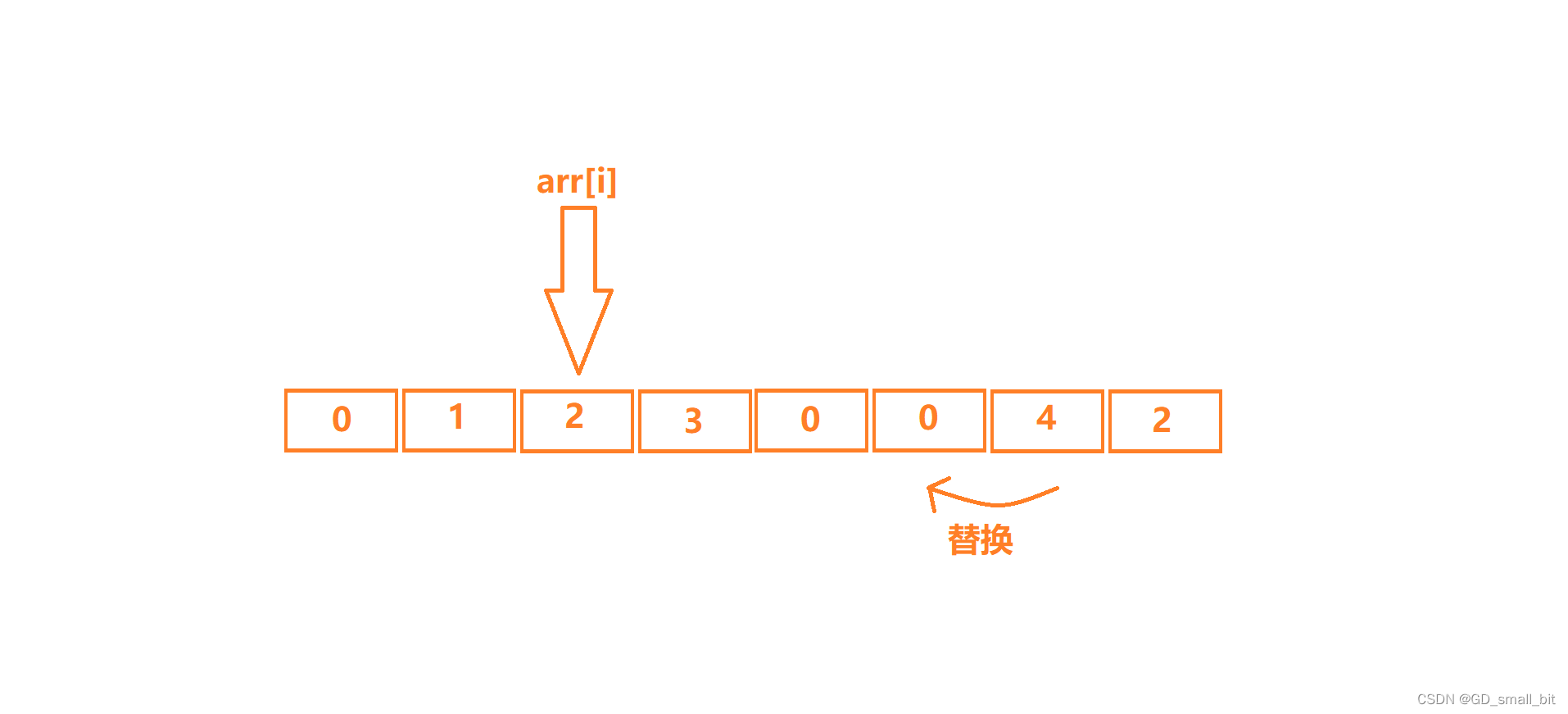
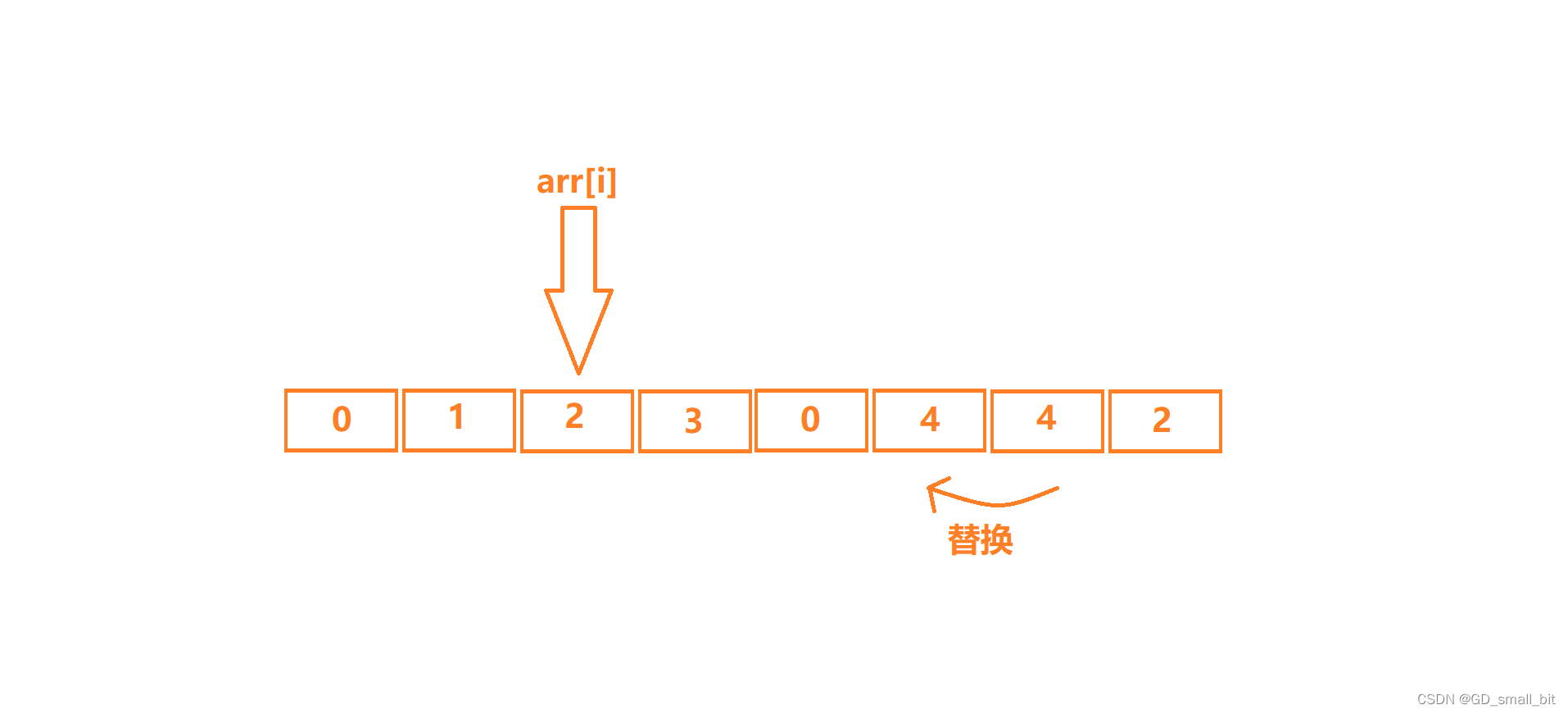
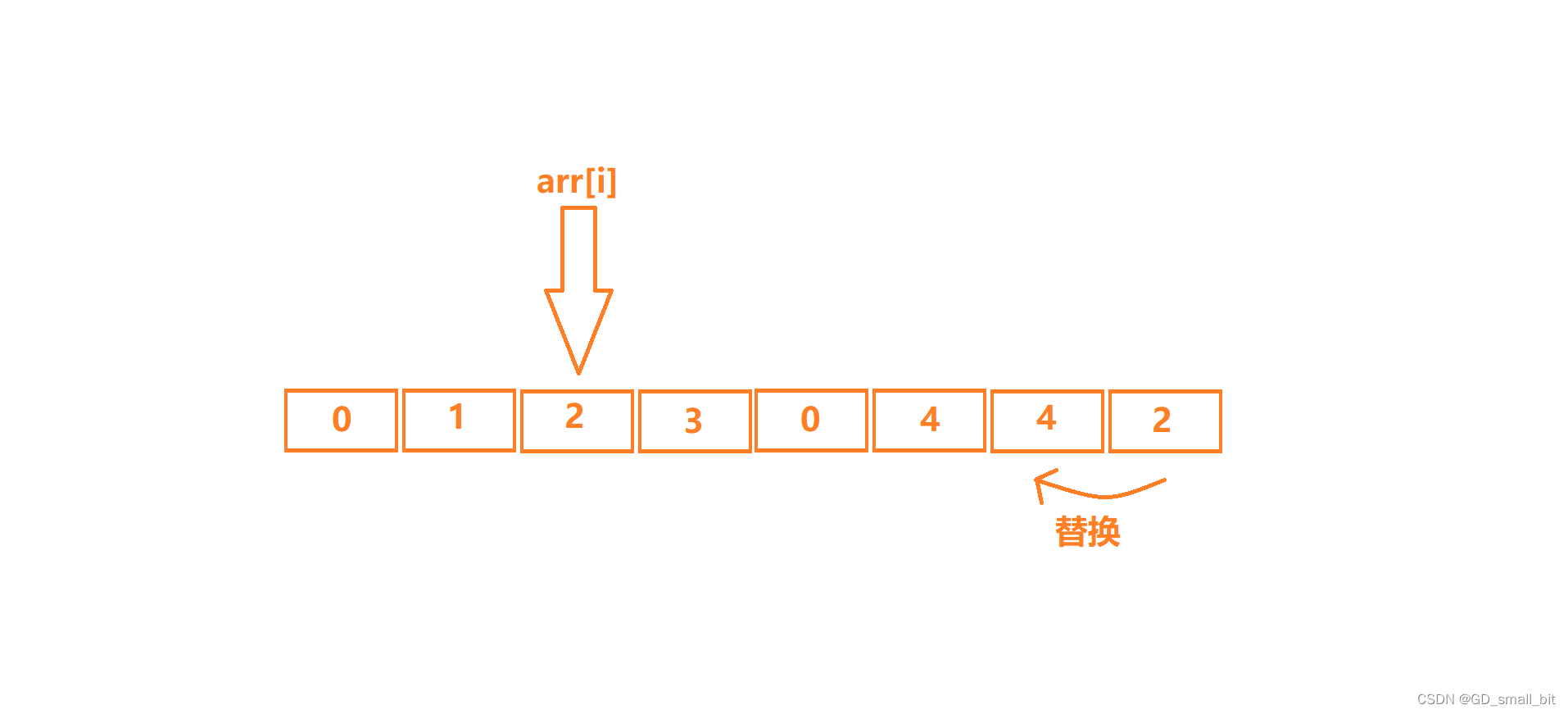
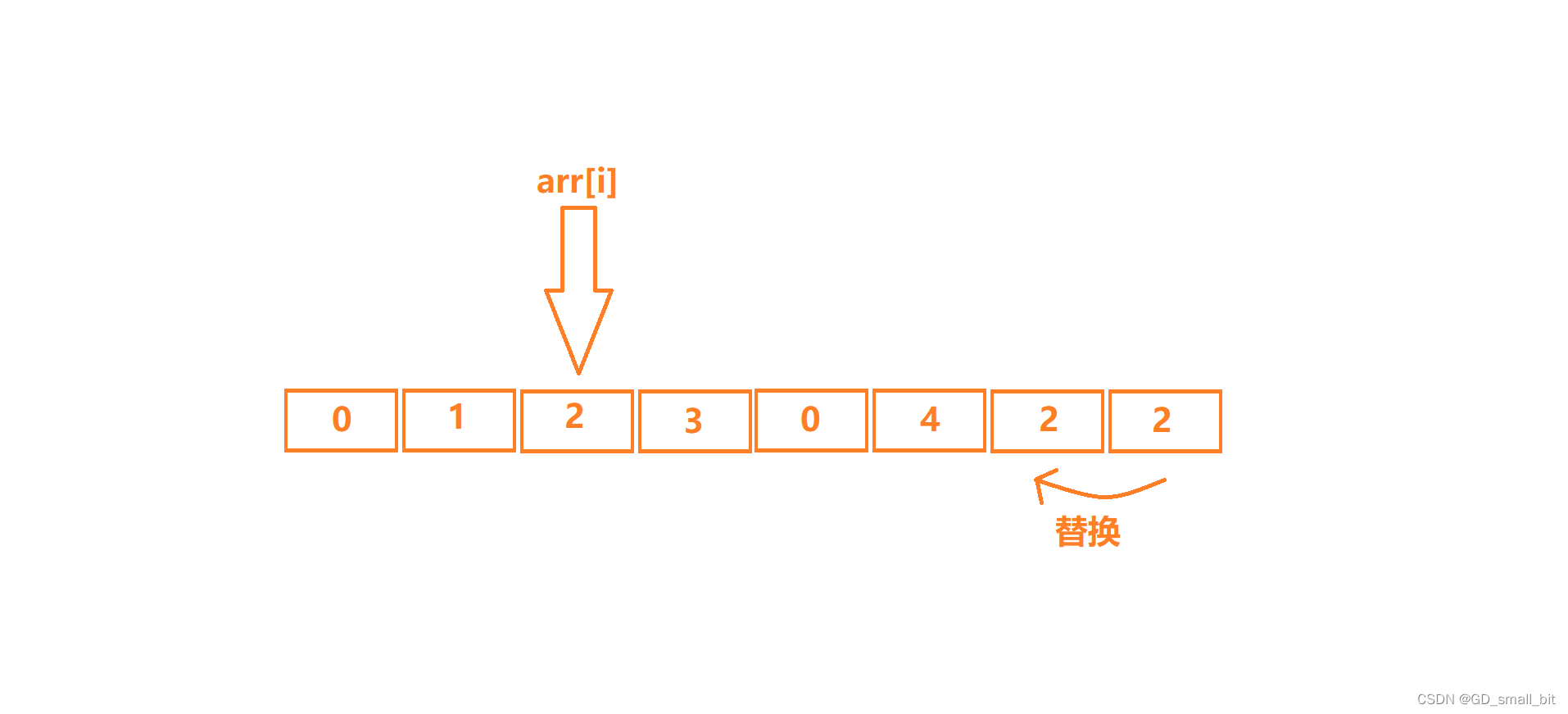
最后数组的长度减一。(因为最后一个元素也已经被拷贝到前面去了)。
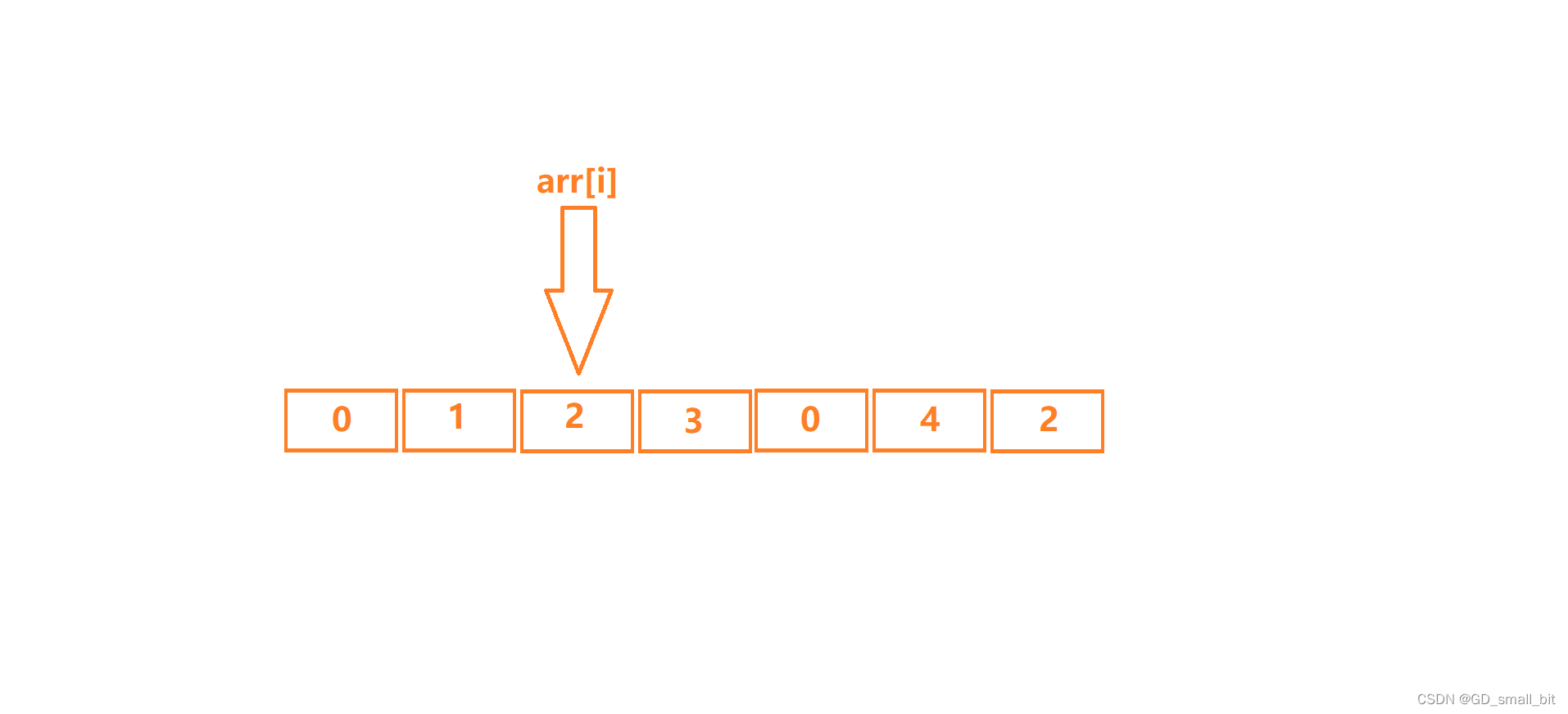
观察可以发现,刚才的2的元素已经被覆盖掉了,但是由于向前覆盖,arr[i]现在的位置又出现了一个2,这里就有一个小技巧,当arr[i]是要删除的数字时,覆盖以后,i不进行增加,让程序再次检查arr[i]的位置。
代码的实现如下:
#include<stdio.h>
void print(int arr[],int len) //打印函数
{
int i = 0;
for(i = 0; i < len; i++)
{
printf("%d ",arr[i]);
}
printf("\n");
}
int main()
{
int arr[] = {0,1,2,2,3,0,4,2}; //需要进行删除的数组
int val = 2; //需要删除的元素大小
int i = 0;
int j = 0;
int len = sizeof(arr)/sizeof(arr[0]);
while(i < len) //下标要小于数组的元素个数
{
if(arr[i] == val) //数组元素等于要删除的元素大小
{
j = i; //利用j值进行移动,防止i值的改变
while(j < len-1)
{
arr[j] = arr[j+1]; //往前替代
j++;
}
len--; //数组的长度减一
}
else
{
i++; //数组元素不等于要删除的元素大小,i值加一,arr[i]向后寻找
}
}
print(arr,len);
return 0;
}
运行结果如下:
由运行结果可知,该代码满足了我们的要求,但是代码满足要求就足够了吗?
这串代码的时间复杂度是:O(N^2)
空间复杂度是:O(1)
接下来,我来使用另外一种方法。
采用创建新数组和使用双指针的方法
如图,我创建一个新数组。

接下来,让指针src和指针dest分别指向原数组和新数组。
如果指针src指向的元素不是2时,将指针src指向的内容赋值到指针dest指向的空间。
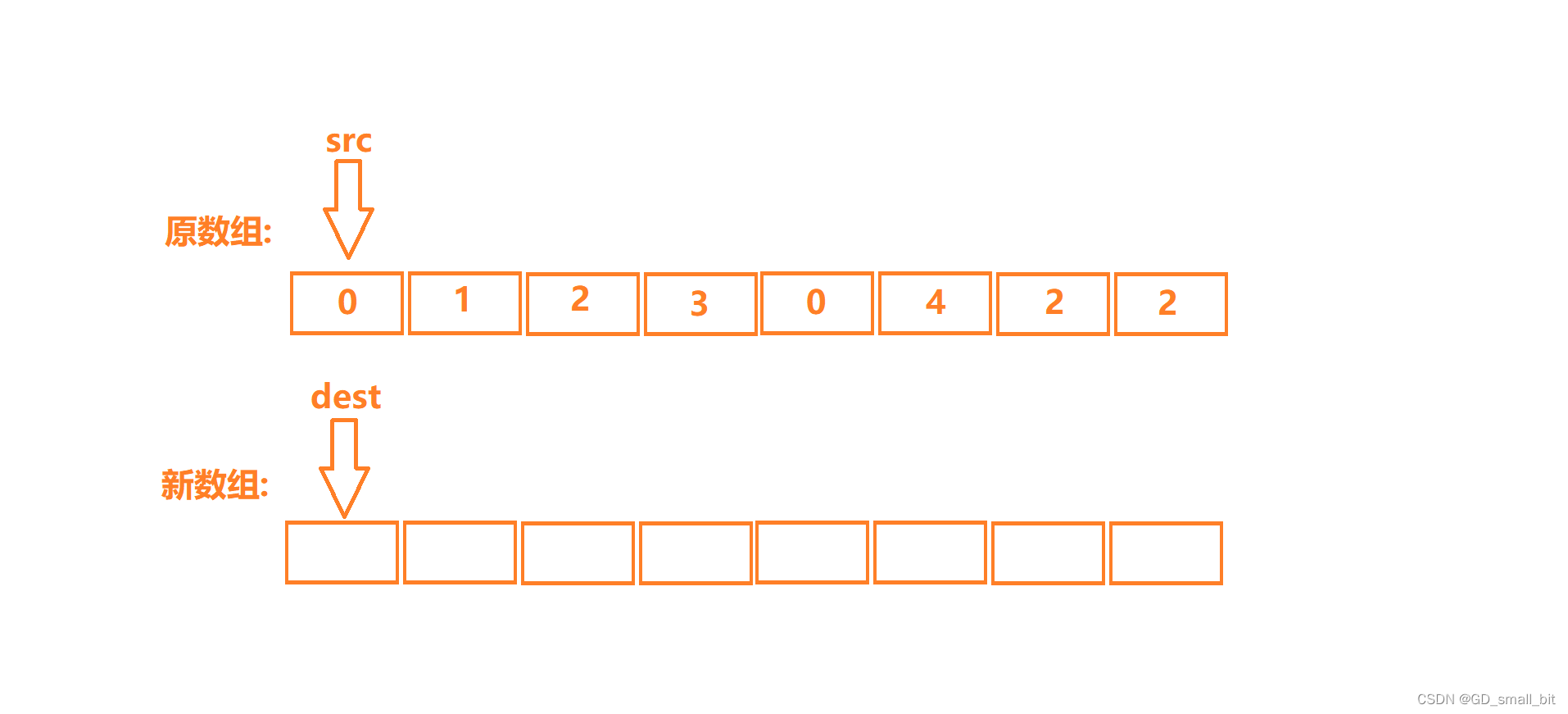
代码的实现如下:
#include<stdio.h>
void print(int arr[],int len) //打印函数
{
int i = 0;
for(i = 0; i < len; i++)
{
printf("%d ",arr[i]);
}
printf("\n");
}
int main()
{
int arr[] = {0,1,2,2,3,0,4,2}; //需要进行删除的数组
int arr1[20] = {0};
int val = 2; //需要删除的元素大小
int* src = arr;
int* dest = arr1;
int i = 0;
int j = 0;
int len = sizeof(arr)/sizeof(arr[0]);
while(i < len)
{
if(*(src + i) != val) //指针(src+i)不等于val时,赋值到指针(dest+i)指向的空间,i++,j++
{
*(dest + j) = *(src + i);
i++;
j++;
}
else //指针(src+i)等于val时,i++,找到下一个元素
{
i++;
}
}
print(arr1,j); //打印arr1数组中的j个元素
return 0;
}
运行结果如下:

由该运行结果可以得知,该代码依然可以满足我们的要求,现在,我来研究该代码的效率。
这串代码的时间复杂度是O(N)
空间复杂度是O(N)
显然,这一串代码是空间换取时间的典型例子,但是双指针的优点还是没有完全发挥出来,接下来,我来实现另外的一种代码,完全发挥出双指针的优点。
使用双指针
我定义两个指针,分别是指针src和指针dest,开始的时候,这两个指针都指向了数组的第一个元素。
接下来,我需要遍历一次数组,如果指针src指向的内容等于要删除数字的值的话,指针src向后走一步,如果指针src指向的内容不等于要删除数字的值的话,那么将指针src指向的内容赋值到指针dest指向的内容,并且两个指针向后走一步。
#include<stdio.h>
void print(int arr[],int len) //打印函数
{
int i = 0;
for(i = 0; i < len; i++)
{
printf("%d ",arr[i]);
}
printf("\n");
}
int main()
{
int arr[] = {0,1,2,2,3,0,4,2}; //需要进行删除的数组
int arr1[20] = {0};
int val = 2; //需要删除的元素大小
int* src = arr;
int* dest = arr1;
int i = 0;
int j = 0;
int len = sizeof(arr)/sizeof(arr[0]);
while(i < len)
{
if(*(src + i) != val) //指针(src+i)不等于val时,赋值到指针(dest+i)指向的空间,i++,j++
{
*(dest + j) = *(src + i);
i++;
j++;
}
else //指针(src+i)等于val时,i++,找到下一个元素
{
i++;
}
}
print(arr1,j); //打印arr1数组中的j个元素
return 0;
}
运行结果如下:

由运行结果可以得知,该串代码符合我们的要求。
这串代码的时间复杂度:O(N)
空间复杂度:O(N)
删除有序数组中的重复项

题目链接
假设在数组元素为0,0,1,1,1,2,2,3,3,4,我要删除一些重复的数组,并且只留下其中一个。
去重算法
使用两个指针src和dest,开始时都指向数组的第一个元素,如果两个指针src和dest的内容相等的话,那么指针src向后走一步,如果两个指针src和dest的内容不相等的话,就将指针src指向的内容赋值到指针dest指向的后面一步的空间。
代码的实现如下:
#include<stdio.h>
void print(int arr[],int len) //打印函数
{
int i = 0;
for(i = 0; i < len; i++)
{
printf("%d ",arr[i]);
}
printf("\n");
}
int main()
{
int arr[] = {0,0,1,1,1,2,2,3,3,4};
int* src = arr; //指针src存储数组首元素的地址
int* dest = arr; //指针dest存储数组首元素的地址
int i = 0;
int j = 0;
int len = sizeof(arr)/sizeof(arr[0]);
while(i < len) //i要小于数组长度,不用判断j,因为i肯定会先达到大于数组长度的条件
{
if(*(dest + j) == *(src + i)) //如果两个指针指向的内容相等,src指针要向后走一步,i++可以实现该效果
{
i++;
}
else //如果两个指针指向的内容不相等,dest指针向后走一步。src指针指向的内容赋值到指针dest指向的内容,然后i++
{
j++;
*(dest + j) = *(src + i);
i++;
}
}
print(arr,j + 1);
return 0;
}
运行结果如下:

由运行结果可以得知,该代码符合我们的要求。
观察可以发现,去重算法依然是以双指针为基础,进行操作的,可见双指针运用的广泛。
这串代码的时间复杂度是:O(N)
空间复杂度是:O(1)
合并两个有序数组
在这道题中,有两个版本,一个较为简单,一个较为难。leetcode上这一道题是难的版本,而我要先讲解简单版本。
题目要求:给你两个按递增顺序排列的整数数组nums1 和nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 和 nums1 ,使合并后的数组同样按递增进行排列。
假设nums1的数组元素是1,2,3,5,6,9,nums2的元素是2,5,6。
我依然采用双指针的方法,先创建一个新数组和两个指针,第一个指针指向nums1的第一个元素,第二个指针指向nums2的第一个元素,比较这两个指针指向的内容谁大谁小,小的就赋值到新数组。
然后继续遍历,直到数组nums1和数组nums2的元素都已经被赋值到新数组中。
代码的实现如下:
#include<stdio.h>
void print(int arr[],int len) //打印函数
{
int i = 0;
for(i = 0; i < len; i++)
{
printf("%d ",arr[i]);
}
printf("\n");
}
int main()
{
int arr1[] = {1,2,3,5,6,9};
int arr2[] = {2,5,6};
int arr[20] = {0}; //创建新数组
int* src1 = arr1; //创建一个指针指向数组arr1的首元素地址
int* src2 = arr2; //创建一个指针指向数组arr2的首元素地址
int i = 0;
int j = 0;
int k = 0;
int len1 = sizeof(arr1)/sizeof(arr1[0]);
int len2 = sizeof(arr2)/sizeof(arr2[0]);
while(i < len1 && j < len2) //i值和j值分别小于数组对应长度,就进入循环
{
if(*(src1 + i) < *(src2 + j)) //*(src1 + i)指向的元素较小,将*(src1 + i)赋值到新数组中
{
arr[k] = *(src1 + i);
k++; //k++,保证赋值到新数组的下一个位置
i++; //i++,保证被复杂过的元素不再被复制
}
else
{
arr[k] = *(src2 + j); //*(src2 + j)指向的元素较小,或者两个指针指向的元素相等(复制哪个指针的内容都可以),将*(src2 + j)的元素赋值到新数组
k++; //k++,保证赋值到新数组的下一个位置
j++; //j++,保证被复制过的元素不再被复制
}
}
if(j >= len2) //当*(src2 + j)走完arr2数组,而*(src1 + i)还没有走完arr1数组的情况
{
while(i < len1)
{
arr[k] = *(src1 + i);
k++;
i++;
}
}
if(i >= len1) //当*(src1 + i)走完arr2数组,而*(src2 + j)还没有走完arr2数组的情况
{
while(j < len2)
{
arr[k] = *(src2 + j);
k++;
j++;
}
}
print(arr,k);
return 0;
}
运行结果如下:
由运行结果可以得知,此串代码符合我们的要求。
这串代码的时间复杂度是O(N)
空间复杂度是O(N)
接下来,我来实现较难的版本,注意在这一道题中,两个版本的题目是不一样的,所以时间复杂度和空间复杂度不做比较。
题目要求:给你两个按递增顺序排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按递增顺序排列。
题目链接
假设第一个数组的元素是:1,2,3,0,0,0,第二个数组的元素是2,5,6,第一个数组后面留三个是给第二个数组的元素留的位置,所以第一个数组只看前三个元素,是递增顺序的。
在这一版本中,不再要求我们合并到一个新的数组,而是要合并到第一个数组中,并且还要按照递增的顺序进行排列。
那么,在这一版本中,就要引入三指针的方法。
先定义三个指针分别是src1、src2、dest,指针src1指向第一个数组递增顺序中的最后一个元素(也就是3)。指针src2指向第二个数组的最后一个元素,也就是6,指针dest指针指向第一个数组最后一个元素(包括非顺序的),如下:
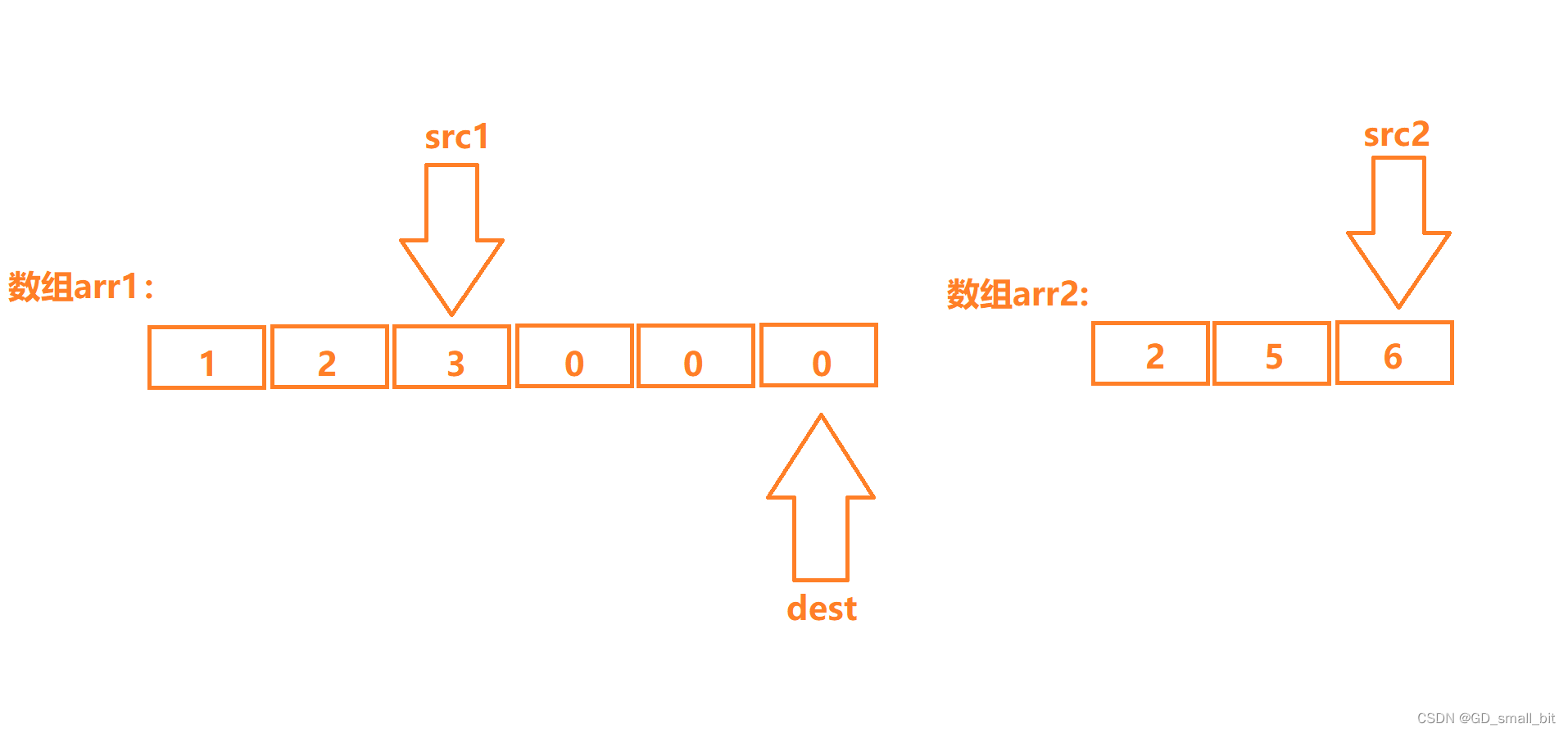
接下来,比较指针src1和指针src2指向的内容,哪个指针指向的内容大时,就赋值到指针dest指向的空间处,并且该指针和指针dest向前走一步。
代码的实现如下:
#include<stdio.h>
void print(int arr[],int len) //打印函数
{
int i = 0;
for(i = 0; i < len; i++)
{
printf("%d ",arr[i]);
}
printf("\n");
}
int main()
{
int arr1[] = {1,2,3,0,0,0};
int arr2[] = {2,5,6};
int len1 = sizeof(arr1)/sizeof(arr1[0]);
int len2 = sizeof(arr2)/sizeof(arr2[0]);
int* str1 = arr1;
int* str2 = arr2;
int* dest = arr1;
int i1 = len1 - len2 - 1; //让arr1加该值,len1的值为6,len2的值为3,len1减len2得到3,3再减一得到2,arr是数组首元素地址,arr+2找到3的位置
int i2 = len2 - 1; //让arr2加该值,找到数组arr2的最后一个元素
int j = len1 - 1; //让arr1加该值,找到数组arr1的最后一个元素
while(i1 >= 0 && i2 >= 0) //i1和i2的值要大于0,防止越界
{
if(*(str1 + i1) > *(str2 + i2)) //*(str1 + i1)大于*(str2 + i2)时,将*(str1 + i1)的值赋值到*(dest + j)
{
*(dest + j) = *(str1 + i1);
i1--; //i1减减,找到数组arr1的上一个元素
j--; //j减减,继续覆盖元素
}
else
{
*(dest + j) = *(str2 + i2); //*(str2 + i2)大于*(str1 + i1)时,或者*(str2 + i2)等于*(str1 + i1)时(复制哪个值都可以),将*(str2 + i2)的值赋值到*(dest + j)
i2--; //i1减减,找到数组arr2的上一个元素
j--; //j减减,继续覆盖元素
}
}
while(i2 >= 0) //i1没有遍历完没关系,因为就是要覆盖到数组arr1,要保证i2遍历完
{
*(dest + j) = *(str2 + i2);
i2--;
j--;
}
print(arr1,len1);
return 0;
}
运行结果如下:

由运行结果可以得知,此串代码符合我们的要求。
这串代码的时间复杂度:O(N)
空间复杂度:O(1)
今天,对于指针讲解就到处结束了,指针是非常重要的东西,特别是后面数据结构的学习中,指针更是频繁使用,所以对于指针掌握要求应当更高。
关注点一点,下期更精彩。





![[TCP/IP] Linux 搭建服务器局域网](https://img-blog.csdnimg.cn/5525d683a64a4d0085fc13319ef127d0.png#pic_center)