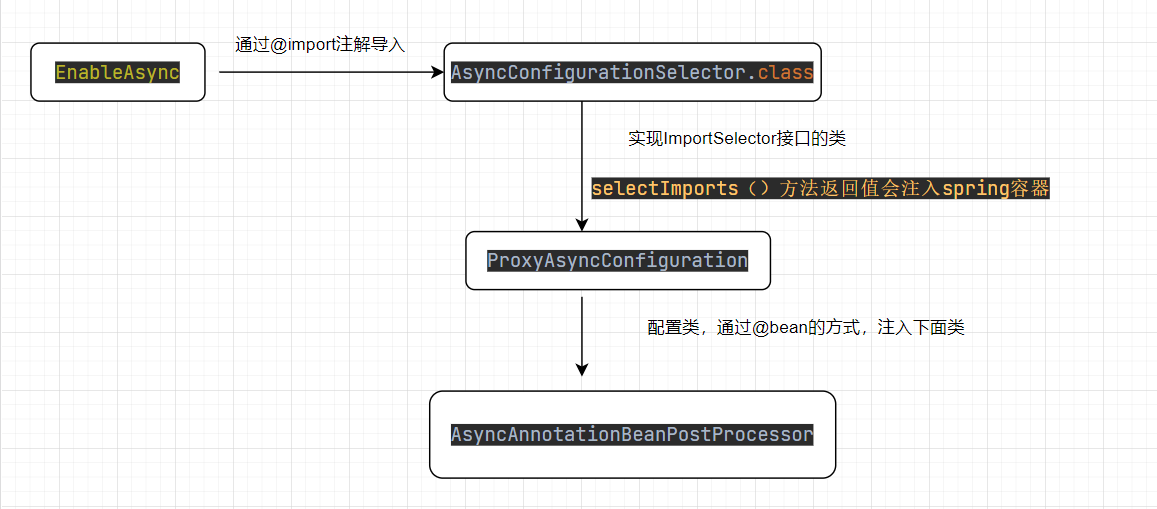
T:what
Y:why
W:how
Y
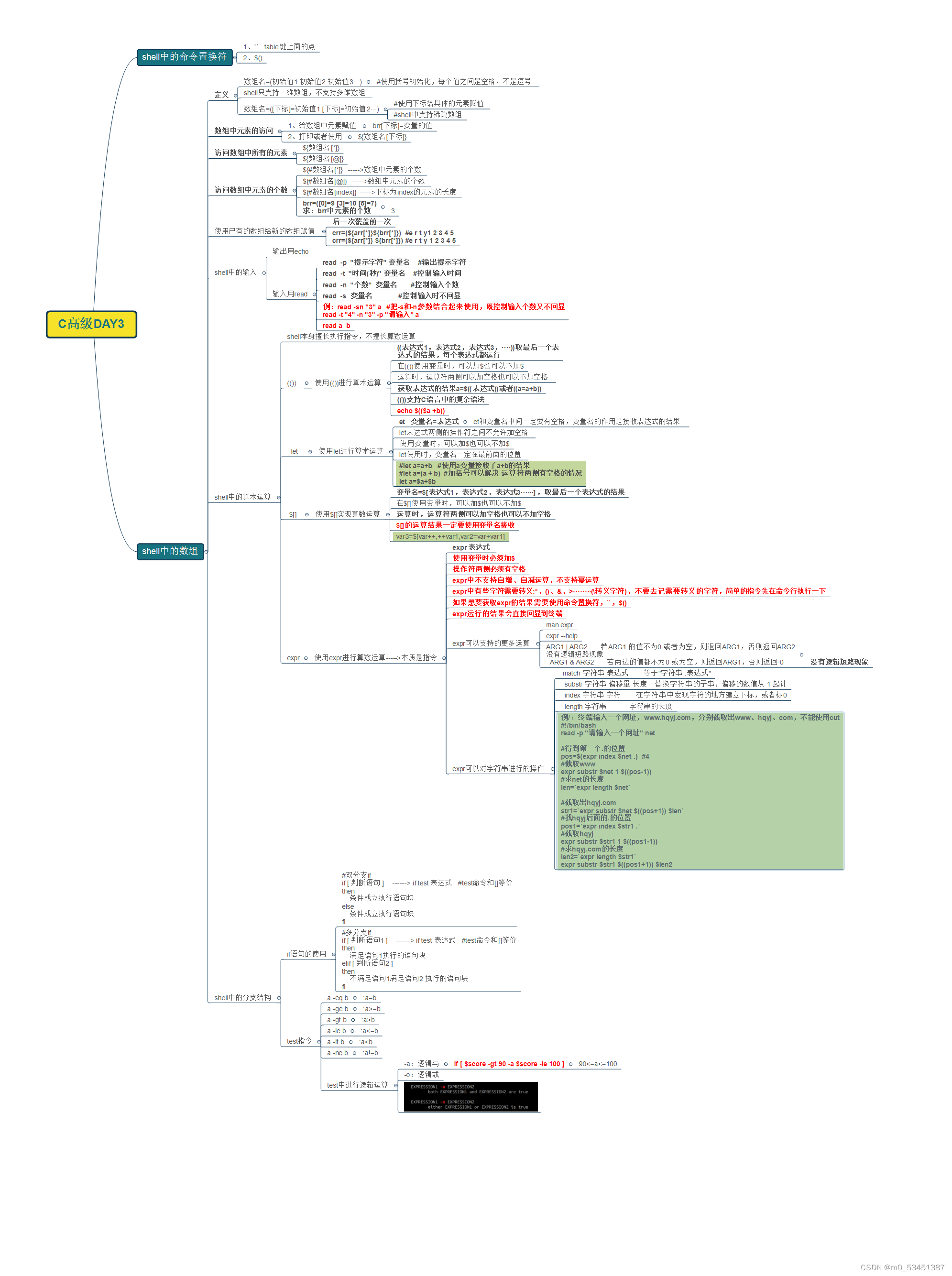
针对点云的无序性,无法通过坐标索引进行查询,常常将点云地图转换其他类型的地图,如Octomap,从而进行碰撞检测;
W
为快速进行机器人与障碍物的位置计算,可以采用凸包算法获取一个包含点云的凸包,如PCL库中CropHull滤波器,得到凸包后可以向上一问中那样获取机器人与障碍物之间的位置关系,如下图所示,如果机器人是凸多边形描述,也可使用GJK-EPA检测凸多边形之间的碰撞。
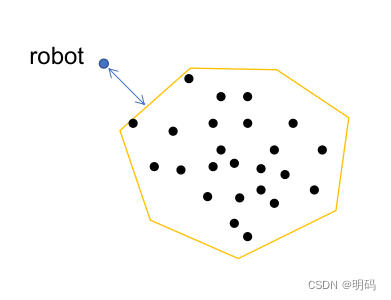
针对点云进行经过完整凸包处理后计算最短距离固然方便,但由于需要对点云进行预处理,增加了碰撞检测算法的计算复杂度,特别对于高维情况更是如此。
其实可以直接对障碍物点云与自由空间进行分割,将对模长最小碰撞向量的求取转化为求一个分离超平面,如下图黑色虚线所示
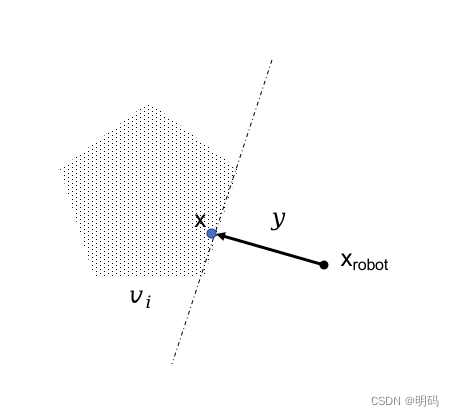
设碰撞向量为
x
−
x
robot
=
y
x-x_{\text {robot }}=y
x−xrobot =y,y满足机器人与点云向量在y上的投影需要大于y的模长,并要求机器人距离这个超平面的距离尽可能长,即如下优化问题
max y ∈ R 2 y T y s.t. ( v i − x robot ) T y ≥ y T y , ∀ i ∈ { 1 , … , m } \begin{array}{l}\max _{y \in {R}^{\mathrm{2}}} y^{\mathrm{T}} y \\ \text { s.t. }\left(v_{i}-x_{\text {robot }}\right)^{\mathrm{T}} y \geq y^{\mathrm{T}} y, \forall i \in\{1, \ldots, m\}\end{array} maxy∈R2yTy s.t. (vi−xrobot )Ty≥yTy,∀i∈{1,…,m}
通过极对偶变换,转化为凸问题,令
z
=
y
/
(
y
T
y
)
z=y /\left(y^{\mathrm{T}} y\right)
z=y/(yTy)
min
z
∈
R
2
z
T
z
s.t.
(
v
i
−
x
robot
)
T
z
≥
1
,
∀
i
∈
{
1
,
…
,
m
}
\begin{array}{l}\min _{z \in{R}^{2}} z^{\mathrm{T}} z \\ \text { s.t. }\left(v_{i}-x_{\text {robot }}\right)^{\mathrm{T}} z \geq 1, \forall i \in\{1, \ldots, m\}\end{array}
minz∈R2zTz s.t. (vi−xrobot )Tz≥1,∀i∈{1,…,m}
从而转化为QP问题进行求解,可得x为
x
=
z
/
(
z
T
z
)
+
x
robot
x=z /\left(z^{\mathrm{T}} z\right)+x_{\text {robot }}
x=z/(zTz)+xrobot
如图为rviz仿真图像,其中红色表示点云,绿色marker表示机器人,蓝色箭头表示碰撞向量,可以看到距离分离超平面的最短距离为蓝色箭头的长度

3维度情况

[项目开源地址] 待完善
ref
Rockafellar RT. A dual approach to solving nonlinear programming problems by unconstrained optimization.Mathematical Programming. 1973 Dec;5(1):354-73.
Seidel R. Small-dimensional linear programming and convex hulls made easy. Discrete & Computational Geometry. 1991 Sep;6(3):423-34.
https://www.shenlanxueyuan.com/course/573/task/21138/show